tf
Transfer function model
Description
Use tf to create real-valued or complex-valued transfer
function models, or to convert dynamic system
models to transfer function form.
Transfer functions are a frequency-domain representation of linear time-invariant
systems. For instance, consider a continuous-time SISO dynamic system represented by the
transfer function sys(s) = N(s)/D(s), where s = jw
and N(s) and D(s) are called the numerator and
denominator polynomials, respectively. The tf model object can
represent SISO or MIMO transfer functions in continuous time or discrete time.
You can create a transfer function model object either by specifying its coefficients
directly, or by converting a model of another type (such as a state-space model
ss) to transfer-function form. For more information, see Transfer Functions.
You can also use tf to create generalized state-space (genss) models or uncertain state-space (uss (Robust Control Toolbox)) models.
Creation
Syntax
Description
sys = tf(numerator,denominator)Numerator and Denominator
properties. For instance, consider a continuous-time SISO dynamic system
represented by the transfer function sys(s) = N(s)/D(s),
the input arguments numerator and
denominator are the coefficients of
N(s) and D(s),
respectively.
sys = tf(numerator,denominator,ts)Numerator, Denominator, and
Ts properties. For instance, consider a
discrete-time SISO dynamic system represented by the transfer function
sys(z) = N(z)/D(z), the input arguments
numerator and denominator are
the coefficients of N(z) and D(z),
respectively. To leave the sample time unspecified, set
ts input argument to -1.
sys = tf(numerator,denominator,ltiSys)ltiSys, including the sample time.
s = tf('s') creates special variable
s that you can use in a rational expression to create
a continuous-time transfer function model. Using a rational expression can
sometimes be easier and more intuitive than specifying polynomial
coefficients.
Input Arguments
numerator — Numerator coefficients of the transfer function
row vector | Ny-by-Nu cell array of row
vectors
Numerator coefficients of the transfer function, specified as:
A row vector of polynomial coefficients.
An
Ny-by-Nucell array of row vectors to specify a MIMO transfer function, whereNyis the number of outputs, andNuis the number of inputs.
When you create the transfer function, specify the numerator
coefficients in order of descending power. For instance, if the transfer
function numerator is 3s^2-4s+5, then specify
numerator as [3 -4 5]. For a
discrete-time transfer function with numerator 2z-1,
set numerator to [2 -1].
Also a property of the tf object. For more
information, see Numerator.
denominator — Denominator coefficients of the transfer function
row vector | Ny-by-Nu cell array of row
vectors
Denominator coefficients, specified as:
A row vector of polynomial coefficients.
An
Ny-by-Nucell array of row vectors to specify a MIMO transfer function, whereNyis the number of outputs andNuis the number of inputs.
When you create the transfer function, specify the denominator
coefficients in order of descending power. For instance, if the transfer
function denominator is 7s^2+8s-9, then specify
denominator as [7 8 -9]. For
a discrete-time transfer function with denominator
2z^2+1, set denominator to
[2 0 1].
Also a property of the tf object. For more
information, see Denominator.
ts — Sample time
scalar
Sample time, specified as a scalar. Also a property of the
tf object. For more information, see Ts.
ltiSys — Dynamic system
dynamic system model | model array
Dynamic system, specified as a SISO or MIMO dynamic system model or array of dynamic system models. Dynamic systems that you can use include:
Continuous-time or discrete-time numeric LTI models, such as
tf,zpk,ss, orpidmodels.Generalized or uncertain LTI models such as
genssoruss(Robust Control Toolbox) models. (Using uncertain models requires Robust Control Toolbox™ software.)The resulting transfer function assumes
current values of the tunable components for tunable control design blocks.
nominal model values for uncertain control design blocks.
Identified LTI models, such as
idtf(System Identification Toolbox),idss(System Identification Toolbox),idproc(System Identification Toolbox),idpoly(System Identification Toolbox), andidgrey(System Identification Toolbox) models. To select the component of the identified model to convert, specifycomponent. If you do not specifycomponent,tfconverts the measured component of the identified model by default. (Using identified models requires System Identification Toolbox™ software.)
m — Static gain
scalar | matrix
Static gain, specified as a scalar or matrix. Static gain or steady state gain of a system represents the ratio of the output to the input under steady state condition.
component — Component of identified model
'measured' (default) | 'noise' | 'augmented'
Component of identified model to convert, specified as one of the following:
'measured'— Convert the measured component ofsys.'noise'— Convert the noise component ofsys'augmented'— Convert both the measured and noise components ofsys.
component only applies when
sys is an identified LTI model.
For more information on identified LTI models and their measured and noise components, see Identified LTI Models.
Output Arguments
sys — Output system model
tf model object | genss model object | uss model object
Output system model, returned as:
A transfer function (
tf) model object, whennumeratoranddenominatorinput arguments are numeric arrays.A generalized state-space model (
genss) object, when thenumeratorordenominatorinput arguments includes tunable parameters, such asrealpparameters or generalized matrices (genmat). For an example, see Tunable Low-Pass Filter.An uncertain state-space model (
uss) object, when thenumeratorordenominatorinput arguments includes uncertain parameters. Using uncertain models requires Robust Control Toolbox software. For an example, see Transfer Function with Uncertain Coefficients (Robust Control Toolbox).
Properties
Numerator — Numerator coefficients
row vector | Ny-by-Nu cell array of row
vectors
Numerator coefficients, specified as:
A row vector of polynomial coefficients in order of descending power (for
Variablevalues's','z','p', or'q') or in order of ascending power (forVariablevalues'z^-1'or'q^-1').An
Ny-by-Nucell array of row vectors to specify a MIMO transfer function, whereNyis the number of outputs andNuis the number of inputs. Each element of the cell array specifies the numerator coefficients for a given input/output pair. If you specify bothNumeratorandDenominatoras cell arrays, they must have the same dimensions.
The coefficients of Numerator can be either
real-valued or complex-valued.
Denominator — Denominator coefficients
row vector | Ny-by-Nu cell array of row
vectors
Denominator coefficients, specified as:
A row vector of polynomial coefficients in order of descending power (for values
Variablevalues's','z','p', or'q') or in order of ascending power (forVariablevalues'z^-1'or'q^-1').An
Ny-by-Nucell array of row vectors to specify a MIMO transfer function, whereNyis the number of outputs andNuis the number of inputs. Each element of the cell array specifies the numerator coefficients for a given input/ output pair. If you specify bothNumeratorandDenominatoras cell arrays, they must have the same dimensions.
If all SISO entries of a MIMO transfer function have the same denominator,
you can specify Denominator as the row vector while
specifying Numerator as a cell array.
The coefficients of Denominator can be either
real-valued or complex-valued.
Variable — Transfer function display variable
's' (default) | 'z' | 'p' | 'q' | 'z^-1' | 'q^-1'
Transfer function display variable, specified as one of the following:
's'— Default for continuous-time models'z'— Default for discrete-time models'p'— Equivalent to's''q'— Equivalent to'z''z^-1'— Inverse of'z''q^-1'— Equivalent to'z^-1'
The value of Variable is reflected in the display, and
also affects the interpretation of the Numerator and
Denominator coefficient vectors for discrete-time
models.
For
Variablevalues's','z','p', or'q', the coefficients are ordered in descending powers of the variable. For example, consider the row vector[ak ... a1 a0]. The polynomial order is specified as .For
Variablevalues'z^-1'or'q^-1', the coefficients are ordered in ascending powers of the variable. For example, consider the row vector[b0 b1 ... bk]. The polynomial order is specified as .
For examples, see Specify Polynomial Ordering in Discrete-Time Transfer Function, Transfer Function Model Using Rational Expression, and Discrete-Time Transfer Function Model Using Rational Expression.
IODelay — Transport delay
0 (default) | scalar | Ny-by-Nu array
Transport delay, specified as one of the following:
Scalar — Specify the transport delay for a SISO system or the same transport delay for all input/output pairs of a MIMO system.
Ny-by-Nuarray — Specify separate transport delays for each input/output pair of a MIMO system. Here,Nyis the number of outputs andNuis the number of inputs.
For continuous-time systems, specify transport delays in the time unit
specified by the TimeUnit property. For discrete-time
systems, specify transport delays in integer multiples of the sample time,
Ts.
InputDelay — Input delay
0 (default) | scalar | Nu-by-1 vector
Input delay for each input channel, specified as one of the following:
Scalar — Specify the input delay for a SISO system or the same delay for all inputs of a multi-input system.
Nu-by-1 vector — Specify separate input delays for input of a multi-input system, whereNuis the number of inputs.
For continuous-time systems, specify input delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify input delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
OutputDelay — Output delay
0 (default) | scalar | Ny-by-1 vector
Output delay for each output channel, specified as one of the following:
Scalar — Specify the output delay for a SISO system or the same delay for all outputs of a multi-output system.
Ny-by-1 vector — Specify separate output delays for output of a multi-output system, whereNyis the number of outputs.
For continuous-time systems, specify output delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify output delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
Ts — Sample time
0 (default) | positive scalar | -1
Sample time, specified as:
0for continuous-time systems.A positive scalar representing the sampling period of a discrete-time system. Specify
Tsin the time unit specified by theTimeUnitproperty.-1for a discrete-time system with an unspecified sample time.
TimeUnit — Time variable units
'seconds' (default) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...
Time variable units, specified as one of the following:
'nanoseconds''microseconds''milliseconds''seconds''minutes''hours''days''weeks''months''years'
Changing TimeUnit has no effect on other properties, but changes the overall system behavior. Use chgTimeUnit to convert between time units without modifying system behavior.
InputName — Input channel names
'' (default) | character vector | cell array of character vectors
Input channel names, specified as one of the following:
A character vector, for single-input models.
A cell array of character vectors, for multi-input models.
'', no names specified, for any input channels.
Alternatively, you can assign input names for multi-input models using automatic vector
expansion. For example, if sys is a two-input model, enter the
following:
sys.InputName = 'controls';The input names automatically expand to {'controls(1)';'controls(2)'}.
You can use the shorthand notation u to refer to the InputName property. For example, sys.u is equivalent to sys.InputName.
Use InputName to:
Identify channels on model display and plots.
Extract subsystems of MIMO systems.
Specify connection points when interconnecting models.
InputUnit — Input channel units
'' (default) | character vector | cell array of character vectors
Input channel units, specified as one of the following:
A character vector, for single-input models.
A cell array of character vectors, for multi-input models.
'', no units specified, for any input channels.
Use InputUnit to specify input signal units. InputUnit has no effect on system behavior.
InputGroup — Input channel groups
structure
Input channel groups, specified as a structure. Use InputGroup to assign
the input channels of MIMO systems into groups and refer to each group by name. The
field names of InputGroup are the group names and the field values
are the input channels of each group. For example, enter the following to create input
groups named controls and noise that include input
channels 1 and 2, and 3 and
5, respectively.
sys.InputGroup.controls = [1 2]; sys.InputGroup.noise = [3 5];
You can then extract the subsystem from the controls inputs to all outputs
using the following.
sys(:,'controls')By default, InputGroup is a structure with no fields.
OutputName — Output channel names
'' (default) | character vector | cell array of character vectors
Output channel names, specified as one of the following:
A character vector, for single-output models.
A cell array of character vectors, for multi-output models.
'', no names specified, for any output channels.
Alternatively, you can assign output names for multi-output models using automatic vector
expansion. For example, if sys is a two-output model, enter the
following.
sys.OutputName = 'measurements';The output names automatically expand to {'measurements(1)';'measurements(2)'}.
You can also use the shorthand notation y to refer to the OutputName property. For example, sys.y is equivalent to sys.OutputName.
Use OutputName to:
Identify channels on model display and plots.
Extract subsystems of MIMO systems.
Specify connection points when interconnecting models.
OutputUnit — Output channel units
'' (default) | character vector | cell array of character vectors
Output channel units, specified as one of the following:
A character vector, for single-output models.
A cell array of character vectors, for multi-output models.
'', no units specified, for any output channels.
Use OutputUnit to specify output signal units. OutputUnit has no effect on system behavior.
OutputGroup — Output channel groups
structure
Output channel groups, specified as a structure. Use OutputGroupto assign
the output channels of MIMO systems into groups and refer to each group by name. The
field names of OutputGroup are the group names and the field values
are the output channels of each group. For example, create output groups named
temperature and measurement that include
output channels 1, and 3 and 5,
respectively.
sys.OutputGroup.temperature = [1]; sys.OutputGroup.measurement = [3 5];
You can then extract the subsystem from all inputs to the measurement
outputs using the following.
sys('measurement',:)By default, OutputGroup is a structure with no fields.
Name — System name
'' (default) | character vector
System name, specified as a character vector. For example, 'system_1'.
Notes — User-specified text
{} (default) | character vector | cell array of character vectors
User-specified text that you want to associate with the system, specified as a character vector or cell array of character vectors. For example, 'System is MIMO'.
UserData — User-specified data
[] (default) | any MATLAB® data type
User-specified data that you want to associate with the system, specified as any MATLAB data type.
SamplingGrid — Sampling grid for model arrays
structure array
Sampling grid for model arrays, specified as a structure array.
Use SamplingGrid to track the variable values associated with each model in a model array, including identified linear time-invariant (IDLTI) model arrays.
Set the field names of the structure to the names of the sampling variables. Set the field values to the sampled variable values associated with each model in the array. All sampling variables must be numeric scalars, and all arrays of sampled values must match the dimensions of the model array.
For example, you can create an 11-by-1 array of linear models, sysarr, by taking snapshots of a linear time-varying system at times t = 0:10. The following code stores the time samples with the linear models.
sysarr.SamplingGrid = struct('time',0:10)Similarly, you can create a 6-by-9 model array, M, by independently sampling two variables, zeta and w. The following code maps the (zeta,w) values to M.
[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>) M.SamplingGrid = struct('zeta',zeta,'w',w)
When you display M, each entry in the array includes the corresponding zeta and w values.
M
M(:,:,1,1) [zeta=0.3, w=5] =
25
--------------
s^2 + 3 s + 25
M(:,:,2,1) [zeta=0.35, w=5] =
25
----------------
s^2 + 3.5 s + 25
...For model arrays generated by linearizing a Simulink® model at multiple parameter values or operating points, the software populates SamplingGrid automatically with the variable values that correspond to each entry in the array. For instance, the Simulink
Control Design™ commands linearize (Simulink Control Design) and slLinearizer (Simulink Control Design) populate SamplingGrid automatically.
By default, SamplingGrid is a structure with no fields.
Object Functions
The following lists contain a representative subset of the functions you can use with
tf models. In general, any function applicable to Dynamic System Models
is applicable to a tf object.
Linear Analysis
step | Step response of dynamic system |
impulse | Impulse response plot of dynamic system; impulse response data |
lsim | Plot simulated time response of dynamic system to arbitrary inputs; simulated response data |
bode | Bode plot of frequency response, or magnitude and phase data |
nyquist | Nyquist plot of frequency response |
nichols | Nichols chart of frequency response |
bandwidth | Frequency response bandwidth |
Stability Analysis
Model Transformation
Model Interconnection
Examples
SISO Transfer Function Model
For this example, consider the following SISO transfer function model:
Specify the numerator and denominator coefficients ordered in descending powers of s, and create the transfer function model.
numerator = 1; denominator = [2,3,4]; sys = tf(numerator,denominator)
sys =
1
---------------
2 s^2 + 3 s + 4
Continuous-time transfer function.
Discrete-Time SISO Transfer Function Model
For this example, consider the following discrete-time SISO transfer function model:
Specify the numerator and denominator coefficients ordered in descending powers of z and the sample time of 0.1 seconds. Create the discrete-time transfer function model.
numerator = [2,0]; denominator = [4,0,3,-1]; ts = 0.1; sys = tf(numerator,denominator,ts)
sys =
2 z
---------------
4 z^3 + 3 z - 1
Sample time: 0.1 seconds
Discrete-time transfer function.
Second-Order Transfer Function from Damping Ratio and Natural Frequency
For this example, consider a transfer function model that represents a second-order system with known natural frequency and damping ratio.
The transfer function of a second-order system, expressed in terms of its damping ratio and natural frequency , is:
Assuming a damping ratio, = 0.25 and natural frequency, = 3 rad/s, create the second order transfer function.
zeta = 0.25; w0 = 3; numerator = w0^2; denominator = [1,2*zeta*w0,w0^2]; sys = tf(numerator,denominator)
sys =
9
---------------
s^2 + 1.5 s + 9
Continuous-time transfer function.
Examine the response of this transfer function to a step input.
stepplot(sys)
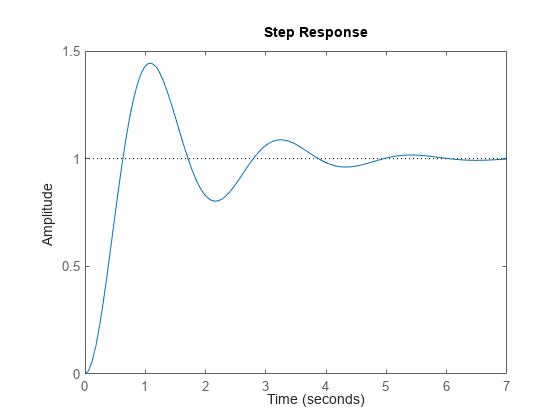
The plot shows the ringdown expected of a second-order system with a low damping ratio.
Discrete-Time MIMO Transfer Function Model
Create a transfer function for the discrete-time, multi-input, multi-output model:
with sample time ts = 0.2 seconds.
Specify the numerator coefficients as a 2-by-2 matrix.
numerators = {1 [1 0];[-1 2] 3};Specify the coefficients of the common denominator as a row vector.
denominator = [1 0.3];
Create the discrete-time MIMO transfer function model.
ts = 0.2; sys = tf(numerators,denominator,ts)
sys =
From input 1 to output...
1
1: -------
z + 0.3
-z + 2
2: -------
z + 0.3
From input 2 to output...
z
1: -------
z + 0.3
3
2: -------
z + 0.3
Sample time: 0.2 seconds
Discrete-time transfer function.
For more information on creating MIMO transfer functions, see MIMO Transfer Functions.
Concatenate SISO Transfer Functions into MIMO Transfer Function Model
In this example, you create a MIMO transfer function model by concatenating SISO transfer function models. Consider the following single-input, two-output transfer function:
Specify the MIMO transfer function model by concatenating the SISO entries.
sys1 = tf([1 -1],[1 1]); sys2 = tf([1 2],[1 4 5]); sys = [sys1;sys2]
sys =
From input to output...
s - 1
1: -----
s + 1
s + 2
2: -------------
s^2 + 4 s + 5
Continuous-time transfer function.
For more information on creating MIMO transfer functions, see MIMO Transfer Functions.
Transfer Function Model Using Rational Expression
For this example, create a continuous-time transfer function model using rational expressions. Using a rational expression can sometimes be easier and more intuitive than specifying polynomial coefficients of the numerator and denominator.
Consider the following system:
To create the transfer function model, first specify s as a tf object.
s = tf('s')s = s Continuous-time transfer function.
Create the transfer function model using s in the rational expression.
sys = s/(s^2 + 2*s + 10)
sys =
s
--------------
s^2 + 2 s + 10
Continuous-time transfer function.
Discrete-Time Transfer Function Model Using Rational Expression
For this example, create a discrete-time transfer function model using a rational expression. Using a rational expression can sometimes be easier and more intuitive than specifying polynomial coefficients.
Consider the following system:
To create the transfer function model, first specify z as a tf object and the sample time Ts.
ts = 0.1;
z = tf('z',ts)z = z Sample time: 0.1 seconds Discrete-time transfer function.
Create the transfer function model using z in the rational expression.
sys = (z - 1) / (z^2 - 1.85*z + 0.9)
sys =
z - 1
------------------
z^2 - 1.85 z + 0.9
Sample time: 0.1 seconds
Discrete-time transfer function.
Transfer Function Model with Inherited Properties
For this example, create a transfer function model with properties inherited from another transfer function model. Consider the following two transfer functions:
For this example, create sys1 with the TimeUnit and InputDelay property set to 'minutes'.
numerator1 = [2,0]; denominator1 = [1,8,0]; sys1 = tf(numerator1,denominator1,'TimeUnit','minutes','InputUnit','minutes')
sys1 =
2 s
---------
s^2 + 8 s
Continuous-time transfer function.
propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1x2 cell
{'minutes'} {'minutes'}
Create the second transfer function model with properties inherited from sys1.
numerator2 = [1,-1]; denominator2 = [7,2,0,0,9]; sys2 = tf(numerator2,denominator2,sys1)
sys2 =
s - 1
-----------------
7 s^4 + 2 s^3 + 9
Continuous-time transfer function.
propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1x2 cell
{'minutes'} {'minutes'}
Observe that the transfer function model sys2 has that same properties as sys1.
Array of Transfer Function Models
You can use a for loop to specify an array of transfer function models.
First, pre-allocate the transfer function array with zeros.
sys = tf(zeros(1,1,3));
The first two indices represent the number of outputs and inputs for the models, while the third index is the number of models in the array.
Create the transfer function model array using a rational expression in the for loop.
s = tf('s'); for k = 1:3 sys(:,:,k) = k/(s^2+s+k); end sys
sys(:,:,1,1) =
1
-----------
s^2 + s + 1
sys(:,:,2,1) =
2
-----------
s^2 + s + 2
sys(:,:,3,1) =
3
-----------
s^2 + s + 3
3x1 array of continuous-time transfer functions.
Convert State-Space Model to Transfer Function
For this example, compute the transfer function of the following state-space model:
Create the state-space model using the state-space matrices.
A = [-2 -1;1 -2]; B = [1 1;2 -1]; C = [1 0]; D = [0 1]; ltiSys = ss(A,B,C,D);
Convert the state-space model ltiSys to a transfer function.
sys = tf(ltiSys)
sys =
From input 1 to output:
s
-------------
s^2 + 4 s + 5
From input 2 to output:
s^2 + 5 s + 8
-------------
s^2 + 4 s + 5
Continuous-time transfer function.
Extract Transfer Functions from Identified Model
For this example, extract the measured and noise components of an identified polynomial model into two separate transfer functions.
Load the Box-Jenkins polynomial model ltiSys in identifiedModel.mat.
load('identifiedModel.mat','ltiSys');
ltiSys is an identified discrete-time model of the form: , where represents the measured component and the noise component.
Extract the measured and noise components as transfer functions.
sysMeas = tf(ltiSys,'measured') sysMeas =
From input "u1" to output "y1":
-0.1426 z^-1 + 0.1958 z^-2
z^(-2) * ----------------------------
1 - 1.575 z^-1 + 0.6115 z^-2
Sample time: 0.04 seconds
Discrete-time transfer function.
sysNoise = tf(ltiSys,'noise')sysNoise =
From input "v@y1" to output "y1":
0.04556 + 0.03301 z^-1
----------------------------------------
1 - 1.026 z^-1 + 0.26 z^-2 - 0.1949 z^-3
Input groups:
Name Channels
Noise 1
Sample time: 0.04 seconds
Discrete-time transfer function.
The measured component can serve as a plant model, while the noise component can be used as a disturbance model for control system design.
Specify Input and Output Names for MIMO Transfer Function Model
Transfer function model objects include model data that helps you keep track of what the model represents. For instance, you can assign names to the inputs and outputs of your model.
Consider the following continuous-time MIMO transfer function model:
The model has one input Current, and two outputs Torque and Angular velocity.
First, specify the numerator and denominator coefficients of the model.
numerators = {[1 1] ; 1};
denominators = {[1 2 2] ; [1 0]};Create the transfer function model, specifying the input name and output names.
sys = tf(numerators,denominators,'InputName','Current',... 'OutputName',{'Torque' 'Angular Velocity'})
sys =
From input "Current" to output...
s + 1
Torque: -------------
s^2 + 2 s + 2
1
Angular Velocity: -
s
Continuous-time transfer function.
Specify Polynomial Ordering in Discrete-Time Transfer Function
For this example, specify polynomial ordering in discrete-time transfer function models using the 'Variable' property.
Consider the following discrete-time transfer functions with sample time 0.1 seconds:
Create the first discrete-time transfer function by specifying the z coefficients.
numerator = [1,0,0]; denominator = [1,2,3]; ts = 0.1; sys1 = tf(numerator,denominator,ts)
sys1 =
z^2
-------------
z^2 + 2 z + 3
Sample time: 0.1 seconds
Discrete-time transfer function.
The coefficients of sys1 are ordered in descending powers of z.
tf switches convention based on the value of the 'Variable' property. Since sys2 is the inverse transfer function model of sys1, specify 'Variable' as 'z^-1' and use the same numerator and denominator coefficients.
sys2 = tf(numerator,denominator,ts,'Variable','z^-1')
sys2 =
1
-------------------
1 + 2 z^-1 + 3 z^-2
Sample time: 0.1 seconds
Discrete-time transfer function.
The coefficients of sys2 are now ordered in ascending powers of z^-1.
Based on different conventions, you can specify polynomial ordering in transfer function models using the 'Variable' property.
Tunable Low-Pass Filter
In this example, you will create a low-pass filter with one tunable parameter a:
Since the numerator and denominator coefficients of a tunableTF block are independent, you cannot use tunableTF to represent F. Instead, construct F using the tunable real parameter object realp.
Create a real tunable parameter with an initial value of 10.
a = realp('a',10)a =
Name: 'a'
Value: 10
Minimum: -Inf
Maximum: Inf
Free: 1
Real scalar parameter.
Use tf to create the tunable low-pass filter F.
numerator = a; denominator = [1,a]; F = tf(numerator,denominator)
Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks: a: Scalar parameter, 2 occurrences. Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.
F is a genss object which has the tunable parameter a in its Blocks property. You can connect F with other tunable or numeric models to create more complex control system models. For an example, see Control System with Tunable Components.
Static Gain MIMO Transfer Function Model
In this example, you will create a static gain MIMO transfer function model.
Consider the following two-input, two-output static gain matrix m:
Specify the gain matrix and create the static gain transfer function model.
m = [2,4;...
3,5];
sys1 = tf(m)sys1 = From input 1 to output... 1: 2 2: 3 From input 2 to output... 1: 4 2: 5 Static gain.
You can use static gain transfer function model sys1 obtained above to cascade it with another transfer function model.
For this example, create another two-input, two-output discrete transfer function model and use the series function to connect the two models.
numerators = {1,[1,0];[-1,2],3};
denominator = [1,0.3];
ts = 0.2;
sys2 = tf(numerators,denominator,ts)sys2 =
From input 1 to output...
1
1: -------
z + 0.3
-z + 2
2: -------
z + 0.3
From input 2 to output...
z
1: -------
z + 0.3
3
2: -------
z + 0.3
Sample time: 0.2 seconds
Discrete-time transfer function.
sys = series(sys1,sys2)
sys =
From input 1 to output...
3 z^2 + 2.9 z + 0.6
1: -------------------
z^2 + 0.6 z + 0.09
-2 z^2 + 12.4 z + 3.9
2: ---------------------
z^2 + 0.6 z + 0.09
From input 2 to output...
5 z^2 + 5.5 z + 1.2
1: -------------------
z^2 + 0.6 z + 0.09
-4 z^2 + 21.8 z + 6.9
2: ---------------------
z^2 + 0.6 z + 0.09
Sample time: 0.2 seconds
Discrete-time transfer function.
Limitations
Transfer function models are ill-suited for numerical computations. Once created, convert them to state-space form before combining them with other models or performing model transformations. You can then convert the resulting models back to transfer function form for inspection purposes
An identified nonlinear model cannot be directly converted into a transfer function model using
tf. To obtain a transfer function model:Convert the nonlinear identified model to an identified LTI model using
linapp(System Identification Toolbox),idnlarx/linearize(System Identification Toolbox), oridnlhw/linearize(System Identification Toolbox).Then, convert the resulting model to a transfer function model using
tf.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)