Convolution
Convolution of two inputs
Libraries:
DSP System Toolbox /
Signal Operations
Description
The Convolution block convolves the first dimension of an N-D input array u with the first dimension of an N-D input array v. The block can also convolve a column vector with the first-dimension of an N-D input array.
The general equation for convolution is:
Two DSP System Toolbox™ blocks can be used for convolving two input signals:
Convolution
Discrete FIR Filter (Simulink)
The Convolution block assumes that all elements of u and v are available at each Simulink® time step and computes the entire convolution at every step.
The Discrete FIR Filter block can be used for convolving signals in situations where all elements of v is available at each time step, but u is a sequence that comes in over the life of the simulation. When you use the Discrete FIR Filter block, the convolution is computed only once.
To determine which block best fits your needs, see Selecting the Appropriate Convolution Block.
Examples
Ports
Input
Port_1 — First input signal
scalar | vector | matrix | N-D array
First input u specified as a scalar, vector, matrix, or N-D array. When both inputs are real, the output is real. When one or both inputs are complex, the output is complex. All the input port dimensions for both the inputs, except the first dimension, must have the same value.
Inputs u and v are zero when indexed outside their valid ranges.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Port_2 — Second input signal
scalar | vector | matrix | N-D array
Second input v specified as a scalar, vector, matrix, or N-D array. When both inputs are real, the output is real. When one or both inputs are complex, the output is complex. All the input port dimensions for both the inputs, except the first dimension, must have the same value.
Inputs u and v are zero when indexed outside their valid ranges.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Output
Port_1 — Output signal
scalar | vector | matrix | N-D array
Convolved signal, returned as a scalar, vector, matrix, or N-D array depending on the input signals. When both inputs are real, the output is real. When one or both inputs are complex, the output is complex. Inputs u and v are zero when indexed outside of their valid ranges. For more details on how the convolved signal changes based on the inputs, see More About.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Parameters
Main Tab
Computation domain — Computation domain
Time (default) | Frequency | Fastest
Set the domain in which the block computes convolutions:
Time— The block computes in the time domain, which minimizes memory use.Frequency— The block computes in the frequency domain, which might require fewer computations than computing in the time domain, depending on the input length.Fastest— The block computes in the domain that minimizes the number of computations.
Fixed-point signals are only supported in the time domain. When
inputting fixed-point signals, make sure you set the
Computation domain parameter to
Time.
Data Types Tab
Rounding mode — Method of rounding operation
Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero
Specify the rounding mode for fixed-point operations as one of the following:
FloorCeilingConvergentNearestRoundSimplestZero
For more details, see Rounding Modes.
Note
The Rounding mode and Saturate on integer overflow parameters have no effect on numerical results when all these conditions are met:
Product output data type is
Inherit: Inherit via internal rule.Accumulator data type is
Inherit: Inherit via internal rule.Output data type is
Inherit: Same as accumulator.
With these data-type settings, the block operates in a full-precision mode.
Saturate on integer overflow — Method of overflow action
off (default) | on
When you select this parameter, the block saturates the result of its fixed-point operation. When you clear this parameter, the block wraps the result of its fixed-point operation. For details on saturate and wrap, see Overflow Handing for fixed-point operations.
Note
The Rounding mode and Saturate on integer overflow parameters have no effect on numerical results when all these conditions are met:
Product output data type is
Inherit: Inherit via internal rule.Accumulator data type is
Inherit: Inherit via internal rule.Output data type is
Inherit: Same as accumulator.
With these data-type settings, the block operates in a full-precision mode.
Product output — Product output data type
Inherit: Inherit via internal
rule (default) | Inherit: Same as first input | fixdt([],16,0)
Product output specifies the data type of the output of a product operation in the Convolution block.
Inherit: Inherit via internal rule— The block inherits the product output data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.Inherit: Same as first input— The block specifies the product output data type to be the same as the first input data type.fixdt([],16,0)— The block specifies an autosigned, binary-point, scaled, fixed-point data type with a word length of 16 bits and a fraction length of 0.
Alternatively, you can set the Product output
data type by using the Data Type Assistant. To use
the assistant, click the Show data type assistant
button![]() .
.
For more information on the data type assistant, see Specify Data Types Using Data Type Assistant (Simulink).
For more information on the product output data type, see Multiplication Data Types and Fixed-Point Data Types.
Accumulator — Data type of accumulator
Inherit: Inherit via internal
rule (default) | Inherit: Same as first input | Inherit: Same as product output | fixdt([],16,0)
Accumulator specifies the data type of the output of an accumulation operation in the Convolution block.
Inherit: Inherit via internal rule— The block inherits the accumulator data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.Inherit: Same as first input— The block specifies the accumulator data type to be the same as the first input data type.Inherit: Same as product output— The block specifies the accumulator data type to be the same as the product output data type.fixdt([],16,0)— The block specifies an autosigned, binary-point, scaled, fixed-point data type with a word length of 16 bits and a fraction length of 0.
Alternatively, you can set the Accumulator data
type by using the Data Type Assistant. To use the
assistant, click the Show data type assistant
button![]() .
.
For more information on the data type assistant, see Specify Data Types Using Data Type Assistant (Simulink).
For a diagrammatic representation on how to use the accumulator data type in this block, see Fixed-Point Data Types.
Output — Data type of output
Inherit: Same as
accumulator (default) | Inherit: Same as input | Inherit: Same as product output | fixdt([],16,0)
Output specifies the data type of the output of the Convolution block.
Inherit: Same as accumulator— The block specifies the output data type to be the same as the accumulator data type.Inherit: Same as first input— The block specifies the output data type to be the same as the first input data type.Inherit: Same as product output— The block specifies the output data type to be the same as the product output data type.fixdt([],16,0)— The block specifies an autosigned, binary-point, scaled, fixed-point data type with a word length of 16 bits and a fraction length of 0.
Alternatively, you can set the Output data type
by using the Data Type Assistant. To use the
assistant, click the Show data type assistant
button![]() .
.
For more information, see Control Data Types of Signals (Simulink).
For more information on the output data type, see Fixed-Point Data Types.
Output Minimum — Minimum value that block can output
[]
(default) | scalar
Specify the minimum value the block can output. Simulink uses this minimum value to perform:
Simulation range checking. See Specify Signal Ranges (Simulink).
Automatic scaling of fixed-point data types.
Output Maximum — Maximum value that block can output
[]
(default) | scalar
Specify the maximum value the block can output. Simulink uses this maximum value to perform:
Simulation range checking. See Specify Signal Ranges (Simulink).
Automatic scaling of fixed-point data types.
Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types
off (default) | on
Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
Selecting the Appropriate Convolution Block
| Question | Answer | Recommended Block(s) |
|---|---|---|
How many convolutions do you intend to perform? | Many convolutions, one at each time step |
|
One convolution over the life of the simulation |
| |
How long are your input sequences? | Both sequences have a finite length |
|
One sequence has an infinite (not predetermined) length |
| |
How many of the inputs are scalar streams? | None |
|
One or both |
|
Convolving Two N-D Arrays
The block always computes the convolution of two N-D input arrays along the first dimension. When both inputs are N-D arrays, the size of their first dimension can differ, but the size of all other dimensions must be equal. For example, when u is an Mu-by-N-by-P array and v is an Mv-by-N-by-P array, the output is an (Mu+Mv–1)-by-N-by-P array.
When u is a Mu-by-N matrix and v is an Mv-by-N matrix, the output y is a (Mu+Mv–1)-by-N matrix whose jth column has these elements
Inputs u and v are zero when indexed outside their valid ranges. When both inputs are real, the output is real. When one or both inputs are complex, the output is complex.
Convolving a Column Vector with an N-D Array
When one input is a column vector and the other is an N-D array, the block independently convolves the vector with the first dimension of the N-D input array. For example, when u is a Mu-by-1 column vector and v is an Mv-by-N matrix, the output is an (Mu+Mv–1)-by-N matrix whose jth column has these elements:
Convolving Two Column Vectors
The Convolution block also accepts two column vector inputs. When u and v are column vectors with lengths Mu and Mv, the Convolution block performs the vector convolution with lengths Mu and Mv such that:
The output is a (Mu+Mv–1)-by-1 column vector.
Fixed-Point Data Types
This diagram shows the data types used within the Convolution block for fixed-point signals (time domain only).
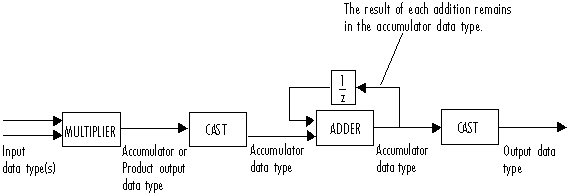
You can set the product output, accumulator, and output data types in the block dialog as discussed in Parameters.
The output of the multiplier is in the product output data type when the input is real. When the input is complex, the result of the multiplication is in the accumulator data type. For details on how the multiplication operation is performed, see Multiplication Data Types.
Note
When one or both of the inputs are signed fixed-point signals, all internal block data types are signed fixed point. The internal block data types are unsigned fixed point only when both inputs are unsigned fixed-point signals.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
