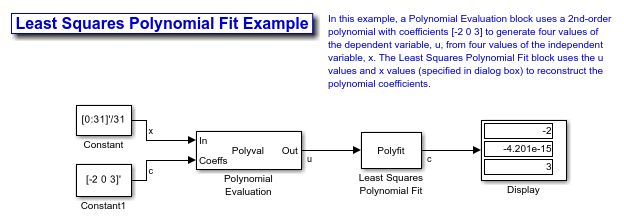
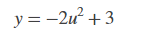Least Squares Polynomial Fit
Compute polynomial coefficients that best fit input data in least-squares sense
Libraries:
DSP System Toolbox /
Math Functions /
Polynomial Functions
Description
The Least Squares Polynomial Fit block computes the coefficients of the nth order polynomial that best fits the input data in the least-squares sense, where n is the value you specify in the Polynomial order parameter. The block computes a distinct set of n+1 coefficients for each column of the M-by-N input u.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Algorithms
For a given input column, the block computes the set of coefficients, c1, c2, ..., cn+1, that minimizes the quantity , where ui is the ith element in the input column and is given by:
The values of the independent variable, x1, x2, ..., xM are specified as a length-M vector by the Control points parameter. The same M control points are used for all N polynomial fits, and can be equally or unequally spaced.
The equivalent MATLAB® code is shown below.
c = polyfit(x,u,n)
Extended Capabilities
Version History
Introduced before R2006a