fitSmoothingSpline
Fit smoothing spline to bond market data
Syntax
Description
CurveObj = IRFunctionCurve.fitSmoothingSpline(Type,Settle,Instruments,Lambdafun)
Note
You must have a license for Curve Fitting Toolbox™ software to use the fitSmoothingSpline
method.
CurveObj = IRFunctionCurve.fitSmoothingSpline(___,Name,Value)
Examples
Input Arguments
Output Arguments
Algorithms
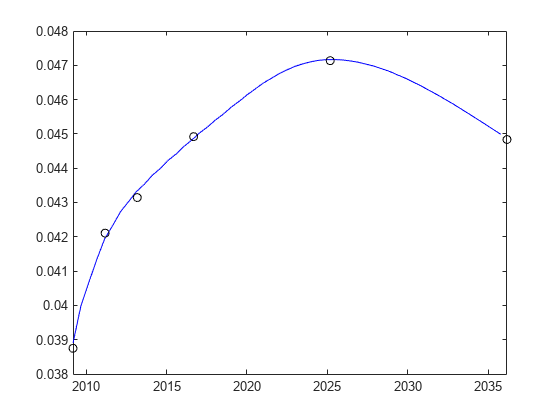
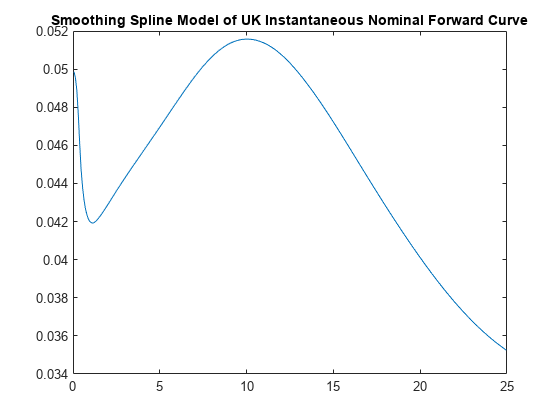
The term structure can be modeled with a spline — specifically, one way to model the term structure is by representing the forward curve with a cubic spline. To ensure that the spline is sufficiently smooth, a penalty is imposed relating to the curvature (second derivative) of the spline:
![]()
where the first term is the difference between the observed price P and the predicted price, , (weighted by the bond's duration, D) summed over all bonds in our data set and the second term is the penalty term (where λ is a penalty function and f is the spline).
See [3], [4], [5] below.
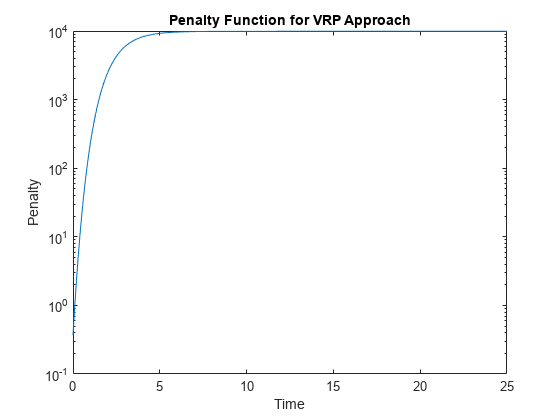
There have been different proposals for the specification of the penalty function λ. One approach, advocated by [4], and currently used by the UK Debt Management Office, is a penalty function of the following form:
![]()
References
[1] Nelson, C.R., Siegel, A.F. “Parsimonious modelling of yield curves.” Journal of Business. Vol. 60, 1987, pp 473–89.
[2] Svensson, L.E.O. “Estimating and interpreting forward interest rates: Sweden 1992-4.” International Monetary Fund, IMF Working Paper, 1994/114.
[3] Fisher, M., Nychka, D., Zervos, D. “Fitting the term structure of interest rates with smoothing splines.” Board of Governors of the Federal Reserve System, Federal Reserve Board Working Paper 1995-1.
[4] Anderson, N., Sleath, J. “New estimates of the UK real and nominal yield curves.” Bank of England Quarterly Bulletin, November, 1999, pp 384–92.
[5] Waggoner, D. “Spline Methods for Extracting Interest Rate Curves from Coupon Bond Prices.” Federal Reserve Board Working Paper 1997–10.
[6] “Zero-coupon yield curves: technical documentation.” BIS Papers No. 25, October 2005.
[7] Bolder, D.J., Gusba, S. “Exponentials, Polynomials, and Fourier Series: More Yield Curve Modelling at the Bank of Canada.” Working Papers 2002–29, Bank of Canada.
[8] Bolder, D.J., Streliski, D. “Yield Curve Modelling at the Bank of Canada.” Technical Reports 84, 1999, Bank of Canada.
Version History
Introduced in R2008b