step
Step response of dynamic system
Syntax
Description
step computes the step response to a step change in input
value from U to U + dU after td time units.
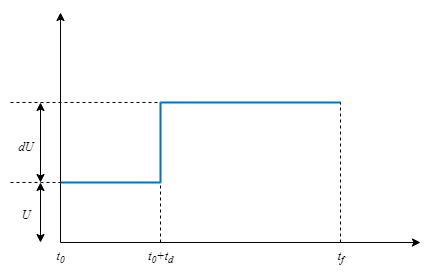
Here,
t0 is the start time.
td is the step delay.
tf is the final time.
U is the baseline input value.
dU is the step amplitude.
By default, the function applies step for t0 =
0, U = 0, dU = 1, and
td = 0. But, you can configure these values using
RespConfig. You can also specify the initial state
x(t0). When you don't,
step assumes the system is initially at rest with input level
U.
[
computes the step response from y,tOut] = step(sys,[t0,tFinal])t0 to tFinal. For
response configurations with a step delay td, the function applies the
step at time t = t0 + td. (since R2023b)
[
specifies additional options for computing the step response, such as the step amplitude
(dU) or input offset (U). Use y,tOut] = step(sys,___,config)RespConfig to create the option set config. You
can use config with any of the previous input-argument and
output-argument combinations.
Examples
Input Arguments
Output Arguments
Tips
Algorithms
To obtain samples of continuous-time models without internal delays,
step converts such models to state-space models and discretizes them
using a zero-order hold on the inputs. step chooses the sampling time for
this discretization automatically based on the system dynamics, except when you supply the
input time vector t in the form t = T0:dt:Tf. In that
case, step uses dt as the sampling time. The resulting
simulation time steps tOut are equisampled with spacing
dt.
For systems with internal delays, Control System Toolbox™ software uses variable step solvers. As a result, the time steps
tOut are not equisampled.
References
[1] L.F. Shampine and P. Gahinet, "Delay-differential-algebraic equations in control theory," Applied Numerical Mathematics, Vol. 56, Issues 3–4, pp. 574–588.
Version History
Introduced before R2006aSee Also
Functions
impulse|RespConfig|initial(Control System Toolbox) |lsim|stepplot
Apps
- Linear System Analyzer (Control System Toolbox)