graycomatrix
Create gray-level co-occurrence matrix from image
Description
glcm = graycomatrix(I)I. Another
name for a gray-level co-occurrence matrix is a gray-level spatial
dependence matrix.
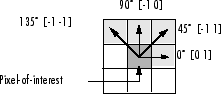
graycomatrix creates the GLCM by calculating how often a pixel with
gray-level (grayscale intensity) value i occurs horizontally
adjacent to a pixel with the value j. (You can specify other
pixel spatial relationships using the Offsets name-value
argument.) Each element (i,j) in glcm
specifies the number of times that the pixel with value i
occurred horizontally adjacent to a pixel with value j.
glcm = graycomatrix(I,Name=Value)
Examples
Input Arguments
Output Arguments
Algorithms
graycomatrix calculates the GLCM from a scaled version of the image. By
default, if I is a binary image, graycomatrix
scales the image to two gray-levels. If I is an intensity image,
graycomatrix scales the image to eight gray-levels. You can
specify the number of gray levels graycomatrix uses to scale the
image by using the NumLevels name-value argument, and the way that
graycomatrix scales the values using the
GrayLimits name-value argument.
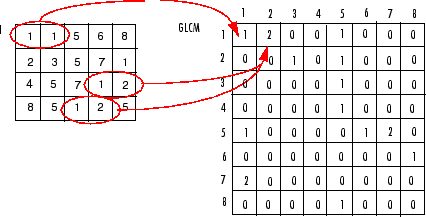
The following figure shows how graycomatrix calculates several values in
the GLCM of the 4-by-5 image I. Element (1,1) in the GLCM contains
the value 1 because there is only one instance in the image where
two, horizontally adjacent pixels have the values 1 and
1. Element (1,2) in the GLCM contains the
value 2 because there are two instances in the image where two,
horizontally adjacent pixels have the values 1 and
2. graycomatrix continues this processing to
fill in all the values in the GLCM.
graycomatrix ignores pixel pairs if either of the pixels contains a
NaN, replaces positive Infs with the value
NumLevels, and replaces negative Infs with
the value 1. graycomatrix ignores border pixels,
if the corresponding neighbor pixel falls outside the image boundaries.
The GLCM created when Symmetric is set to true is
symmetric across its diagonal, and is equivalent to the GLCM described by Haralick
(1973). The GLCM produced by the following syntax, with Symmetric
set to true
graycomatrix(I,Offset=[0 1],Symmetric=true)
is equivalent to the sum of the two GLCMs produced by the following statements where
Symmetric is set to false.
graycomatrix(I,Offset=[0 1],Symmetric=false) graycomatrix(I,Offset=[0 -1],Symmetric=false)
References
[1] Haralick, R.M., K. Shanmugan, and I. Dinstein, "Textural Features for Image Classification", IEEE Transactions on Systems, Man, and Cybernetics, Vol. SMC-3, 1973, pp. 610-621.
[2] Haralick, R.M., and L.G. Shapiro. Computer and Robot Vision: Vol. 1, Addison-Wesley, 1992, p. 459.
Version History
Introduced before R2006a