mpcmoveopt
Option set for mpcmove function
Description
To specify options for the mpcmove, mpcmoveAdaptive, and mpcmoveMultiple functions, use an mpcmoveopt
object.
Using this object, you can specify run-time values for a subset of controller properties,
such as tuning weights and constraints. If you do not specify a value for one of the
mpcmoveopt properties, the value of the corresponding controller option
is used instead.
Creation
Syntax
Description
options = mpcmoveoptmpcmove function. To modify the property values,
use dot notation.
Properties
OutputWeights — Output variable tuning weights
[] (default) | vector | array
Output variable tuning weights that replace the
Weights.OutputVariables property of the controller at run time,
specified as a vector or array of nonnegative values.
To use the same weights across the prediction horizon, specify a row vector of length Ny, where Ny is the number of output variables.
To vary the tuning weights over the prediction horizon from time k+1 to time k+p, specify an array with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the output variable tuning weights for one prediction horizon step. If you specify fewer than p rows, the weights in the final row are used for the remaining steps of the prediction horizon.
The format of OutputWeights must match the format of the
Weights.OutputVariables property of the controller object. For
example, you cannot specify constant weights across the prediction horizon in the
controller object, and then specify time-varying weights using
mpcmoveopt.
MVWeights — Manipulated variable tuning weights
[] (default) | vector | array
Manipulated variable tuning weights that replace the
Weights.ManipulatedVariables property of the controller at run
time, specified as a vector or array of nonnegative values.
To use the same weights across the prediction horizon, specify a row vector of length Nmv, where Nmv is the number of manipulated variables.
To vary the tuning weights over the prediction horizon from time k to time k+p-1, specify an array with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the manipulated variable tuning weights for one prediction horizon step. If you specify fewer than p rows, the weights in the final row are used for the remaining steps of the prediction horizon.
The format of MVWeights must match the format of the
Weights.ManipulatedVariables property of the controller object. For
example, you cannot specify constant weights across the prediction horizon in the
controller object, and then specify time-varying weights using
mpcmoveopt.
MVRateWeights — Manipulated variable rate tuning weights
[] (default) | vector | array
Manipulated variable rate tuning weights that replace the
Weights.ManipulatedVariablesRate property of the controller at run
time, specified as a vector or array of nonnegative values.
To use the same weights across the prediction horizon, specify a row vector of length Nmv, where Nmv is the number of manipulated variables.
To vary the tuning weights over the prediction horizon from time k to time k+p-1, specify an array with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the manipulated variable rate tuning weights for one prediction horizon step. If you specify fewer than p rows, the weights in the final row are used for the remaining steps of the prediction horizon.
The format of MVRateWeights must match the format of the
Weights.ManipulatedVariablesRate property of the controller object.
For example, you cannot specify constant weights across the prediction horizon in the
controller object, and then specify time-varying weights using
mpcmoveopt.
ECRWeight — Slack variable tuning weight
[] (default) | positive scalar
Slack variable tuning weight that replaces the Weights.ECR
property of the controller at run time, specified as a positive scalar.
OutputMin — Output variable lower bounds
[] (default) | row vector | matrix
Output variable lower bounds, specified as a row vector of length Ny or as a matrix with Ny columns, where Ny is the number of output variables.
If you did not specify the OutputVariables(i).Min property of the
mpc object, then specifying OutputMin results in an error
when you execute mpcmove.
To change the bounds over the prediction horizon from time k+1 to time k+p, specify a matrix with Ny columns and up to p rows. Here, Ny is the number of plant outputs, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row are used for the remaining steps of the prediction horizon.
OutputMin(:,i) replaces the
OutputVariables(i).Min property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar OutputVariables(i).Min in the mpc
object (a constant bound for the ith plant output to be applied to
all prediction steps)
OutputMin Dimension | Replacement Behavior |
|---|---|
Scalar OutputMin (single output, constant
bound) | OutputMin replaces the constant bound defined in
OutputVariables(i).Min. |
Column vector OutputMin (single output, time-varying
bound) | OutputMin replaces the constant bound defined in
OutputVariables(i).Min with a time-varying bound. |
Row vector OutputMin (multiple outputs, constant
bounds) | OutputMin(i) replaces the constant bound defined in
OutputVariables(i).Min. |
Matrix OutputMin (multiple outputs, time-varying
bounds) | OutputMin(:,i) replaces the constant bound defined in
OutputVariables(i).Min with a time-varying bound. |
Vector OutputVariables(i).Min in the mpc
object (a time-varying bound for the ith plant output with
different values at different prediction steps)
OutputMin Dimension | Replacement Behavior |
|---|---|
Scalar OutputMin (single output, constant
bound) | OutputMin replaces the first finite entry
in OutputVariables.Min and the remaining entries in
OutputVariables.Min shift up or down with the same amount
of displacement to retain the profile defined by the original
OutputVariables.Min vector. |
Column vector OutputMin (single output, time-varying
bound) | OutputMin replaces the time-varying bound defined in
OutputVariables(i).Min, and the original bound profile is
discarded. |
Row vector OutputMin (multiple outputs, constant
bounds) | OutputMin(i) replaces the first finite entry
in OutputVariables(i).Min and the remaining entries in
OutputVariables(i).Min shift up or down with the same
amount of displacement to retain the profile defined by the original
OutputVariables(i).Min vector. |
Matrix OutputMin (multiple outputs, time-varying
bounds). | OutputMin(:,i) replaces the time-varying bound defined
in OutputVariables(i).Min, and the original bound profile is
discarded. |
OutputMax — Output variable upper bounds
[] (default) | row vector | matrix
Output variable upper bounds, specified as a row vector of length Ny or as a matrix with Ny columns, where Ny is the number of output variables.
If you did not specify the OutputVariables(i).Max property of the
mpc object, then specifying OutputMax results in an error
when you execute mpcmove.
To change the bounds over the prediction horizon from time k+1 to time k+p, specify a matrix with Ny columns and up to p rows. Here, Ny is the number of plant outputs, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row are used for the remaining steps of the prediction horizon.
OutputMax(:,i) replaces the
OutputVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar OutputVariables(i).Max in the mpc
object (a constant bound for the ith plant output to be applied to
all prediction steps)
OutputMax Dimension | Replacement Behavior |
|---|---|
Scalar |
|
Column vector |
|
Row vector |
|
Matrix |
|
Vector OutputVariables(i).Max in the mpc
object (a time-varying bound for the ith plant output with
different values at different prediction steps)
OutputMax Dimension | Replacement Behavior |
|---|---|
Scalar OutputMax (single output, constant
bound) | OutputMax replaces the first finite entry
in OutputVariables.Max and the remaining entries in
OutputVariables.Max shift up or down with the same amount
of displacement to retain the profile defined by the original
OutputVariables.Max vector. |
Column vector OutputMax (single output, time-varying
bound) | OutputMax replaces the time-varying bound defined in
OutputVariables(i).Max, and the original bound profile is
discarded. |
Row vector OutputMax (multiple outputs, constant
bounds) | OutputMax(i) replaces the first finite entry
in OutputVariables(i).Max and the remaining entries in
OutputVariables(i).Max shift up or down with the same
amount of displacement to retain the profile defined by the original
OutputVariables(i).Max vector. |
Matrix OutputMax (multiple outputs, time-varying
bounds). | OutputMax(:,i) replaces the time-varying bound defined
in OutputVariables(i).Max, and the original bound profile is
discarded. |
MVMin — Manipulated variable lower bounds
[] (default) | row vector | matrix
Manipulated variable lower bounds, specified as a row vector of length Nmv or as a matrix with Nmv columns, where Nmv is the number of output variables.
If you did not specify the ManipulatedVariables(i).Min property
of the mpc object, then specifying
MVMin results in an error when you execute mpcmove.
To change the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with Nmv columns and up to p rows. Here, Nmv is the number of manipulated variables, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row are used for the remaining steps of the prediction horizon.
MVMin(:,i) replaces the
ManipulatedVariables(i).Min property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar ManipulatedVariables(i).Min in the mpc
object (a constant bound for the ith manipulated variable to be
applied to all prediction steps)
MVMin Dimension | Replacement Behavior |
|---|---|
Scalar MVMin (single output, constant bound) | MVMin replaces the constant bound defined in
ManipulatedVariables(i).Min |
Column vector MVMin (single output, time-varying
bound) | MVMin replaces the constant bound defined in
ManipulatedVariables(i).Min with a time-varying
bound. |
Row vector MVMin (multiple outputs, constant
bounds) | MVMin(i) replaces the constant bound defined in
ManipulatedVariables(i).Min |
Matrix MVMin (multiple outputs, time-varying
bounds) | MVMin(:,i) replaces the constant bound defined in
ManipulatedVariables(i).Min with a time-varying
bound. |
Vector ManipulatedVariables(i).Min in the mpc
object (a time-varying bound for the ith manipulated variable with
different values at different prediction steps)
MVMin Dimension | Replacement Behavior |
|---|---|
Scalar MVMin (single output, constant bound) | MVMin replaces the first finite entry
in ManipulatedVariables.Min and the remaining entries in
ManipulatedVariables.Min shift up or down with the same
amount of displacement to retain the profile defined by the original
ManipulatedVariables.Min vector. |
Column vector MVMin (single output, time-varying
bound) | MVMin replaces the time-varying bound defined in
ManipulatedVariables(i).Min, and the original bound profile
is discarded. |
Row vector MVMin (multiple outputs, constant
bounds) | MVMin(i) replaces the first finite entry
in ManipulatedVariables(i).Min and the remaining entries in
ManipulatedVariables(i).Min shift up or down with the same
amount of displacement to retain the profile defined by the original
ManipulatedVariables(i).Min vector. |
Matrix MVMin (multiple outputs, time-varying
bounds). | MVMin(:,i) replaces the time-varying bound defined in
ManipulatedVariables(i).Min, and the original bound profile
is discarded. |
MVMax — Manipulated variable upper bounds
[] (default) | row vector | matrix
Manipulated variable upper bounds, specified as a row vector of length Nmv or as a matrix with Nmv columns, where Nmv is the number of output variables.
If you did not specify the ManipulatedVariables(i).Max property
of the mpc object, then specifying
MVMax results in an error when you execute mpcmove.
To change the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with Nmv columns and up to p rows. Here, Nmv is the number of manipulated variables, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row are used for the remaining steps of the prediction horizon.
MVMax(:,i) replaces the
ManipulatedVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar ManipulatedVariables(i).Max in the mpc
object (a constant bound for the ith manipulated variable to be
applied to all prediction steps)
MVMax Dimension | Replacement Behavior |
|---|---|
Scalar MVMax (single output, constant bound) | MVMax replaces the constant bound defined in
ManipulatedVariables(i).Max. |
Column vector MVMax (single output, time-varying
bound) | MVMax replaces the constant bound defined in
ManipulatedVariables(i).Max with a time-varying
bound. |
Row vector MVMax (multiple outputs, constant
bounds) | MVMax(i) replaces the constant bound defined in
ManipulatedVariables(i).Max. |
Matrix MVMax (multiple outputs, time-varying
bounds) | MVMax(:,i) replaces the constant bound defined in
ManipulatedVariables(i).Max with a time-varying
bound. |
Vector ManipulatedVariables(i).Max in the mpc
object (a time-varying bound for the ith manipulated variable with
different values at different prediction steps)
MVMax Dimension | Replacement Behavior |
|---|---|
Scalar MVMax (single output, constant bound) | MVMax replaces the first finite entry
in ManipulatedVariables.Max and the remaining entries in
ManipulatedVariables.Max shift up or down with the same
amount of displacement to retain the profile defined by the original
ManipulatedVariables.Max vector. |
Column vector MVMax (single output, time-varying
bound) | MVMax replaces the time-varying bound defined in
ManipulatedVariables(i).Max, and the original bound profile
is discarded. |
Row vector MVMax (multiple outputs, constant
bounds) | MVMax(i) replaces the first finite entry
in ManipulatedVariables(i).Max and the remaining entries in
ManipulatedVariables(i).Max shift up or down with the same
amount of displacement to retain the profile defined by the original
ManipulatedVariables(i).Max vector. |
Matrix MVMax (multiple outputs, time-varying
bounds). | MVMax(:,i) replaces the time-varying bound defined in
ManipulatedVariables(i).Max, and the original bound profile
is discarded. |
CustomConstraint — Custom mixed input/output constraints
[] (default) | structure
Custom mixed input/output constraints, specified as a structure with the following
fields. These constraints replace the mixed input/output constraints previously set
using setconstraint.
E — Manipulated variable constraint constant
array of zeros (default) | Nc-by-Nmv
array
Manipulated variable constraint constant, specified as an Nc-by-Nmv array, where Nc is the number of constraints, and Nmv is the number of manipulated variables.
F — Controlled output constraint constant
array of zeros (default) | Nc-by-Ny
array
Controlled output constraint constant, specified as an Nc-by-Ny array, where Ny is the number of controlled outputs (measured and unmeasured).
G — Mixed input/output constraint constant
column vector of zeros (default) | column vector of length Nc
Mixed input/output constraint constant, specified as a column vector of length Nc.
S — Measured disturbance constraint constant
array of zeros (default) | Nc-by-Nmd
array
Measured disturbance constraint constant, specified as an Nc-by-Nmd array, where Nmd is the number of measured disturbances.
OnlyComputeCost — Option to return only the value of the cost function in the solution details structure
0 (default) | 1
Option to return only the value of the cost function in the info solution details output
structure returned by mpcmove. Specify it as one of the
following:
0—mpcmovereturns all the detailed solution information in its second output argument.1—mpcmovereturns only the predicted value of the cost function. This saves some computational effort as the predicted optimal plant state and output sequences do not need to be calculated. Note that ifmpcmoveis not called with a second output argument these sequences are not calculated either.
MVused — Manipulated variable values used in the plant during the previous control interval
[] (default) | row vector
Manipulated variable values used in the plant during the previous control interval,
specified as a row vector of length Nmv, where
Nmv is the number of manipulated
variables. If you do not specify MVused, the
mpvmove uses the LastMove property of its
current controller state input argument, x.
MVTarget — Manipulated variable targets
[] (default) | row vector
Manipulated variable targets, specified as a row vector of length
Nmv, where
Nmv is the number of manipulated
variables. MVTarget(i) replaces the
ManipulatedVariables(i).Target property of the controller at run
time.
PredictionHorizon — Prediction horizon
[] (default) | positive integer
Prediction horizon, which replaces the PredictionHorizon property
of the controller at run time, specified as a positive integer. If you specify
PredictionHorizon, you must also specify
ControlHorizon.
Specifying PredictionHorizon changes the:
Number of rows in the optimal sequences returned by the
mpcmoveandmpcmoveAdaptivefunctionsMaximum dimensions of the
PlantandNominalinput arguments ofmpcmoveAdaptive
This parameter is ignored by the mpcmoveMultiple
function.
ControlHorizon — Control horizon
[] (default) | positive integer | vector of positive integers
Control horizon, which replaces the ControlHorizon property of
the controller at run time, specified as one of the following:
Positive integer, m, between
1and p, inclusive, where p is equal toPredictionHorizon. In this case, the controller computes m free control moves occurring at times k through k+m-1, and holds the controller output constant for the remaining prediction horizon steps from k+m through k+p-1. Here, k is the current control interval. For optimal trajectory planning set m equal to p.Vector of positive integers, [m1, m2, …], where the sum of the integers equals the prediction horizon, p. In this case, the controller computes M blocks of free moves, where M is the length of the
ControlHorizonvector. The first free move applies to times k through k+m1-1, the second free move applies from time k+m1 through k+m1+m2-1, and so on. Using block moves can improve the robustness of your controller compared to the default case.
If you specify ControlHorizon, you must also specify
PredictionHorizon.
This parameter is ignored by the mpcmoveMultiple
function.
Object Functions
mpcmove | Compute optimal control action and update controller states |
mpcmoveAdaptive | Compute optimal control with prediction model updating |
mpcmoveMultiple | Compute gain-scheduling MPC control action at a single time instant |
Examples
Simulation with Varying Controller Property
Vary a manipulated variable upper bound during a simulation.
Define the plant, which includes a 4-second input delay. Convert to a delay-free, discrete, state-space model using a 2-second control interval. Create the corresponding default controller, and specify MV bounds at +/-2.
Ts = 2; Plant = absorbDelay(c2d(ss(tf(0.8,[5 1],InputDelay=4)),Ts)); mpcobj = mpc(Plant,Ts);
-->"PredictionHorizon" is empty. Assuming default 10. -->"ControlHorizon" is empty. Assuming default 2. -->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
mpcobj.MV(1).Min = -2; mpcobj.MV(1).Max = 2;
Create an empty mpcmoveopt object. During simulation, you can set properties of the object to specify controller parameters.
options = mpcmoveopt;
Pre-allocate storage and initialize the controller state.
v = []; t = [0:Ts:20]; N = length(t); y = zeros(N,1); u = zeros(N,1); x = mpcstate(mpcobj);
-->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output.
Use mpcmove to simulate the following:
Reference (setpoint) step change from initial condition r = 0 to r = 1 (servo response)
MV upper bound step decrease from 2 to 1, occurring at t = 10
r = 1; for i = 1:N y(i) = Plant.C*x.Plant; if t(i) >= 10 options.MVMax = 1; end [u(i),Info] = mpcmove(mpcobj,x,y(i),r,v,options); end
As the loop executes, the value of options.MVMax is reset to 1 for all iterations that occur after t = 10. Prior to that iteration, options.MVMax is empty. Therefore, the controller's value for MVMax is used, mpcobj.MV(1).Max = 2.
Plot the results of the simulation.
[Ts,us] = stairs(t,u); plot(Ts,us,'b-',t,y,'r-') legend('MV','OV') xlabel(sprintf('Time, %s',Plant.TimeUnit))
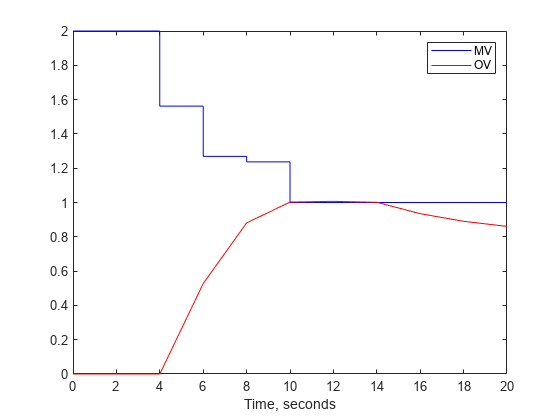
From the plot, you can observe that the original MV upper bound is active until t = 4. After the input delay of 4 seconds, the output variable (OV) moves smoothly to its new target of r = 1. reaching the target at t = 10. The new MV bound imposed at t = 10 becomes active immediately. This forces the OV below its target, after the input delay elapses.
Now assume that you want to impose an OV upper bound at a specified location relative to the OV target. Consider the following constraint design command:
mpcobj.OV(1).Max = [Inf,Inf,0.4,0.3,0.2];
This is a horizon-varying constraint. The known input delay makes it impossible for the controller to satisfy an OV constraint prior to the third prediction-horizon step. Therefore, a finite constraint during the first two steps would be poor practice. For illustrative purposes, the previous constraint also decreases from 0.4 at step 3 to 0.2 at step 5 and thereafter.
The following commands produce the same results shown in the previous plot. The OV constraint is never active because it is being varied in concert with the setpoint, r.
x = mpcstate(mpcobj);
-->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output.
OPTobj = mpcmoveopt; for i = 1:N y(i) = Plant.C*x.Plant; if t(i) >= 10 OPTobj.MVMax = 1; end OPTobj.OutputMax = r + 0.4; [u(i),Info] = mpcmove(mpcobj,x,y(i),r,v,OPTobj); end
The scalar value r + 0.4 replaces the first finite value in the mpcobj.OV(1).Max vector, and the remaining finite values adjust to maintain the original profile, that is, the numerical difference between these values is unchanged. r = 1 for the simulation, so the previous use of the mpcmoveopt object is equivalent to the command
mpcobj.OV(1).Max = [Inf, Inf, 1.4, 1.3, 1.2];
However, using the mpcmoveopt object involves much less computational overhead.
Tips
If a variable is unconstrained in the initial controller design, you cannot constrain it using
mpcmoveopt. The controller ignores any such specifications.You cannot remove a constraint from a variable that is constrained in the initial controller design. However, you can change it to a large (or small) value such that it is unlikely to become active.
Version History
Introduced in R2018b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)