initmesh
Create initial 2-D mesh
This page describes the legacy workflow. New features might not be compatible with the
legacy workflow. For the corresponding step in the recommended workflow, see generateMesh.
Description
Examples
Initial Mesh for L-shaped Membrane
Generate a triangular mesh of the L-shaped membrane.
[p,e,t] = initmesh("lshapeg");Plot the mesh.
pdemesh(p,e,t)

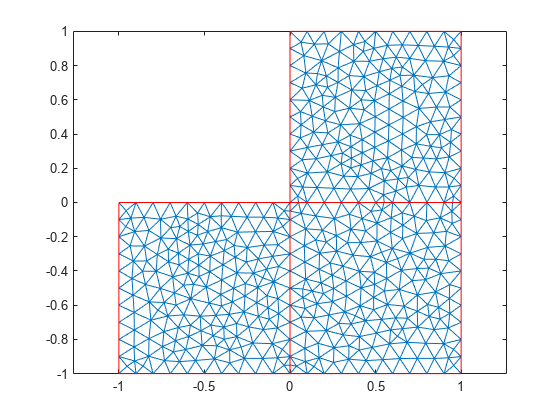
Maximum Mesh Edge Length
Generate a triangular mesh of the L-shaped membrane with the target maximum mesh edge length of 0.1.
[p,e,t] = initmesh("lshapeg","Hmax",0.1);
Plot the mesh.
pdemesh(p,e,t)
Input Arguments
g — Geometry description
decomposed geometry matrix | geometry function | handle to geometry function
Geometry description, specified as a decomposed geometry matrix, a geometry
function, or a handle to the geometry function. For details about a decomposed geometry
matrix, see decsg. For details about a geometry function,
see Parametrized Function for 2-D Geometry Creation.
A geometry function must return the same result for the same input arguments in every function call. Thus, it must not contain functions and expressions designed to return a variety of results, such as random number generators.
Data Types: double | char | string | function_handle
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: [p,e,t] = initmesh("lshapeg","Hmax",0.1);
Hmax — Target maximum mesh edge length
positive real number
Target maximum mesh edge length, specified as the comma-separated pair consisting
of "Hmax" and a positive real number.
Hmax is an approximate upper bound on the mesh edge lengths.
initmesh estimates the default value of Hmax
from overall dimensions of the geometry.
Small Hmax values let you create finer meshes, but mesh
generation can take a very long time in this case. You can interrupt mesh generation
by using Ctrl+C. Note that initmesh can take
additional time to respond to the interrupt.
Example: [p,e,t] = initmesh(g,"Hmax",0.25);
Data Types: double
Hgrad — Mesh growth rate
1.3 (default) | number strictly greater than 1 and less than 2
Mesh growth rate, specified as the comma-separated pair consisting of
"Hgrad" and a number strictly greater than 1 and less than
2.
Example: [p,e,t] = initmesh(g,"Hgrad",1.5);
Data Types: double
Box — Toggle to preserve bounding box
"off" (default) | "on"
Toggle to preserve bounding box, specified as the comma-separated pair consisting
of "Box" and "on" or "off".
By turning on "Box" you can get a good idea of how the mesh
generation algorithm works within the bounding box.
Example: [p,e,t] = initmesh(g,"Box","on");
Data Types: char | string
Init — Toggle to use edge triangulation
"off" (default) | "on"
Toggle to use edge triangulation, specified as the comma-separated pair consisting
of "Init" and "on" or "off".
By turning on Init you can see the initial triangulation of the
boundaries. For example, use these commands to determine the subdomain number
n of the point xy.
[p,e,t] = initmesh(g,"Hmax",Inf,"Init","on"); [uxy,tn,a2,a3] = tri2grid(p,t,zeros(size(p,2)),x,y); n = t(4,tn);
If the point is outside the geometry, tn is
NaN, and the command n = t(4,tn) results in a
failure.
Data Types: char | string
Jiggle — Toggle to call jigglemesh after creating the mesh
"mean" (default) | "minimum" | "on" | "off"
Toggle to call jigglemesh after creating the mesh, specified
as the comma-separated pair consisting of "Jiggle" and
"mean", "minimum""on", or
"off".
"mean"— calljigglemeshwith the argument"Opt"set to"mean"."minimum"— calljigglemeshwith the argument"Opt"set to"minimum"."on"— calljigglemeshwith the argument"Opt"set to"off"."off"— do not calljigglemesh.
Example: [p,e,t] =
initmesh(g,"Jiggle","minimum");
Data Types: char | string
JiggleIter — Maximum number of iterations for jigglemesh
10 (default) | positive integer
Maximum number of iterations for jigglemesh, specified as the
comma-separated pair consisting of "JiggleIter" and a positive
integer.
Example: [p,e,t] =
initmesh(g,"Jiggle","on","JiggleIter",50);
Data Types: double
MesherVersion — Algorithm for generating initial mesh
"preR2013a" (default) | "R2013a"
Algorithm for generating initial mesh, specified as the comma-separated pair
consisting of "MesherVersion" and either
"R2013a" or "preR2013a". The
"R2013a" algorithm runs faster, and can triangulate more
geometries than the "preR2013a" algorithm. Both algorithms use
Delaunay triangulation.
Data Types: char | string
Output Arguments
p — Mesh points
2-by-Np matrix
Mesh points, returned as a 2-by-Np matrix. Np
is the number of points (nodes) in the mesh. Column k of
p consists of the x-coordinate of point
k in p(1,k) and the
y-coordinate of point k in
p(2,k). For details, see Mesh Data as [p,e,t] Triples.
e — Mesh edges
7-by-Ne matrix
Mesh edges, returned as a 7-by-Ne matrix, where
Ne is the number of boundary edges in the mesh. An edge is a pair
of points in p containing a boundary between subdomains, or
containing an outer boundary. For details, see Mesh Data as [p,e,t] Triples.
t — Mesh elements
4-by-Nt matrix
Mesh elements, returned as a 4-by-Nt matrix.
Nt is the number of triangles in the mesh.
The t(i,k), with i ranging from 1 through
end - 1, contain indices to the corner points of element
k. For details, see Mesh Data as [p,e,t] Triples. The last row,
t(end,k), contains the subdomain number of the element.
References
[1] George, P. L. Automatic Mesh Generation — Application to Finite Element Methods. Wiley, 1991.
Version History
Introduced before R2006aR2013a: Performance and robustness enhancements in meshing algorithm
initmesh provides an enhancement option for increased meshing speed
and robustness. Choose the enhanced algorithm by setting the
MesherVersion name-value pair to 'R2013a'. The
default MesherVersion value of 'preR2013a' gives the
same mesh as previous toolbox versions.
The enhancement is available inpdeModeler from the Mesh
> Parameters > Mesher version menu.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)