Least Pth-Norm Optimal FIR Filter Design
This example shows how to design least Pth-norm FIR filters with the firlpnorm function. This function uses a least-Pth unconstrained optimization algorithm to design FIR filters with arbitrary magnitude response.
FIRLPNORM Syntax
The syntax for firlpnorm is similar to that of iirlpnorm (see the Least Pth-Norm Optimal IIR Filter Design example for details) except that the denominator order is not specified.
The function designs optimal FIR filters in the least-Pth sense. However the filter is not constrained to have linear-phase, that is, the impulse response has no special symmetry properties.
However, the linear-phase constraint also results in filters with larger order than the more general nonlinear-phase designs. Note that in some hardware implementations, one can reduce the number of multipliers in half when implementing linear-phase filters because of the symmetry in the coefficients. For example, consider the following firlpnorm design
N = 30; F = [0 0.3 0.45 1]; E = F; A = [1 1 0 0]; W = [1 1 10 10]; b = firlpnorm(N,F,E,A,W); hFiltAnalyzer = filterAnalyzer(b);

If we zoom in, we can see that the filter has a passband peak ripple of about 0.008 and a stopband peak ripple of about 0.000832. A firpm or firgr design with comparable specs will require a 37th order filter. This is especially significant considering that firgr will provide the lowest order linear-phase FIR filter that meets the specifications.
dev = [0.008 0.000832]; bgr = firgr("minorder",F,A,dev); orderfirgr = length(b)-1; fprintf("Order: %d\n",orderfirgr);
Order: 30
hFiltAnalyzer.addFilters(bgr); hFiltAnalyzer.setLegendStrings(["FIRLPNORM design" "FIRGR design"]);
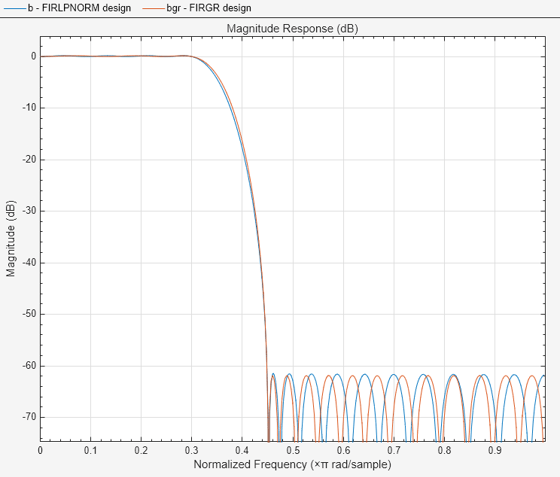
Another way to look at this is by using the firceqrip function which also designs linear-phase equiripple filters, but whose specifications are given in a different way to firgr (see the constrained equiripple FIR filter design example for details). If we want a linear-phase filter of 30th order that meets the passband and stopband ripple that the design from firlpnorm achieves we need to live with a larger transition width.
bceq = firceqrip(30,(F(2)+F(3))/2,dev); deleteFilters(hFiltAnalyzer, FilterNames="bgr"); addFilters(hFiltAnalyzer, bceq); setLegendStrings(hFiltAnalyzer,["FIRLPNORM design","FIRCEQRIP design"]);

Minimum-Phase Designs
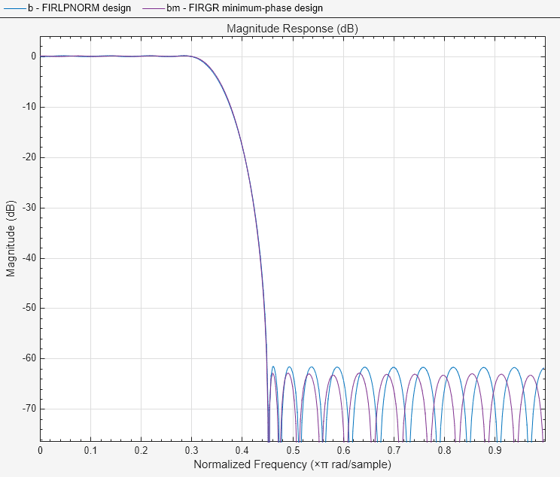
Of course it is also possible to design nonlinear-phase filters with firgr by specifying the minphase option. Doing so allows us to obtain an FIR filter of lower order than in the linear-phase case and still meet the required specs. However, even in this case, the result is a non-optimal nonlinear-phase filter because the filter order is larger than the minimum required for a nonlinear-phase equiripple filter to meet the specs as is evident from the following example.
bm = firgr("minorder",F,A,dev,"minphase"); orderfirgrmin = length(bm)-1; fprintf("Order: %d\n",orderfirgrmin);
Order: 32
deleteFilters(hFiltAnalyzer, FilterNames="bceq"); addFilters(hFiltAnalyzer, bm); setLegendStrings(hFiltAnalyzer,["FIRLPNORM design" "FIRGR minimum-phase design"]);
Minimum-Phase Designs with FIRLPNORM
firlpnorm does allow for the option to constrain the zeros to lie on or inside the unit circle, resulting in a minimum-phase design. The constraint, however, results in larger passband ripple and less stopband attenuation than the unconstrained design.
bmlp = firlpnorm(30,F,E,A,W,"minphase"); deleteFilters(hFiltAnalyzer, FilterNames="bm"); addFilters(hFiltAnalyzer, bmlp); setLegendStrings(hFiltAnalyzer,["FIRLPNORM design" "FIRLPNORM minimum-phase design"]);
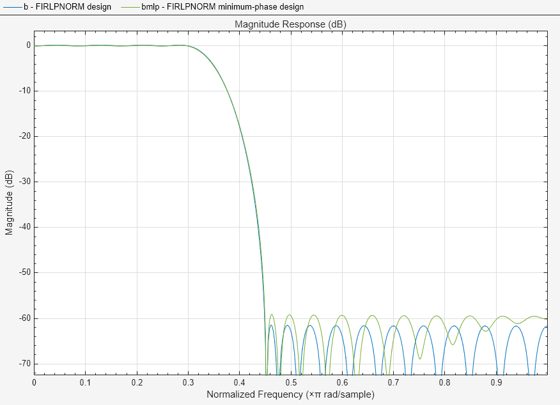
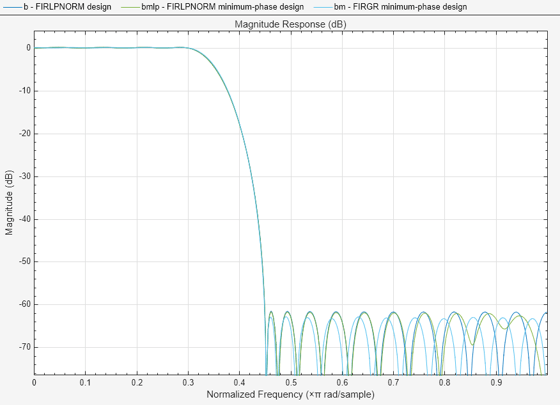
If we increase the order to that of the minimum-phase filter designed with firgr we can see that we meet the specs met by both the 30th order firlpnorm (nonminimum-phase) design and the 32nd order firgr minimum-phase design.
bmlp = firlpnorm(orderfirgrmin,F,E,A,W,"minphase"); replaceFilters(hFiltAnalyzer, bmlp,FilterNames="bmlp"); addFilters(hFiltAnalyzer,bm); setLegendStrings(hFiltAnalyzer,["FIRLPNORM design" "FIRLPNORM minimum-phase design" "FIRGR minimum-phase design"]);
Changing the Pth-Norm
Like iirlpnorm and iirlpnormc, firlpnorm allows for the specification of the Pth-norm used to optimize the filter. The Pth-norm is specified in the exact same way as in iirlpnorm, i.e. a two element vector with Pinit and Pfinal as its elements. Pinit specifies the initial Pth-norm used by the algorithm (this aids in the convergence) and Pfinal specifies the final Pth-norm with which the filter is optimized.
For example, a least-squares design for the above specs can be obtained as follows:
N = 40;
F = [0 0.4 0.45 1];
E = F;
A = [0 0 1 1];
W = [1 1 10 10];
P = [2 2];
bl2 = firlpnorm(N,F,E,A,W,P);
addDisplays(hFiltAnalyzer,1);
addFilters(hFiltAnalyzer, bl2);
setLegendStrings(hFiltAnalyzer, "FIRLPNORM design");
Comparing to FIRLS
In comparison, we design a linear-phase least-squares filter using firls. Once again, for the same filter order, the linear-phase constraint results in less stopband attenuation and a larger passband ripple.
W = [1 20]; bls = firls(N,F,A,W); addFilters(hFiltAnalyzer,bls); setLegendStrings(hFiltAnalyzer, ["FIRLPNORM design" "FIRLS design"]);

Other Norms
Equiripple designs are useful when one requires the smallest possible order to meet a set of design specifications. To meet the same specs with a least-squares design requires a higher order filter. However, the higher order does provide extra attenuation (less ripple) for a large portion of the stopband (passband). In fact least-squares design minimize the energy of the stopband. Compromises between equiripple design and least-squares design can be reached by using intermediate norms. For example we show the design of a filter with the same specs, but optimized for the following norms: 2, 4, 12, 256 (approx. infinity norm).
W = [1 1 10 10]; P4 = [2 4]; bl4 = firlpnorm(N,F,E,A,W,P4); P12 = [2 12]; bl12 = firlpnorm(N,F,E,A,W,P12); Pinf = [2 256]; blinf = firlpnorm(N,F,E,A,W,Pinf); addDisplays(hFiltAnalyzer,1); addFilters(hFiltAnalyzer,bl2,1,bl4,1,bl12,1,blinf,1); setLegendStrings(hFiltAnalyzer, ["P = 2" "P = 4" "P = 12" "P = 256"]);

In order to meet the minimum stopband attenuation of the equiripple (256-norm) case, it is necessary to increase the order of the other designs.