Creating and Editing Delaunay Triangulations
This example shows how to create, edit, and query Delaunay triangulations using the delaunayTriangulation class. The Delaunay triangulation is the most widely used triangulation in scientific computing. The properties associated with the triangulation provide a basis for solving a variety of geometric problems. Construction of constrained Delaunay triangulations is also shown, together with an applications covering medial axis computation and mesh morphing.
Example One: Create and Plot 2-D Delaunay Triangulation
This example shows you how to compute a 2-D Delaunay triangulation and then plot the triangulation together with the vertex and triangle labels.
rng default
x = rand(10,1);
y = rand(10,1);
dt = delaunayTriangulation(x,y)dt =
delaunayTriangulation with properties:
Points: [10×2 double]
ConnectivityList: [11×3 double]
Constraints: []
triplot(dt)
Display the vertex and triangle labels on the plot.
hold on vxlabels = arrayfun(@(n) {sprintf('P%d', n)}, (1:10)'); Hpl = text(x,y,vxlabels,'FontWeight','bold','HorizontalAlignment',... 'center','BackgroundColor','none'); ic = incenter(dt); numtri = size(dt,1); trilabels = arrayfun(@(x) {sprintf('T%d',x)}, (1:numtri)'); Htl = text(ic(:,1),ic(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off

Example Two: Create and Plot 3-D Delaunay Triangulation
This example shows you how to compute and plot a 3-D Delaunay triangulation.
rng default
X = rand(10,3);
dt = delaunayTriangulation(X)dt =
delaunayTriangulation with properties:
Points: [10×3 double]
ConnectivityList: [18×4 double]
Constraints: []
tetramesh(dt) view([10 20])

To display large tetrahedral meshes, use the convexHull method to compute the boundary triangulation and plot it using trisurf. For example:
triboundary = convexHull(dt); trisurf(triboundary, X(:,1), X(:,2), X(:,3),'FaceColor','cyan')
Example Three: Access Triangulation Data Structure
There are two ways to access the triangulation data structure. One way is via the Triangulation property, the other way is using indexing.
Create a 2-D Delaunay triangulation from 10 random points.
rng default
X = rand(10,2);
dt = delaunayTriangulation(X)dt =
delaunayTriangulation with properties:
Points: [10×2 double]
ConnectivityList: [11×3 double]
Constraints: []
One way to access the triangulation data structure is with the ConnectivityList property.
dt.ConnectivityList
ans = 11×3
2 8 5
7 6 1
3 7 8
8 7 5
3 8 2
6 7 3
7 4 5
5 9 2
2 9 10
5 4 9
7 1 4
⋮
Indexing is a shorthand way to query the triangulation. The syntax is dt(i,j), where j is the jth vertex of the ith triangle. Standard indexing rules apply.
Query the triangulation data structure with indexing.
dt(:,:)
ans = 11×3
2 8 5
7 6 1
3 7 8
8 7 5
3 8 2
6 7 3
7 4 5
5 9 2
2 9 10
5 4 9
7 1 4
⋮
The second triangle is:
dt(2,:)
ans = 1×3
7 6 1
The third vertex of the second triangle is:
dt(2,3)
ans = 1
The first three triangles are:
dt(1:3,:)
ans = 3×3
2 8 5
7 6 1
3 7 8
Example Four: Edit Delaunay Triangulation to Insert or Remove Points
This example shows you how to use index-based subscripting to insert or remove points. It is more efficient to edit a delaunayTriangulation to make minor modifications as opposed to recreating a new delaunayTriangulation from scratch, this is especially true if the data set is large.
Construct a Delaunay triangulation from 10 random points within a unit square.
rng default
x = rand(10,1);
y = rand(10,1);
dt = delaunayTriangulation(x,y)dt =
delaunayTriangulation with properties:
Points: [10×2 double]
ConnectivityList: [11×3 double]
Constraints: []
Insert 5 additional random points.
dt.Points(end+(1:5),:) = rand(5,2)
dt =
delaunayTriangulation with properties:
Points: [15×2 double]
ConnectivityList: [20×3 double]
Constraints: []
Replace the fifth point.
dt.Points(5,:) = [0 0]
dt =
delaunayTriangulation with properties:
Points: [15×2 double]
ConnectivityList: [20×3 double]
Constraints: []
Remove the fourth point.
dt.Points(4,:) = []
dt =
delaunayTriangulation with properties:
Points: [14×2 double]
ConnectivityList: [18×3 double]
Constraints: []
Example Five: Create Constrained Delaunay Triangulation
This example shows you how to create a constrained Delaunay triangulation and illustrates the effect of the constraints.
Create and plot a constrained Delaunay triangulation.
X = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5]; C = [1 2; 2 3; 3 4; 4 5; 5 6; 6 7; 7 8; 8 1]; dt = delaunayTriangulation(X,C); subplot(2,1,1) triplot(dt) axis([-1 17 -1 6]) xlabel('Constrained Delaunay triangulation','FontWeight','b')
Plot the constrained edges in red.
hold on plot(X(C'),X(C'+size(X,1)),'-r','LineWidth',2) hold off
Now delete the constraints and plot the unconstrained Delaunay triangulation.
dt.Constraints = []; subplot(2,1,2) triplot(dt) axis([-1 17 -1 6]) xlabel('Unconstrained Delaunay triangulation','FontWeight','b')

Example Six: Create Constrained Delaunay Triangulation of Geographical Map
Load a map of the perimeter of the conterminous United States. Construct a constrained Delaunay triangulation representing the polygon. This triangulation spans a domain that is bounded by the convex hull of the set of points. Filter out the triangles that are within the domain of the polygon and plot them. Note: The data set contains duplicate data points; that is, two or more datapoints have the same location. The duplicate points are rejected and the delaunayTriangulation reformats the constraints accordingly.
clf
load usapolygonDefine an edge constraint between two successive points that make up the polygonal boundary and create the Delaunay triangulation.
nump = numel(uslon); C = [(1:(nump-1))' (2:nump)'; nump 1]; dt = delaunayTriangulation(uslon,uslat,C);
Warning: Duplicate data points have been detected and removed. The Triangulation indices and constraints are defined with respect to the unique set of points in delaunayTriangulation.
Warning: Intersecting edge constraints have been split, this may have added new points into the triangulation.
io = isInterior(dt); patch('Faces',dt(io,:),'Vertices',dt.Points,'FaceColor','r') axis equal axis([-130 -60 20 55]) xlabel('Constrained Delaunay Triangulation of usapolygon','FontWeight','b')

Example Seven: Curve Reconstruction from Point Cloud
This example highlights the use of a Delaunay triangulation to reconstruct a polygonal boundary from a cloud of points. The reconstruction is based on the elegant Crust algorithm.
Reference: N. Amenta, M. Bern, and D. Eppstein. The crust and the beta-skeleton: combinatorial curve reconstruction. Graphical Models and Image Processing, 60:125-135, 1998.
Create a set of points representing the point cloud.
numpts = 192; t = linspace( -pi, pi, numpts+1 )'; t(end) = []; r = 0.1 + 5*sqrt( cos( 6*t ).^2 + (0.7).^2 ); x = r.*cos(t); y = r.*sin(t); ri = randperm(numpts); x = x(ri); y = y(ri);
Construct a Delaunay Triangulation of the point set.
dt = delaunayTriangulation(x,y); tri = dt(:,:);
Insert the location of the Voronoi vertices into the existing triangulation.
V = voronoiDiagram(dt);
Remove the infinite vertex and filter out duplicate points using unique.
V(1,:) = [];
numv = size(V,1);
dt.Points(end+(1:numv),:) = unique(V,'rows');The Delaunay edges that connect pairs of sample points represent the boundary.
delEdges = edges(dt); validx = delEdges(:,1) <= numpts; validy = delEdges(:,2) <= numpts; boundaryEdges = delEdges((validx & validy),:)'; xb = x(boundaryEdges); yb = y(boundaryEdges); clf triplot(tri,x,y) axis equal hold on plot(x,y,'*r') plot(xb,yb,'-r') xlabel('Curve reconstruction from point cloud','FontWeight','b') hold off

Example Eight: Compute Approximate Medial Axis of Polygonal Domain
This example shows how to create an approximate Medial Axis of a polygonal domain using a constrained Delaunay triangulation. The Medial Axis of a polygon is defined by the locus of the center of a maximal disk within the polygon interior.
Construct a constrained Delaunay triangulation of a sample of points on the domain boundary.
load trimesh2d
dt = delaunayTriangulation(x,y,Constraints);
inside = isInterior(dt);Construct a triangulation to represent the domain triangles.
tr = triangulation(dt(inside,:),dt.Points);
Construct a set of edges that join the circumcenters of neighboring triangles. The additional logic constructs a unique set of such edges.
numt = size(tr,1); T = (1:numt)'; neigh = neighbors(tr); cc = circumcenter(tr); xcc = cc(:,1); ycc = cc(:,2); idx1 = T < neigh(:,1); idx2 = T < neigh(:,2); idx3 = T < neigh(:,3); neigh = [T(idx1) neigh(idx1,1); T(idx2) neigh(idx2,2); T(idx3) neigh(idx3,3)]';
Plot the domain triangles in green, the domain boundary in blue, and the medial axis in red.
clf triplot(tr,'g') hold on plot(xcc(neigh), ycc(neigh), '-r','LineWidth',1.5) axis([-10 310 -10 310]) axis equal plot(x(Constraints'),y(Constraints'),'-b','LineWidth',1.5) xlabel('Medial Axis of Polygonal Domain','FontWeight','b') hold off

Example Nine: Morph 2-D Mesh to Modified Boundary
This example shows how to morph a mesh of a 2-D domain to accommodate a modification to the domain boundary.
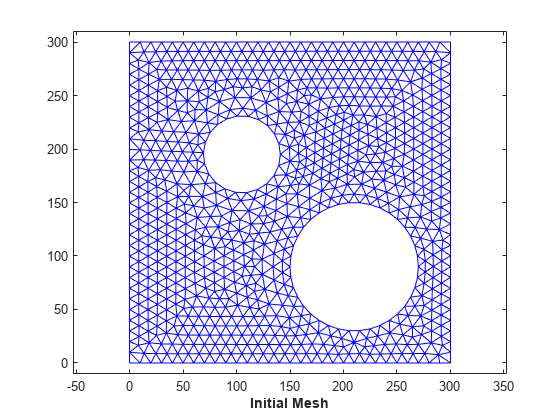
Step 1: Load the data. The mesh to be morphed is defined by trife, xfe, and yfe, which is a triangulation in face-vertex format.
load trimesh2d clf triplot(trife,xfe,yfe) axis equal axis([-10 310 -10 310]) axis equal xlabel('Initial Mesh','FontWeight','b')
Step 2: Construct a background triangulation - a Constrained Delaunay triangulation of the set of points representing the mesh boundary. For each vertex of the mesh, compute a descriptor that defines its location with respect to the background triangulation. The descriptor is the enclosing triangle together with the barycentric coordinates with respect to that triangle.
dt = delaunayTriangulation(x,y,Constraints); clf triplot(dt) axis equal axis([-10 310 -10 310]) axis equal xlabel('Background Triangulation','FontWeight','b')

descriptors.tri = pointLocation(dt,xfe,yfe); descriptors.baryCoords = cartesianToBarycentric(dt,descriptors.tri,[xfe yfe]);
Step 3: Edit the background triangulation to incorporate the desired modification to the domain boundary.
cc1 = [210 90]; circ1 = (143:180)'; x(circ1) = (x(circ1)-cc1(1))*0.6 + cc1(1); y(circ1) = (y(circ1)-cc1(2))*0.6 + cc1(2); tr = triangulation(dt(:,:),x,y); clf triplot(tr) axis([-10 310 -10 310]) axis equal xlabel('Edited Background Triangulation - Hole Size Reduced','FontWeight','b')

Step 4: Convert the descriptors back to Cartesian coordinates using the deformed background triangulation as a basis for evaluation.
Xnew = barycentricToCartesian(tr,descriptors.tri,descriptors.baryCoords); tr = triangulation(trife,Xnew); clf triplot(tr) axis([-10 310 -10 310]) axis equal xlabel('Morphed Mesh','FontWeight','b')
