Multidomain Geometry Reconstructed from Mesh

This example shows how to split a single-domain block geometry into two domains. The first part of the example generates a mesh and divides the mesh elements into two groups. The second part of the example creates a two-domain geometry based on this division.

Generate Mesh and Split Its Elements into Two Groups

Create a block geometry.

gmSingleDomain = fegeometry("Block.stl");

Generate and plot a mesh.

gmSingleDomain = generateMesh(gmSingleDomain);

figure
pdemesh(gmSingleDomain)

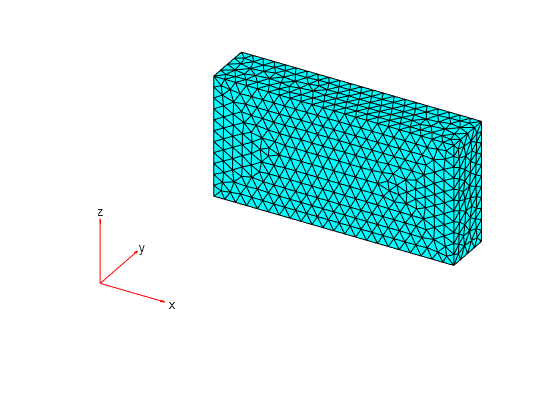
Obtain the nodes and elements of the mesh.

msh = gmSingleDomain.Mesh;
nodes = msh.Nodes;
elements = msh.Elements;

Find the x-coordinates of the geometric centers of all elements of the mesh. First, create an array of the same size as elements that contains the x-coordinates of the nodes forming the mesh elements. Each column of this vector contains the x-coordinates of 10 nodes that form an element.

elemXCoords = reshape(nodes(1,elements),10,[]);

Compute the mean of each column of this array to get a vector of the x-coordinates of the element geometric centers.

elemXCoordsGeometricCenter = mean(elemXCoords);

Assume that all elements have the same region ID and create a matrix ElementIdToRegionId.

ElementIdToRegionId = ones(1,size(elements,2));

Find IDs of all elements for which the x-coordinate of the geometric center exceeds 60.

idx = elemXCoordsGeometricCenter > 60;

For the elements with centers located beyond x = 60, change the region IDs to 2.

ElementIdToRegionId(idx) = 2;

Create Geometry with Two Cells

Create a new geometry from the mesh nodes and elements and assign the elements to two cells of the geometry based on their IDs.

gmTwoDomains = fegeometry(nodes',elements',ElementIdToRegionId)

gmTwoDomains = 
  fegeometry with properties:

       NumCells: 2
       NumFaces: 73
       NumEdges: 149
    NumVertices: 79
       Vertices: [79x3 double]
           Mesh: [1x1 FEMesh]

Plot the geometry, displaying the cell labels.

pdegplot(gmTwoDomains,CellLabels="on",FaceAlpha=0.5)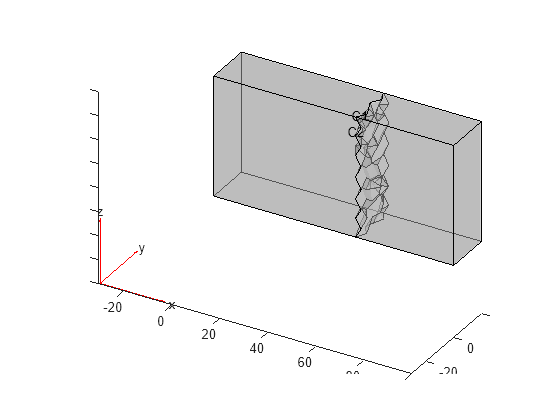

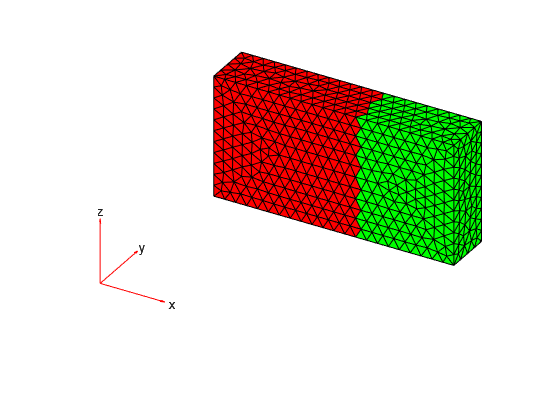
Highlight the elements from cell 1 in red and the elements from cell 2 in green.

elementIDsCell1 = findElements(gmTwoDomains.Mesh,"region",Cell=1);
elementIDsCell2 = findElements(gmTwoDomains.Mesh,"region",Cell=2);

figure
pdemesh(gmTwoDomains.Mesh.Nodes, ...
        gmTwoDomains.Mesh.Elements(:,elementIDsCell1), ...
        FaceColor="red")
hold on
pdemesh(gmTwoDomains.Mesh.Nodes, ...
        gmTwoDomains.Mesh.Elements(:,elementIDsCell2), ...
        FaceColor="green")

When you divide mesh elements into groups and then create a multidomain geometry based on this division, the mesh might be invalid for the multidomain geometry. For example, elements in a cell might be touching by only a node or an edge instead of sharing a face. In this case, fegeometry throws an error saying that neighboring elements in the mesh are not properly connected.