Vehicle Steering Gain at Different Speeds

Open Script

This example shows how to use the vehicle dynamics slowly increasing steering reference application to analyze the impact of the steering angle and speed on vehicle handling. Specifically, you can calculate the steering gain when you run the maneuver with different speed set points. Based on the constant speed, variable steer test defined in SAE J266, the slowly increasing steering maneuver helps characterize the lateral dynamics of the vehicle. In the test, the driver:

Accelerates until vehicle hits a target velocity.
Maintains a target velocity.
Linearly increases the steering wheel angle from 0 degrees to a maximum angle.
Maintains the steering wheel angle for a specified time.
Linearly decreases the steering wheel angle from maximum angle to 0 degrees.

For more information about the reference application, see Slowly Increasing Steering Maneuver.

helpersetupsis;

Run a Slowly Increasing Steering Maneuver

1. Open the Slowly Increasing Steer block. By default, the maneuver is set with these parameters:

Longitudinal speed setpoint — 50 mph
Handwheel rate — 13.5 deg
Maximum handwheel angle — 270 deg

2. In the Visualization subsystem, open the 3D Engine block. By default, the 3D Engine parameter is set to Disabled. Simulating models in the 3D visualization environment requires Simulink® 3D Animation™. For the 3D visualization engine platform requirements and hardware recommendations, see the Unreal Engine Simulation Environment Requirements and Limitations.

3. Run the maneuver with the default settings. As the simulation runs, view the vehicle information.

mdl = 'ISReferenceApplication';
sim(mdl);

### Starting serial model reference simulation build.
### Model reference simulation target for Driveline is up to date.
### Model reference simulation target for PassVeh14DOF is up to date.
### Model reference simulation target for SiMappedEngineV is up to date.

Build Summary

0 of 3 models built (3 models already up to date)
Build duration: 0h 0m 8.9207s
GearState =
     2

GearState =
     3

GearState =
     4

GearState =
     5

GearState =
     6

GearState =
     6

In the Vehicle Position window, view the vehicle longitudinal distance as a function or the lateral distance. The yellow line displays the yaw rate. The blue line shows the steering angle.

In the Visualization subsystem, open the Yaw Rate and Steer Scope block to display the yaw rate and steering angle versus time.

Sweep Speed Set Points

Run the slowly increasing steering angle reference application with three different speed set points.

1. In the slowly increasing steering reference application model ISReferenceApplication, open the Slowly Increasing Steer block. The Longitudinal speed set point, xdot_r block parameter sets the vehicle speed. By default, the speed is 50 mph.

2. Enable signal logging for the velocity, lane, and ISO signals. You can use the Simulink® editor or, alternatively, these MATLAB® commands. Save the model.

Enable signal logging for the Slowly Increasing Steer Ref signal outport.

mdl = 'ISReferenceApplication';
ph=get_param('ISReferenceApplication/Slowly Increasing Steer','PortHandles');
set_param(ph.Outport(1),'DataLogging','on');

Enable signal logging for the Passenger Vehicle block outport signal.

ph=get_param('ISReferenceApplication/Passenger Vehicle','PortHandles');
set_param(ph.Outport(1),'DataLogging','on');

In the Visualization subsystem, enable signal logging for the ISO block.

set_param([mdl '/Visualization/ISO 15037-1:2006'],'Measurement','Enable');

3. Set up a speed set point vector, xdot_r, that you want to investigate. For example, at the command line, type:

vmax = [45, 50, 55];
numExperiments = length(vmax);

4. Create an array of simulation inputs that set the Slowly Increasing Steer block parameter Longitudinal speed setpoint, xdot_r equal to xdot_r.

for idx = numExperiments:-1:1
    in(idx) = Simulink.SimulationInput(mdl);
    in(idx) = in(idx).setBlockParameter([mdl '/Slowly Increasing Steer'], ...
        'xdot_r', num2str(vmax(idx)));
end

5. Save the model and run the simulations. If available, use parallel computing.

save_system(mdl)
tic;
simout = parsim(in,'ShowSimulationManager','on');
toc;

[27-Sep-2023 08:30:32] Checking for availability of parallel pool...
[27-Sep-2023 08:30:32] Starting Simulink on parallel workers...
[27-Sep-2023 08:30:36] Loading project on parallel workers...
[27-Sep-2023 08:30:36] Configuring simulation cache folder on parallel workers...
[27-Sep-2023 08:30:36] Loading model on parallel workers...
[27-Sep-2023 08:30:54] Running simulations...
[27-Sep-2023 08:32:15] Completed 1 of 3 simulation runs
[27-Sep-2023 08:32:16] Completed 2 of 3 simulation runs
[27-Sep-2023 08:32:17] Completed 3 of 3 simulation runs
[27-Sep-2023 08:32:17] Cleaning up parallel workers...
Elapsed time is 117.882577 seconds.

6. After the simulations complete, close the Simulation Data Inspector windows.

Use Simulation Data Inspector to Analyze Results

Use the Simulation Data Inspector to examine the results. You can use the UI or, alternatively, command-line functions.

1. Open the Simulation Data Inspector. On the Simulink Toolstrip, on the Simulation tab, under Review Results, click Data Inspector.

In the Simulation Data Inspector, select Import.

In the Import dialog box, clear logsout. Select simout(1), simout(2), and simout(3). Select Import.

Use the Simulation Data Inspector to examine the results.

2. Alternatively, use these MATLAB commands to plot the longitudinal velocity, steering wheel angle, lateral acceleration, longitudinal position, and lateral position.

for idx = 1:numExperiments
    % Create sdi run object
    simoutRun(idx)=Simulink.sdi.Run.create;
    simoutRun(idx).Name=['Velocity = ', num2str(vmax(idx))];
    add(simoutRun(idx),'vars',simout(idx));
end
sigcolor=[0 1 0;0 0 1;1 0 1];
for idx = 1:numExperiments
    % Extract the lateral acceleration, position, and steering
    msignal(idx)=getSignalsByName(simoutRun(idx), 'xdot_mph');
    msignal(idx).LineColor =sigcolor((idx),:);
    ssignal(idx)=getSignalsByName(simoutRun(idx), 'SteerAngle');
    ssignal(idx).LineColor =sigcolor((idx),:);
    asignal(idx)=getSignalsByName(simoutRun(idx), 'Lateral acceleration');
    asignal(idx).LineColor =sigcolor((idx),:);
    xsignal(idx)=getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.InertFrm.Cg.Disp.X');
    xsignal(idx).LineColor =sigcolor((idx),:);
    ysignal(idx)=getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.InertFrm.Cg.Disp.Y');
    ysignal(idx).LineColor =sigcolor((idx),:);
end
Simulink.sdi.view
Simulink.sdi.setSubPlotLayout(5,1);
for idx = 1:numExperiments
    % Plot the lateral position, steering angle, and lateral acceleration
    plotOnSubPlot(msignal(idx),1,1,true);
    plotOnSubPlot(ssignal(idx),2,1,true);
    plotOnSubPlot(asignal(idx),3,1,true);
    plotOnSubPlot(xsignal(idx),4,1,true);
    plotOnSubPlot(ysignal(idx),5,1,true);
end

The results are similar to these plots, which indicate that the greatest lateral acceleration occurs when the vehicle velocity is 45 mph.

Further Analysis

To explore the results further, use these commands to extract the lateral acceleration, steering angle, and vehicle trajectory from the simout object.

1. Extract the lateral acceleration and steering angle. Plot the data. The results are similar to this plot.

figure
for idx = 1:numExperiments
    % Extract Data
    log = get(simout(idx),'logsout');
    sa=log.get('Steering-wheel angle').Values;
    ay=log.get('Lateral acceleration').Values;
    firstorderfit = polyfit(sa.Data,ay.Data,1);
    gain(idx)=firstorderfit(1);
    legend_labels{idx} = [num2str(vmax(idx)), ' mph: Gain = ', ...
        num2str(gain(idx)), ' m/(deg s^2)'];
    % Plot steering angle vs. lateral acceleration
    plot(sa.Data,ay.Data)
    hold on
end
% Add labels to the plots
legend(legend_labels, 'Location', 'best');
title('Lateral Acceleration')
xlabel('Steering Angle [deg]')
ylabel('Acceleration [m/s^2]')
grid on

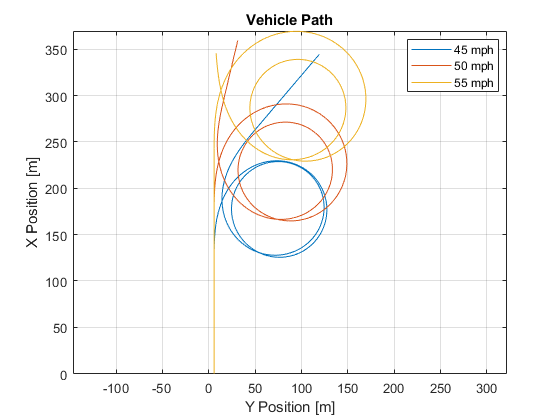
2. Extract the vehicle path. Plot the data. The results are similar to this plot.

figure
for idx = 1:numExperiments
    % Extract Data
    log = get(simout(idx),'logsout');
    xValues = getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.InertFrm.Cg.Disp.X').Values;
    yValues = getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.InertFrm.Cg.Disp.Y').Values;
    x = xValues.Data;
    y = yValues.Data;
    legend_labels{idx} = [num2str(vmax(idx)), ' mph'];
    % Plot vehicle location
    axis('equal')
    plot(y,x)
    hold on
end
% Add labels to the plots
legend(legend_labels, 'Location', 'best');
title('Vehicle Path')
xlabel('Y Position [m]')
ylabel('X Position [m]')
grid on

References

[1] SAE J266. Steady-State Directional Control Test Procedures For Passenger Cars and Light Trucks. Warrendale, PA: SAE International, 1996.