gffilter (prime Galois field)
Filter data using polynomials over prime Galois field
Syntax
y = gffilter(b,a,x)
y = gffilter(b,a,x,p)
Description
Note
This function performs computations in GF(pm), where p is prime.
To work in GF(2m), use the filter function with
Galois arrays. For details, see Filtering.
y = gffilter(b,a,x) filters the data in vector
x with the filter described by vectors b and
a. The vectors b, a and
x must be in GF(2), that is, be binary and y is also in
GF(2).
y = gffilter(b,a,x,p) filters the data
x using the filter described by vectors a and
b. y is the filtered data in GF(p).
p is a prime number, and all entries of a and
b are between 0 and p-1.
By definition of the filter, y solves the difference equation
a(1)y(n) = b(1)x(n)+b(2)x(n-1)+b(3)x(n-2)+...+b(B+1)x(n-B) -a(2)y(n-1)-a(3)y(n-2)-...-a(A+1)y(n-A)
where
A+1 is the length of the vectoraB+1 is the length of the vectorbnvaries between 1 and the length of the vectorx.
The vector a represents the degree-na polynomial
a(1)+a(2)x+a(3)x^2+...+a(A+1)x^A
Examples
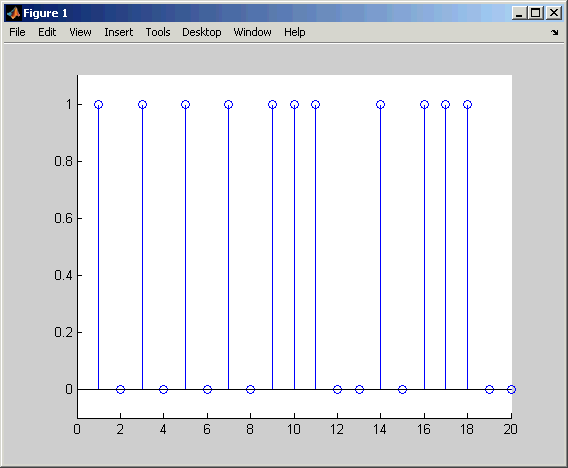
The impulse response of a particular filter is given in the code and diagram below.
b = [1 0 0 1 0 1 0 1]; a = [1 0 1 1]; y = gffilter(b,a,[1,zeros(1,19)]); stem(y); axis([0 20 -.1 1.1])
Version History
Introduced before R2006a