OVSF Code Generator
Generate OVSF code
Libraries:
Communications Toolbox /
Comm Sources /
Sequence Generators
Description
The OVSF Code Generator block generates a code from an orthogonal variable spreading factor (OVSF) matrix. Use OVSF codes to preserve orthogonality between different channels in a spread spectrum communications system. For more information, see Algorithms.
Examples
Generate 10 samples of an OVSF code with a spreading factor of 32.
The cm_generate_ovsf_code model sets Code length to 32, Code index to 12, and Samples per frame to 10. Other parameters use the default settings.

Run the model and display the generated OVSF code.
ans =
1
1
-1
-1
-1
-1
1
1
1
1
Ports
Output
Output data, returned as a binary-valued column vector containing the OVSF code generated from a set of orthogonal codes.
Data Types: double | int8
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Length of the generated code, specified as a positive integer power of 2. The code length value is the spreading factor of the code. For more information, see Spread Spectrum.
The spreading factor is the length of the code selected from the OVSF code matrix. OVSF codes are defined as the rows of an N-by-N matrix, CN. The Code index parameter specifies the row of the CN matrix as the code of interest. For more information, see Orthogonal Variable Spreading Factor Codes.
Row index of the OVSF code matrix, specified as an integer in the range [0, (N – 1)], where N is the spreading factor as specified by the value of the Code length parameter. OVSF codes are defined as the rows of an N-by-N matrix, CN. The value of this property specifies the row of the CN matrix as the code of interest. For more information, see Recovering and Reconstructing OVSF Codes.
Positive scalars specify the time in seconds between each
sample of the output signal. If you set the sample time to -1, the output
signal inherits the sample time from downstream. For information on the relationship between the
Sample time and Samples per frame parameters,
see
Sample Timing.
Number of OVSF code chips output, specified as a positive integer. Each time the block runs, it outputs the first Samples per frame chips of the OVSF code specified by the Code length and Code index property values. For more information, see Spread Spectrum.
For information on the relationship between Sample time and Samples per frame, see Sample Timing.
Output data type, specified as double or
int8.
Type of simulation to run, specified as Code generation or
Interpreted execution.
Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option shortens startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
The time between output updates is equal to the product of the
Samples per frame and Sample time parameter
values. For example, if Sample time and Samples per
frame each equal 1, the block outputs one sample every
second. If you increase Samples per frame to 10, then the block outputs
a 10-by-1 vector every 10 seconds. This timing ensures that the equivalent output rate is
not dependent on the Samples per frame parameter.
Algorithms
As discussed in [1], OVSF codes were first introduced for 3G communication systems and are primarily used to preserve orthogonality between different channels in a spread spectrum communications system.
OVSF codes with spreading factor N of an N-by-N OVSF code matrix, CN, are the individual rows of an N-by-N matrix, CN, which is defined recursively. First, define C1 = [1]. Next, assume that CN is defined and let CN(k) denote the kth row of CN. Define C2N by
CN is defined for N only as a nonnegative power of 2. It follows by induction that the rows of CN are orthogonal.
The OVSF codes can also be defined recursively by a tree structure.
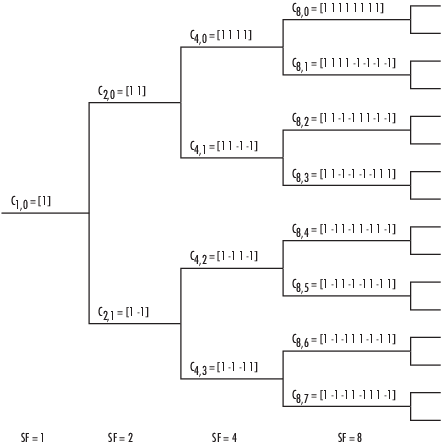
If [C] has a code length 2r at depth r in the tree, where the root has depth 0, the two branches leading out of C are labeled by the sequences [C C] and [C –C], which have length 2r+1. The codes at depth r in the tree are the rows of the matrix CN, where N = 2r.
Two OVSF codes are orthogonal if and only if neither code lies on the path from the other code to the root. Since codes assigned to different users in the same cell must be orthogonal, this requirement restricts the number of available codes for a given cell. For example, if the code C41 in the tree is assigned to a user, the codes C10, C20, C82, C83, and so on cannot be assigned to any other user in the same cell.
To select the OVSF code to output, you specify the spreading factor and the code index. The code index specifies how far down the column of the tree at depth r the code appears. For CN, k in the tree structure diagram, N is the spreading factor and k is the code index. The code index must be an integer in the range [0, N – 1]. If the code appears at depth r in the tree structure, the spreading factor is 2r.
To recover the code, based on the spreading factor and the code index:
Convert the code index to the corresponding binary number.
Add 0s to the left, if necessary, so that the resulting binary sequence x1 x2 ... xr has length r, where r is the logarithm base 2 of the spreading factor. This binary sequence describes the path from the root to the code.
The path takes the upper branch from the code at depth i if xi = 0, and the lower branch if xi = 1.
To reconstruct the code, recursively define a sequence of codes Ci:
Let C0 be the root [1].
Assuming that Ci has been defined, for i < r, define Ci+1 by
The code CN has the specified spreading factor and code index.
For example, to find the code with spreading factor 16 and code index 6, do the following:
Convert 6 to the binary number 110.
Add one 0 to the left to obtain 0110, which has length 4 = log2(16).
Construct the sequences Ci according to the following table.
i xi Ci 0 C0 = [1]
1 0 C1 = C0 C0 = [1] [1]
2 1 C2 = C1 –C1 = [1 1] [–1 –1]
3 1 C3 = C2 -C2 = [1 1 –1 –1] [–1 –1 1 1]
4 0 C4 = C3 C3 = [1 1 –1 –1 –1 –1 1 1] [1 1 –1 –1 –1 –1 1 1]
The code C4 has spreading factor 16 and code index 6.
In general, spread spectrum multiplies each data message sample by a coded set of chips. To avoid confusion with samples of the data message, the term chips refers to samples or bits of a code used to spread data over a wide spectrum in digital communications. The length of the code is the spreading factor.
The spreading factor, SF = Rchip/Rdata,
Rchip is the chip rate. The chip rate of a code is the number of chips per second transmitted or received. Multiple chips represent each data sample because the spreading factor must be a positive power of 2 that is greater than 1.
Rdata is the sample rate of the message data.
References
[1] Kasapović, S. and N. Sarajlić. "OVSF code assignment in UMTS networks." 2010 20th International Crimean Conference "Microwave & Telecommunication Technology", 429–32. Sevastopol: IEEE®, 2010. https://doi.org/10.1109/CRMICO.2010.5632706.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006aStarting in R2020a, Simulink no longer allows you to use the OVSF Code Generator block version available before R2015b.
Existing models automatically update to load the OVSF Code Generator block version announced in Source blocks output frames of contiguous time samples but do not use frame attribute. For more information on block forwarding, see Maintain Compatibility of Library Blocks Using Forwarding Tables (Simulink).
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)