LTI System
Use linear time invariant system model object in Simulink
Libraries:
Control System Toolbox
Description
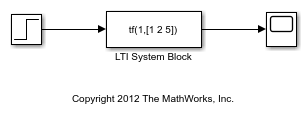
The LTI System block imports linear system model objects into the
Simulink® environment. You specify the LTI model to import in the LTI
system variable parameter. You can import any type of proper linear
time-invariant dynamic system model. If the imported system is a state-space (ss) model, you can specify initial state values in the Initial
states parameter.