designMultistageInterpolator
Multistage interpolator design
Syntax
Description
C = designMultistageInterpolator(L)L. In order for C to be multistage,
L must not be a prime number. For details, see Algorithms. The design process can
take a while if L has many factors.
C = designMultistageInterpolator(L,Fs,TW)Fs and a
transition width of TW. Sampling rate in this case refers to the output
sampling rate of the signal after the multistage interpolator.
The multistage interpolator has a cutoff frequency of Fs/2.
C = designMultistageInterpolator(___,Name=Value)
Example: C =
designMultistageInterpolator(48,48000,200,80,NumStages='auto') designs a
multistage interpolator with the least number of multiplications per input sample
(MPIS).
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
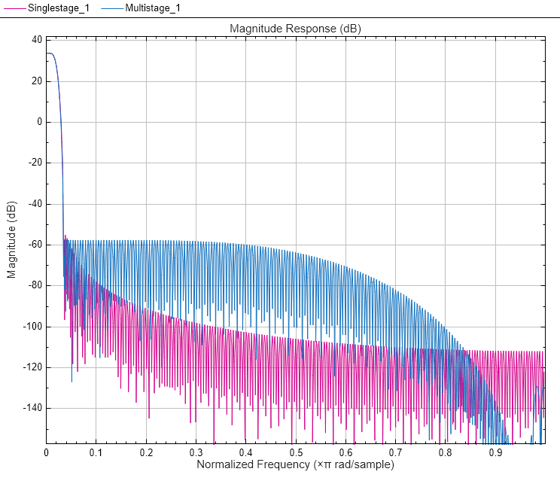
The overall interpolation factor is split into smaller factors with each factor being the interpolation factor of the corresponding individual stage. The combined interpolation of all the individual stages must equal the overall interpolation. The combined response must meet or exceed the given design specifications.
The function determines the number of interpolator stages through the
NumStages argument. The sequence of stages is determined based on the
implementation cost. By default, NumStages is set to
'auto', resulting in a sequence that gives the lowest number of MPIS.
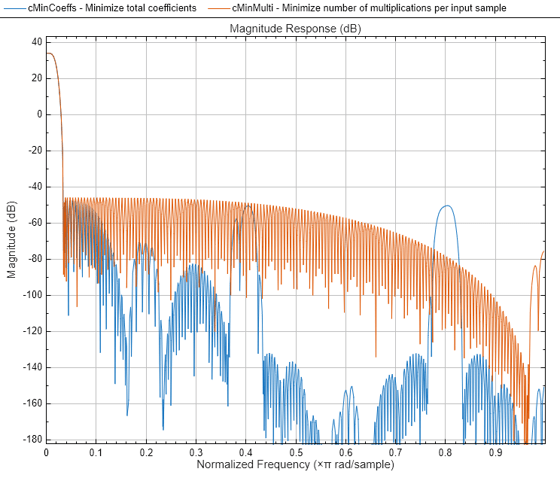
When multiple configurations result in the same lowest MPIS within the tolerance specified,
the configuration that yields the lowest number of coefficients overall is chosen. If
MinTotalCoeffs is set to true, the function
determines the sequence that requires the lowest number of total coefficients.
By default, the CostMethod is set to 'estimate'.
In this mode, the function estimates the filter order required for each stage and designs the
filter based on the estimate. This method is faster but can lead to suboptimal designs. For an
optimal design, set CostMethod to 'design'. In this
mode, the function designs each stage and computes the filter order.