fdesign.arbmag
Arbitrary response magnitude filter specification object
Syntax
D= fdesign.arbmag
D= fdesign.arbmag(SPEC)
D = fdesign.arbmag(SPEC,specvalue1,specvalue2,...)
D = fdesign.arbmag(specvalue1,specvalue2,specvalue3)
D = fdesign.arbmag(...,Fs)
Description
D= fdesign.arbmag constructs
an arbitrary magnitude filter specification object D.
D= fdesign.arbmag(SPEC) initializes
the Specification property to SPEC.
The input argument SPEC must be one of the entries
shown in the following table. Specification entries are not case sensitive.
Note
Specification entries marked with an asterisk require the DSP System Toolbox™ software.
'N,F,A'— Single band design (default)'F,A,R'— Single band minimum order design *'N,B,F,A'— Multiband design'N,B,F,A,C'— Constrained multiband design *'B,F,A,R'— Multiband minimum order design *'Nb,Na,F,A'— Single band design *'Nb,Na,B,F,A'— Multiband design *
The SPEC entries are defined as follows:
A— Amplitude vector. Values inAdefine the filter amplitude at frequency points you specify inf, the frequency vector. If you useA, you must useFas well. Amplitude values must be real. For complex values designs, usefdesign.arbmagnphase.B— Number of bands in the multiband filterC— Constrained band flag. This enables you to constrain the passband ripple in your multiband design. You cannot constrain the passband ripple in all bands simultaneously.F— Frequency vector. Frequency values in specified inFindicate locations where you provide specific filter response amplitudes. When you provideF, you must also provideA.N— Filter order for FIR filters and the numerator and denominator orders for IIR filters.Nb— Numerator order for IIR filtersNa— Denominator order for IIR filter designsR— Ripple
By default, this method assumes that all frequency specifications are supplied in normalized frequency.
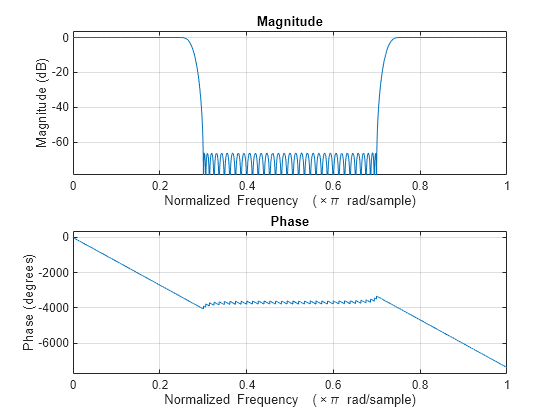
Specifying Frequency and Amplitude Vectors
F and A are the input
arguments you use to define the filter response desired. Each frequency
value you specify in F must have a corresponding
response value in A. The following table shows
how F and A are related.
Define the frequency vector F as [0
0.25 0.3 0.4 0.5 0.6 0.7 0.75 1.0]
Define the response vector A as [1
1 0 0 0 0 0 1 1]
These specifications connect F and A as
shown here:
F (Normalized Frequency) | A (Response Desired at F) |
|---|---|
0 | 1 |
0.25 | 1 |
0.3 | 0 |
0.4 | 0 |
0.5 | 0 |
0.6 | 0 |
0.7 | 0 |
0.75 | 1 |
1.0 | 1 |
Different specifications can have different design methods available.
Use designmethods to get a
list of design methods available for a given specification and filter
specification object.
Use designopts to get
a list of design options available for a filter specification object
and a given design method. Enter help(D,METHOD) to
get detailed help on the available design options for a given design
method.
D = fdesign.arbmag(SPEC,specvalue1,specvalue2,...) initializes
the specifications with specvalue1, specvalue2.
Use get(D,'Description') for descriptions of the
various specifications specvalue1, specvalue2,
... specvalueN.
D = fdesign.arbmag(specvalue1,specvalue2,specvalue3) uses
the default specification 'N,F,A', setting the
filter order, filter frequency vector, and the amplitude vector to
the values specvalue1, specvalue2,
and specvalue3.
D = fdesign.arbmag(...,Fs) specifies
the sampling frequency in Hz. All other frequency specifications are
also assumed to be in Hz when you specify Fs.
Examples
Version History
Introduced in R2009a