infer
Infer vector error-correction (VEC) model innovations
Description
Tbl2 = infer(Mdl,Tbl1)Tbl2 containing the multivariate
residuals from evaluating the fully specified VEC(p – 1) model
Mdl at the response variables in the table or timetable of
data Tbl1. (since R2022b)
infer selects the variables in Mdl.SeriesNames or all variables in Tbl1. To select different response variables in Tbl1 at which to evaluate the model, use the ResponseVariables name-value argument.
___ = infer(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name,Value)infer returns the output argument combination for the
corresponding input arguments. For example, infer(Mdl,Y,Y0=PS,X=Exo) computes the
residuals of the VEC(p – 1) model Mdl at the
matrix of response data Y, and specifies the matrix of presample
response data PS and the matrix of exogenous predictor data
Exo.
Supply all input data using the same data type. Specifically:
If you specify the numeric matrix
Y, optional data sets must be numeric arrays and you must use the appropriate name-value argument. For example, to specify a presample, set theY0name-value argument to a numeric matrix of presample data.If you specify the table or timetable
Tbl1, optional data sets must be tables or timetables, respectively, and you must use the appropriate name-value argument. For example, to specify a presample, set thePresamplename-value argument to a table or timetable of presample data.
Examples
Consider a VEC model for the following seven macroeconomic series, and then fit the model to a matrix of response data.
Gross domestic product (GDP)
GDP implicit price deflator
Paid compensation of employees
Nonfarm business sector hours of all persons
Effective federal funds rate
Personal consumption expenditures
Gross private domestic investment
Suppose that a cointegrating rank of 4 and one short-run term are appropriate, that is, consider a VEC(1) model.
Load the Data_USEconVECModel data set.
load Data_USEconVECModelFor more information on the data set and variables, enter Description at the command line.
Determine whether the data needs to be preprocessed by plotting the series on separate plots.
figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.GDP) title("Gross Domestic Product") ylabel("Index") xlabel("Date") nexttile plot(FRED.Time,FRED.GDPDEF) title("GDP Deflator") ylabel("Index") xlabel("Date") nexttile plot(FRED.Time,FRED.COE) title("Paid Compensation of Employees") ylabel("Billions of $") xlabel("Date") nexttile plot(FRED.Time,FRED.HOANBS) title("Nonfarm Business Sector Hours") ylabel("Index") xlabel("Date")

figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.FEDFUNDS) title("Federal Funds Rate") ylabel("Percent") xlabel("Date") nexttile plot(FRED.Time,FRED.PCEC) title("Consumption Expenditures") ylabel("Billions of $") xlabel("Date") nexttile plot(FRED.Time,FRED.GPDI) title("Gross Private Domestic Investment") ylabel("Billions of $") xlabel("Date")
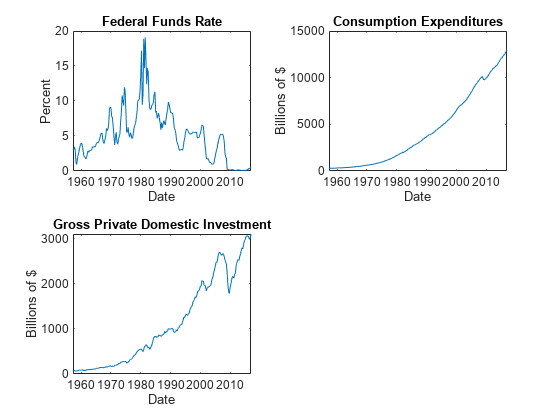
Stabilize all series, except the federal funds rate, by applying the log transform. Scale the resulting series by 100 so that all series are on the same scale.
FRED.GDP = 100*log(FRED.GDP); FRED.GDPDEF = 100*log(FRED.GDPDEF); FRED.COE = 100*log(FRED.COE); FRED.HOANBS = 100*log(FRED.HOANBS); FRED.PCEC = 100*log(FRED.PCEC); FRED.GPDI = 100*log(FRED.GPDI);
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = FRED.Properties.VariableNames
Mdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model with Linear Time Trend"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [7×1 vector of NaNs]
Adjustment: [7×4 matrix of NaNs]
Cointegration: [7×4 matrix of NaNs]
Impact: [7×7 matrix of NaNs]
CointegrationConstant: [4×1 vector of NaNs]
CointegrationTrend: [4×1 vector of NaNs]
ShortRun: {7×7 matrix of NaNs} at lag [1]
Trend: [7×1 vector of NaNs]
Beta: [7×0 matrix]
Covariance: [7×7 matrix of NaNs]
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Estimate the model by supplying a matrix of data. Use default options.
EstMdl = estimate(Mdl,FRED.Variables)
EstMdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [14.1329 8.77841 -7.20359 ... and 4 more]'
Adjustment: [7×4 matrix]
Cointegration: [7×4 matrix]
Impact: [7×7 matrix]
CointegrationConstant: [-28.6082 -109.555 77.0912 ... and 1 more]'
CointegrationTrend: [4×1 vector of zeros]
ShortRun: {7×7 matrix} at lag [1]
Trend: [7×1 vector of zeros]
Beta: [7×0 matrix]
Covariance: [7×7 matrix]
EstMdl is an estimated vecm model object. It is fully specified because all parameters have known values. By default, estimate imposes the constraints of the H1 Johansen VEC model form by removing the cointegrating trend and linear trend terms from the model. Parameter exclusion from estimation is equivalent to imposing equality constraints to zero.
Infer innovations from the estimated model, the residuals from the model fit. Supply the matrix of in-sample data.
E = infer(EstMdl,FRED.Variables);
E is a 238-by-7 matrix of inferred innovations. Columns correspond to the variable names in EstMdl.SeriesNames.
Alternatively, you can return residuals when you call estimate by supplying an output variable in the fourth position.
Plot the residuals on separate plots. Synchronize the residuals with the dates by removing the first EstMdl.P dates.
idx = FRED.Time((EstMdl.P + 1):end); titles = "Residuals: " + EstMdl.SeriesNames; figure tiledlayout(2,2) for j = 1:4 nexttile plot(idx,E(:,j)) hold on yline(0,"r--") hold off title(titles(j)) end

figure tiledlayout(2,2) for j = 5:7 nexttile plot(idx,E(:,j)) hold on yline(0,"r--") hold off title(titles(j)) end
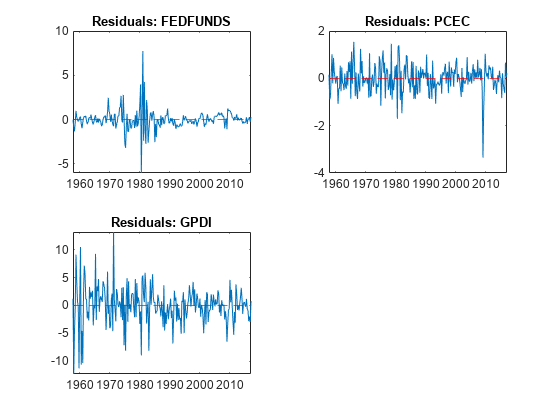
The residuals corresponding to the federal funds rate exhibit heteroscedasticity.
Since R2022b
Consider a VEC model for the following seven macroeconomic series, and then fit the model to a timetable of response data. This example is based on Infer VEC Model Innovations From Matrix of Response Data.
Load and Preprocess Data
Load the Data_USEconVECModel data set.
load Data_USEconVECModel
DTT = FRED;
DTT.GDP = 100*log(DTT.GDP);
DTT.GDPDEF = 100*log(DTT.GDPDEF);
DTT.COE = 100*log(DTT.COE);
DTT.HOANBS = 100*log(DTT.HOANBS);
DTT.PCEC = 100*log(DTT.PCEC);
DTT.GPDI = 100*log(DTT.GPDI);Prepare Timetable for Estimation
When you plan to supply a timetable directly to estimate, you must ensure it has all the following characteristics:
All selected response variables are numeric and do not contain any missing values.
The timestamps in the
Timevariable are regular, and they are ascending or descending.
Remove all missing values from the table.
DTT = rmmissing(DTT); numobs = height(DTT)
numobs = 240
DTT does not contain any missing values.
Determine whether the sampling timestamps have a regular frequency and are sorted.
areTimestampsRegular = isregular(DTT,"quarters")areTimestampsRegular = logical
0
areTimestampsSorted = issorted(DTT.Time)
areTimestampsSorted = logical
1
areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Macroeconomic series in this example are timestamped at the end of the month. This quality induces an irregularly measured series.
Remedy the time irregularity by shifting all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create Model Template for Estimation
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames;
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Fit Model to Data
Estimate the model by supplying the timetable of data DTT. By default, because the number of variables in Mdl.SeriesNames is the number of variables in DTT, estimate fits the model to all the variables in DTT.
EstMdl = estimate(Mdl,DTT);
EstMdl is an estimated vecm model object.
Compute Residuals
Infer innovations from the estimated model, the residuals from the model fit. Supply the timetable of in-sample data DTT. By default, because the number of variables in Mdl.SeriesNames is the number of variables in DTT, infer selects all the variables in DTT, from which to compute residuals.
Tbl = infer(EstMdl,DTT); head(Tbl)
Time GDP GDPDEF COE HOANBS FEDFUNDS PCEC GPDI GDP_Residuals GDPDEF_Residuals COE_Residuals HOANBS_Residuals FEDFUNDS_Residuals PCEC_Residuals GPDI_Residuals
___________ ______ ______ ______ ______ ________ ______ ______ _____________ ________________ _____________ ________________ __________________ ______________ ______________
01-Jul-1957 617.44 281.55 558.01 399.59 3.47 566.71 437.32 0.12076 0.090979 -0.31114 -0.47341 -0.013177 0.14899 1.1764
01-Oct-1957 616.48 281.61 557.48 397.5 2.98 567.26 426.27 -2.4005 -0.39287 -2.1158 -2.1552 -0.86464 -0.89017 -12.289
01-Jan-1958 614.93 282.68 556.15 395.21 1.2 567.09 420.02 -2.0142 0.92195 -1.5874 -1.1852 -1.3247 -0.72797 -4.4964
01-Apr-1958 615.87 282.97 556.03 393.76 0.93 568.09 417.59 0.2131 -0.39586 -0.22658 -0.070487 -0.24993 0.17697 -0.31486
01-Jul-1958 618.76 283.57 558.99 394.95 1.76 569.81 427.67 2.0866 0.45876 2.4738 1.9098 0.98197 1.0195 9.119
01-Oct-1958 621.54 284.04 560.84 396.43 2.42 571.11 438.2 0.68671 0.053454 0.48556 0.63518 0.23659 -0.21548 4.2428
01-Jan-1959 623.66 284.31 563.55 398.35 2.8 573.62 442.12 0.39546 -0.066055 0.97292 1.0224 -0.054929 0.86153 0.68805
01-Apr-1959 626.19 284.46 565.91 400.24 3.39 575.54 449.31 0.24314 -0.22217 0.33889 0.4216 -0.20457 0.26963 -0.15985
size(Tbl)
ans = 1×2
238 14
Tbl is a 238-by-14 timetable of in-sample data in DTT and estimated model residuals. Residual variables names are appended with _Residuals, for example, GDP_Residuals.
Alternatively, you can return residuals when you call estimate by supplying an output variable in the fourth position.
Since R2022b
Consider the model and data in Infer VEC Model Innovations From Matrix of Response Data.
Load Data
Load the Data_USEconVECModel data set.
load Data_USEconVECModelThe Data_Recessions data set contains the beginning and ending serial dates of recessions. Load this data set. Convert the matrix of date serial numbers to a datetime array.
load Data_Recessions dtrec = datetime(Recessions,ConvertFrom="datenum");
Preprocess Data
Remove the exponential trend from the series, and then scale them by a factor of 100.
DTT = FRED; DTT.GDP = 100*log(DTT.GDP); DTT.GDPDEF = 100*log(DTT.GDPDEF); DTT.COE = 100*log(DTT.COE); DTT.HOANBS = 100*log(DTT.HOANBS); DTT.PCEC = 100*log(DTT.PCEC); DTT.GPDI = 100*log(DTT.GPDI);
Create a dummy variable that identifies periods in which the U.S. was in a recession or worse. Specifically, the variable should be 1 if FRED.Time occurs during a recession, and 0 otherwise. Include the variable with the FRED data.
isin = @(x)(any(dtrec(:,1) <= x & x <= dtrec(:,2))); DTT.IsRecession = double(arrayfun(isin,DTT.Time));
Prepare Timetable for Estimation
Remove all missing values from the table.
DTT = rmmissing(DTT);
To make the series regular, shift all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create Model Template for Estimation
Create a VEC(1) model using the shorthand syntax. Assume that the appropriate cointegration rank is 4. You do not have to specify the presence of a regression component when creating the model. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames(1:end-1);
Fit Model to Data
Estimate the model using the entire sample. Specify the predictor identifying whether the observation was measured during a recession.
EstMdl = estimate(Mdl,DTT,PredictorVariables="IsRecession");Compute Residuals
Infer innovations from the estimated model. Supply the predictor data. Return the loglikelihood objective function value.
[Tbl,logL] = infer(EstMdl,DTT,PredictorVariables="IsRecession");
head(Tbl) Time GDP GDPDEF COE HOANBS FEDFUNDS PCEC GPDI IsRecession GDP_Residuals GDPDEF_Residuals COE_Residuals HOANBS_Residuals FEDFUNDS_Residuals PCEC_Residuals GPDI_Residuals
___________ ______ ______ ______ ______ ________ ______ ______ ___________ _____________ ________________ _____________ ________________ __________________ ______________ ______________
01-Jul-1957 617.44 281.55 558.01 399.59 3.47 566.71 437.32 1 1.1766 0.1075 0.3528 0.15201 0.50983 0.75164 5.1297
01-Oct-1957 616.48 281.61 557.48 397.5 2.98 567.26 426.27 1 -1.2589 -0.375 -1.3979 -1.479 -0.29912 -0.23854 -8.014
01-Jan-1958 614.93 282.68 556.15 395.21 1.2 567.09 420.02 1 -1.2841 0.93338 -1.1283 -0.7527 -0.96303 -0.31126 -1.7628
01-Apr-1958 615.87 282.97 556.03 393.76 0.93 568.09 417.59 0 -0.30176 -0.40391 -0.55035 -0.37547 -0.50497 -0.11691 -2.2427
01-Jul-1958 618.76 283.57 558.99 394.95 1.76 569.81 427.67 0 1.872 0.4554 2.3388 1.7826 0.87564 0.89695 8.3152
01-Oct-1958 621.54 284.04 560.84 396.43 2.42 571.11 438.2 0 0.74477 0.054362 0.52207 0.66957 0.26535 -0.18234 4.4602
01-Jan-1959 623.66 284.31 563.55 398.35 2.8 573.62 442.12 0 0.52785 -0.063984 1.0562 1.1008 0.01065 0.93709 1.1838
01-Apr-1959 626.19 284.46 565.91 400.24 3.39 575.54 449.31 0 0.40825 -0.21958 0.44272 0.5194 -0.12278 0.36387 0.45836
logL
logL = -1.4656e+03
Tbl is a 238-by-15 timetable of in-sample data in DTT and inferred innovations (variable names appended with _Residuals).
Plot the residuals on separate plots. Synchronize the residuals with the dates by removing the first Mdl.P dates.
idx = endsWith(Tbl.Properties.VariableNames,"_Residuals"); resnames = Tbl.Properties.VariableNames(idx); titles = "Residuals: " + EstMdl.SeriesNames; figure tiledlayout(2,2) for j = 1:4 nexttile plot(Tbl.Time,Tbl{:,resnames(j)}) hold on yline(0,"r--") hold off title(titles(j)) end

figure tiledlayout(2,2) for j = 5:7 nexttile plot(Tbl.Time,Tbl{:,resnames(j)}) hold on yline(0,"r--") hold off title(titles(j)) end
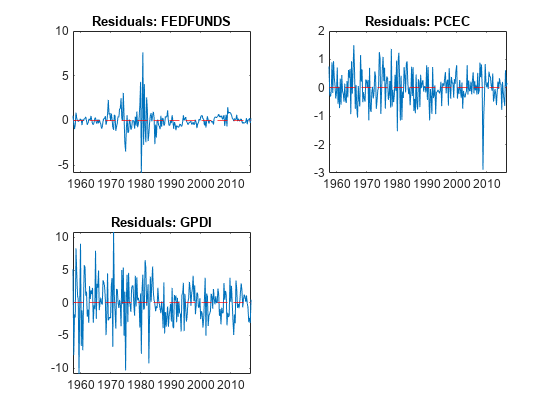
The residuals corresponding to the federal funds rate exhibit heteroscedasticity.
Input Arguments
Response data, specified as a
numobs-by-numseries numeric matrix or a
numobs-by-numseries-by-numpaths
numeric array.
numobs is the sample size. numseries is the
number of response series (Mdl.NumSeries).
numpaths is the number of response paths.
Rows correspond to observations, and the last row contains the latest observation.
Y represents the continuation of the presample response series in
Y0.
Columns must correspond to the response variable names in
Mdl.SeriesNames.
Pages correspond to separate, independent numseries-dimensional
paths. Among all pages, responses in a particular row occur at the same time.
Data Types: double
Since R2022b
Time series data containing observed response variables
yt and, optionally, predictor
variables xt for a model with a regression
component, specified as a table or timetable with numvars variables
and numobs rows.
Each selected response variable is a
numobs-by-numpaths numeric matrix, and each
selected predictor variable is a numeric vector. Each row is an observation, and
measurements in each row occur simultaneously. You can optionally specify
numseries response variables by using the
ResponseVariables name-value argument, and you can specify
numpreds predictor variables by using the
PredictorVariables name-value argument.
Paths (columns) within a particular response variable are independent, but path
jjnumpaths.
If Tbl1 is a timetable, it must represent a sample with a regular
datetime time step (see isregular), and the datetime vector
Tbl1.Time must be ascending or descending.
If Tbl1 is a table, the last row contains the latest
observation.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: infer(Mdl,Y,Y0=PS,X=Exo) computes the residuals of the
VEC(p – 1) model Mdl at the matrix of
response data Y, and specifies the matrix of presample response
data PS and the matrix of exogenous predictor data
Exo.
Since R2022b
Variables to select from Tbl1 to treat as response variables
yt, specified as one of the following
data types:
String vector or cell vector of character vectors containing
numseriesvariable names inTbl1.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromTbl1.Properties.VariableNamesA length
numvarslogical vector, whereResponseVariables(selects variablej) = truejTbl1.Properties.VariableNames, andsum(ResponseVariables)isnumseries
The selected variables must be numeric vectors (single path) or matrices (columns
represent multiple independent paths) of the same width, and cannot contain missing
values (NaN).
If the number of variables in Tbl1 matches
Mdl.NumSeries, the default specifies all variables in
Tbl1. If the number of variables in Tbl1
exceeds Mdl.NumSeries, the default matches variables in
Tbl1 to names in Mdl.SeriesNames.
Example: ResponseVariables=["GDP" "CPI"]
Example: ResponseVariables=[true false true false] or
ResponseVariable=[1 3] selects the first and third table
variables as the response variables.
Data Types: double | logical | char | cell | string
Presample responses that provide initial values for the model
Mdl, specified as a
numpreobs-by-numseries numeric matrix or a
numpreobs-by-numseries-by-numprepaths
numeric array. Use Y0 only when you supply a numeric array of
response data Y.
numpreobs is the number of presample observations.
numprepaths is the number of presample response paths.
Each row is a presample observation, and measurements in each row, among all pages,
occur simultaneously. The last row contains the latest presample observation.
Y0 must have at least Mdl.P rows. If you
supply more rows than necessary, infer uses the latest
Mdl.P observations only.
Each column corresponds to the response series associated with the respective response
series in Y.
Pages correspond to separate, independent paths.
If
Y0is a matrix,inferapplies it to each path (page) inY. Therefore, all paths inYderive from common initial conditions.Otherwise,
inferappliesY0(:,:,toj)Y(:,:,.j)Y0must have at leastnumpathspages, andinferuses only the firstnumpathspages.
By default, infer uses the first Mdl.P
observations, for example, Y(1:Mdl.P,:), as a presample. This action
reduces the effective sample size.
Data Types: double
Since R2022b
Presample data that provides initial values for the model Mdl,
specified as a table or timetable, the same type as Tbl1, with
numprevars variables and numpreobs
rows.
Each row is a presample observation, and measurements in each row, among all paths,
occur simultaneously. numpreobs must be at least
Mdl.P. If you supply more rows than necessary,
infer uses the latest Mdl.P
observations only.
Each variable is a numpreobs-by-numprepaths
numeric matrix. Variables correspond to the response series associated with the
respective response variable in Tbl1. To control presample variable
selection, see the optional PresampleResponseVariables name-value
argument.
For each variable, columns are separate, independent paths.
If variables are vectors,
inferapplies them to each path inTbl1to produce the corresponding residuals inTbl2. Therefore, all response paths derive from common initial conditions.Otherwise, for each variable
ResponseKjinferappliesPresample.to produceResponseK(:,j)Tbl2.. Variables must have at leastResponseK(:,j)numpathscolumns, andinferuses only the firstnumpathscolumns.
If Presample is a timetable, all the following conditions must be true:
Presamplemust represent a sample with a regular datetime time step (seeisregular).The inputs
Tbl1andPresamplemust be consistent in time such thatPresampleimmediately precedesTbl1with respect to the sampling frequency and order.The datetime vector of sample timestamps
Presample.Timemust be ascending or descending.
If Presample is a table, the last row contains the latest
presample observation.
By default, infer uses the first or earliest
Mdl.P observations in Tbl1 as a presample,
and then it fits the model to the remaining numobs – Mdl.P
observations. This action reduces the effective sample size.
Since R2022b
Variables to select from Presample to use
for presample data, specified as one of the
following data types:
String vector or cell vector of character vectors containing
numseriesvariable names inPresample.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromPresample.Properties.VariableNamesA length
numvarslogical vector, wherePresampleResponseVariables(selects variablej) = truejPresample.Properties.VariableNames, andsum(PresampleResponseVariables)isnumseries
The selected variables must be numeric vectors (single path)
or matrices (columns represent multiple independent
paths) of the same width, and cannot contain missing
values (NaN).
PresampleResponseNames does not need to
contain the same names as in
Tbl1;
infer uses the data in
selected variable
PresampleResponseVariables(
as a presample for the response variable
corresponding to
j)ResponseVariables(.j)
The default specifies the same response variables as those
selected from Tbl1 (see
ResponseVariables).
Example: PresampleResponseVariables=["GDP"
"CPI"]
Example: PresampleResponseVariables=[true false true
false] or
PresampleResponseVariable=[1 3]
selects the first and third table variables for
presample data.
Data Types: double | logical | char | cell | string
Predictor data xt for the regression
component in the model, specified as a numeric matrix containing
numpreds columns. Use X only when you supply a
numeric array of response data Y.
numpreds is the number of predictor variables
(size(Mdl.Beta,2)).
Each row corresponds to an observation, and measurements in each row occur
simultaneously. The last row contains the latest observation. X must
have at least as many observations as Y. If you supply more rows
than necessary, infer uses only the latest observations.
infer does not use the regression component in the
presample period.
If you specify a numeric array for a presample by using
Y0,Xmust have at leastnumobsrows (seeY).Otherwise,
Xmust have at leastnumobs–Mdl.Pobservations to account for the default presample removal fromY.
Each column is an individual predictor variable. All predictor variables are present in the regression component of each response equation.
infer applies X to each path (page) in
Y; that is, X represents one path of
observed predictors.
By default, infer excludes the regression component,
regardless of its presence in Mdl.
Data Types: double
Since R2022b
Variables to select from Tbl1 to treat as exogenous predictor variables
xt, specified as one of the following data types:
String vector or cell vector of character vectors containing
numpredsvariable names inTbl1.Properties.VariableNamesA length
numpredsvector of unique indices (integers) of variables to select fromTbl1.Properties.VariableNamesA length
numvarslogical vector, wherePredictorVariables(selects variablej) = truejTbl1.Properties.VariableNames, andsum(PredictorVariables)isnumpreds
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
By default, infer excludes the regression component, regardless
of its presence in Mdl.
Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]
Example: PredictorVariables=[true false true false] or
PredictorVariable=[1 3] selects the first and third table variables to
supply the predictor data.
Data Types: double | logical | char | cell | string
Note
NaNvalues inY,Y0, andXindicate missing values.inferremoves missing values from the data by list-wise deletion.If
Yis a 3-D array, theninferhorizontally concatenates the pages ofYto form anumobs-by-(numpaths*numseries + numpreds)matrix.If a regression component is present, then
inferhorizontally concatenatesXtoYto form anumobs-by-numpaths*numseries + 1matrix.inferassumes that the last rows of each series occur at the same time.inferremoves any row that contains at least oneNaNfrom the concatenated data.inferapplies steps 1 and 3 to the presample paths inY0.
This process ensures that the inferred output innovations of each path are the same size and are based on the same observation times. In the case of missing observations, the results obtained from multiple paths of
Ycan differ from the results obtained from each path individually.This type of data reduction reduces the effective sample size.
inferissues an error when any table or timetable input contains missing values.
Output Arguments
Inferred multivariate innovations series, returned as either a numeric matrix, or as a
numeric array that contains columns and pages corresponding to Y.
infer returns E only when you supply a
matrix of response data Y.
If you specify
Y0, thenEhasnumobsrows (seeY).Otherwise,
Ehasnumobs–Mdl.Prows to account for the presample removal.
Since R2022b
Inferred multivariate innovations series and other variables, returned as a table or
timetable, the same data type as Tbl1.
infer returns Tbl2 only when you
supply the input Tbl1.
Tbl2 contains the inferred innovation paths E
from evaluating the model Mdl at the paths of selected response
variables Y, and it contains all variables in
Tbl1. infer names the innovation
variable corresponding to variable
ResponseJTbl1
ResponseJ_ResidualsTbl1 is
GDP, Tbl2 contains a variable for the
residuals in the response equation of GDP with the name
GDP_Residuals.
If you specify presample response data, Tbl2 and
Tbl1 have the same number of rows, and their rows correspond.
Otherwise, because infer removes initial observations from
Tbl1 for the required presample by default,
Tbl2 has numobs – Mdl.P rows to account for
that removal.
If Tbl1 is a timetable, Tbl1 and
Tbl2 have the same row order, either ascending or
descending.
Loglikelihood objective function value, returned as a numeric scalar or a
numpaths-element numeric vector.
logL( corresponds to the
response path in j)Y(:,:, or the path
(column) j)jTbl1.
Algorithms
Suppose Y, Y0, and X are the
response, presample response, and predictor data specified by the numeric data inputs in
Y, Y0, and X, or the
selected variables from the input tables or timetables Tbl1 and
Presample.
inferinfers innovations by evaluating the VEC modelMdl, specificallyinferuses this process to determine the time origin t0 of models that include linear time trends.If you do not specify
Y0, then t0 = 0.Otherwise,
infersets t0 tosize(Y0,1)–Mdl.P. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numobs, wherenumobsis the effective sample size (size(Y,1)afterinferremoves missing values). This convention is consistent with the default behavior of model estimation in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughinferexplicitly uses the firstMdl.Ppresample responses inY0to initialize the model, the total number of observations inY0andY(excluding missing values) determines t0.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.
Version History
Introduced in R2017bIn addition to accepting input data in numeric arrays,
infer accepts input data in tables and timetables. infer chooses default series on which to operate, but you can use the following name-value arguments to select variables.
ResponseVariablesspecifies the response series names in the input data from which residuals are inferred.PredictorVariablesspecifies the predictor series names in the input data for a model regression component.Presamplespecifies the input table or timetable of presample response data.PresampleResponseVariablesspecifies the response series names fromPresample.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)