Detect Overflows
This example shows how to detect overflows using the Fixed-Point Converter app. At the numerical testing stage in the conversion process, you choose to simulate the fixed-point code using scaled doubles. The app then reports which expressions in the generated code produce values that overflow the fixed-point data type.
Prerequisites
This example requires the following products:
MATLAB®
Fixed-Point Designer™
C compiler
See Supported Compilers.
You can use
mex -setupto change the default compiler. See Change Default Compiler.
Create a New Folder and Copy Relevant Files
In a local, writable folder, create a function
overflow.m.function y = overflow(b,x,reset) if nargin<3, reset = true; end persistent z p if isempty(z) || reset p = 0; z = zeros(size(b)); end [y,z,p] = fir_filter(b,x,z,p); end function [y,z,p] = fir_filter(b,x,z,p) y = zeros(size(x)); nx = length(x); nb = length(b); for n = 1:nx p=p+1; if p>nb, p=1; end z(p) = x(n); acc = 0; k = p; for j=1:nb acc = acc + b(j)*z(k); k=k-1; if k<1, k=nb; end end y(n) = acc; end end
Create a test file,
overflow_test.m, to exercise theoverflowalgorithm. You use this test file to define input types forb,x, andreset, and, later, to verify the fixed-point version of the algorithm.function overflow_test % The filter coefficients were computed % using the FIR1 function from % Signal Processing Toolbox. % b = fir1(11,0.25); b = [-0.004465461051254 -0.004324228005260 +0.012676739550326 +0.074351188907780 +0.172173206073645 +0.249588554524763 +0.249588554524763 +0.172173206073645 +0.074351188907780 +0.012676739550326 -0.004324228005260 -0.004465461051254]'; % Input signal nx = 256; t = linspace(0,10*pi,nx)'; % Impulse x_impulse = zeros(nx,1); x_impulse(1) = 1; % Max Gain % The maximum gain of a filter will occur when the % inputs line up with the signs of the filter's % impulse response. x_max_gain = sign(b)'; x_max_gain = repmat(x_max_gain,ceil(nx/length(b)),1); x_max_gain = x_max_gain(1:nx); % Sums of sines f0=0.1; f1=2; x_sines = sin(2*pi*t*f0) + 0.1*sin(2*pi*t*f1); % Chirp f_chirp = 1/16; % Target frequency x_chirp = sin(pi*f_chirp*t.^2); % Linear chirp x = [x_impulse,x_max_gain,x_sines,x_chirp]; titles = {'Impulse','Max gain','Sum of sines','Chirp'}; y = zeros(size(x)); for i=1:size(x,2) reset = true; y(:,i) = overflow(b,x(:,i),reset); end test_plot(1,titles,t,x,y) end function test_plot(fig,titles,t,x,y1) figure(fig) clf sub_plot = 1; font_size = 10; for i=1:size(x,2) subplot(4,1,sub_plot) sub_plot = sub_plot+1; plot(t,x(:,i),'c',t,y1(:,i),'k') axis('tight') xlabel('t','FontSize',font_size); title(titles{i},'FontSize',font_size); ax = gca; ax.FontSize = 10; end figure(gcf) end
It is a best practice is to create a separate test script to do pre- and post-processing, such as:
Loading inputs.
Setting up input values.
Outputting test results.
For more information, see Create a Test File.
| Type | Name | Description |
|---|---|---|
| Function code | overflow.m | Entry-point MATLAB function |
| Test file | overflow_test.m | MATLAB script that tests
overflow.m |
Open the Fixed-Point Converter App
Navigate to the work folder that contains the file for this example.
On the MATLAB Toolstrip Apps tab, under Code Generation, click the app icon.

Select Source Files
To add the entry-point function
overflowto the project, browse to the fileoverflow.m, and then click Open. By default, the app saves information and settings for this project in the current folder in a file namedoverflow.prj.Click Next to go to the Define Input Types step.
The app screens
overflow.mfor code violations and fixed-point conversion readiness issues. The app does not find issues inoverflow.m.
Define Input Types
On the Define Input Types page, to add
overflow_testas a test file, browse tooverflow_test.m, and then click Open.Click Autodefine Input Types.
The test file runs. The app determines from the test file that the input type of
bisdouble(1x12),xisdouble(256x1), andresetislogical(1x1).
Click Next to go to the Convert to Fixed Point step.
Convert to Fixed Point
The app generates an instrumented MEX function for your entry-point MATLAB function. The app displays compiled information — type, size, and complexity — for variables in your code. For more information, see View and Modify Variable Information.

On the Function Replacements tab the app displays functions that are not supported for fixed-point conversion. See Running a Simulation.
To view the fimath settings, click the Settings arrow
 . Set the fimath Product
mode and Sum mode to
. Set the fimath Product
mode and Sum mode to
KeepLSB. These settings model the behavior of integer operations in the C language.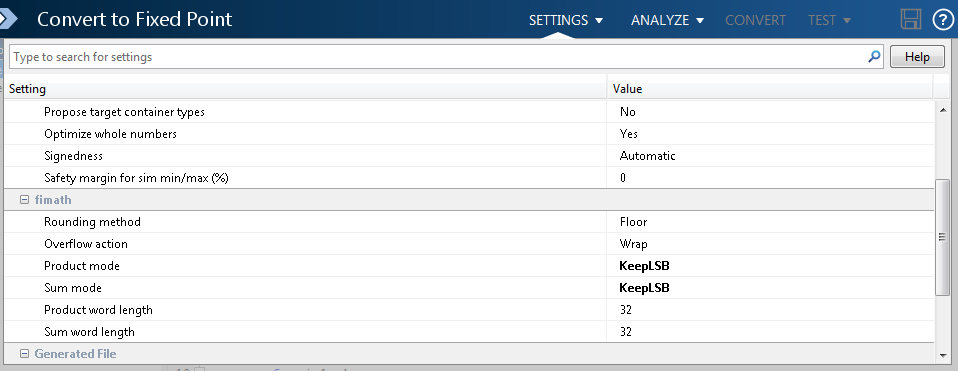
Click Analyze.
The test file,
overflow_test, runs. The app displays simulation minimum and maximum ranges on the Variables tab. Using the simulation range data, the software proposes fixed-point types for each variable based on the default type proposal settings, and displays them in the Proposed Type column.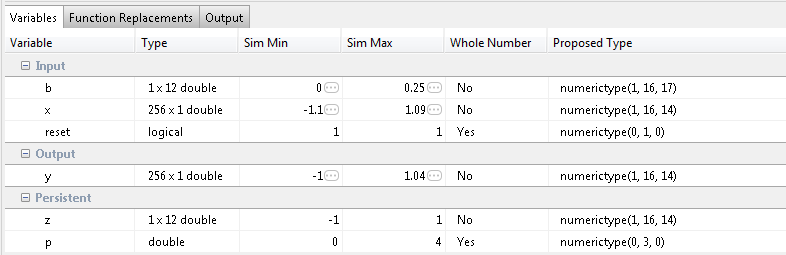
To convert the floating-point algorithm to fixed point, click Convert.
The software validates the proposed types and generates a fixed-point version of the entry-point function.
If errors and warnings occur during validation, the app displays them on the Output tab. See Validating Types.
Test Numerics and Check for Overflows
Click the Test arrow
 . Verify that the test file is
. Verify that the test file is
overflow_test.m. Select Use scaled doubles to detect overflows, and then click Test.The app runs the test file that you used to define input types to test the fixed-point MATLAB code. Because you selected to detect overflows, it also runs the simulation using scaled double versions of the proposed fixed-point types. Scaled doubles store their data in double-precision floating-point, so they carry out arithmetic in full range. Because they retain their fixed-point settings, they can report when a computation goes out of the range of the fixed-point type.
The simulation runs. The app detects an overflow. The app reports the overflow on the Overflow tab. To highlight the expression that overflowed, click the overflow.

Determine whether it was the sum or the multiplication that overflowed.
In the fimath settings, set Product mode to
FullPrecision, and then repeat the conversion and test the fixed-point code again.The overflow still occurs, indicating that it is the addition in the expression that is overflowing.
