Pareto Front for Multiobjective Optimization, Problem-Based
This example shows how to solve a multiobjective optimization problem using optimization variables, and how to plot the solution.
Problem Formulation
The problem has a two-dimensional optimization variable and two objective functions. Create the optimization variable x as a row vector, the orientation expected by multiobjective solvers. Set bounds specifying that the components of x range from –50 through 50.
x = optimvar("x",1,2,LowerBound=-50,UpperBound=50);Create the two-component objective function. Include the objective function in an optimization problem.
fun(1) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 - 9*x(1)^2;
fun(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 + 3*x(2)^3;
prob = optimproblem("Objective",fun);Review the problem.
show(prob)
OptimizationProblem :
Solve for:
x
minimize :
((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) - (9 .* x(1).^2))
((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) + (3 .* x(2).^3))
variable bounds:
-50 <= x(1) <= 50
-50 <= x(2) <= 50
Solve and Plot Solution
Call solve to solve the problem.
rng default % For reproducibility sol = solve(prob)
Solving problem using gamultiobj. gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
sol =
1×18 OptimizationValues vector with properties:
Variables properties:
x: [2×18 double]
Objective properties:
Objective: [2×18 double]
Plot the resulting Pareto front.
paretoplot(sol)
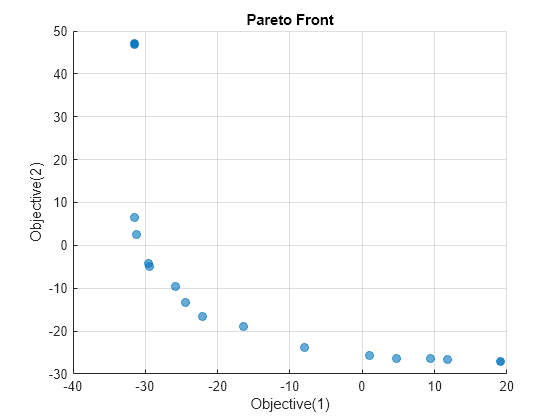
Solve the problem again using the paretosearch solver.
sol2 = solve(prob,Solver="paretosearch");Solving problem using paretosearch. Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
paretoplot(sol2)

Using default options, the paretosearch solver obtains a denser set of solution points than gamultiobj. However, gamultiobj obtains a wider range of values.
Start from Single-Objective Solutions
To attempt to achieve a better spread of solutions, find the single-objective solutions starting from x = [1 1].
x0.x = [1 1];
prob1 = optimproblem("Objective",fun(1));
solp1 = solve(prob1,x0);Solving problem using fmincon. Local minimum possible. Constraints satisfied. fmincon stopped because the size of the current step is less than the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
prob2 = optimproblem("Objective",fun(2));
solp2 = solve(prob2,x0);Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
Prepare the single-objective solutions as an initial point for solve. Each point must be passed as a column vector to the optimvalues function.
start = optimvalues(prob,"x",[solp1.x' solp2.x']);Solve the multiobjective problem with paretosearch starting from the start points.
sol3 = solve(prob,start,Solver="paretosearch");Solving problem using paretosearch. Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
paretoplot(sol3)
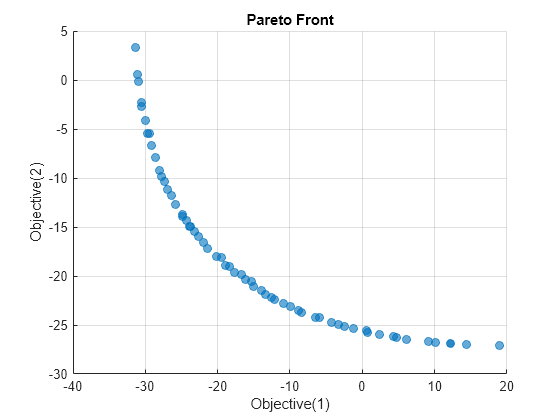
This time, paretosearch finds a larger range of the objective functions, going almost to 10 in Objective 2 and almost to 20 in Objective 1. This range is similar to the gamultiobj range, except for the anomalous solution point near Objective 1 = –31, Objective 2 = 48.
See Also
gamultiobj | paretosearch | solve | paretoplot