Condenser Evaporator (2P-MA)

Heat exchanger between moist air and two-phase fluid networks

• 

Libraries:
Simscape / Fluids / Heat Exchangers / Two-Phase Fluid - Moist Air

Description

The Condenser Evaporator (2P-MA) block models a heat exchanger with one moist air network, which flows between ports A2 and B2, and one two-phase fluid network, which flows between ports A1 and B1. The heat exchanger can act as a condenser or as an evaporator. The fluid streams can be aligned in parallel, counter, or cross-flow configurations.

Example Heat Exchanger for Refrigeration Applications

You can model the moist air side as flow within tubes, flow around the two-phase fluid tubing, or by an empirical, generic parameterization. The moist air side comprises air, trace gas, and water vapor that may condense throughout the heat exchange cycle. The block model accounts for energy transfer from the air to the liquid water condensation layer. This liquid layer does not collect on the heat transfer surface and is assumed to be completely removed from the downstream moist air flow. The humidity condensation rate is returned as a physical signal at port W.

The block uses the Effectiveness-NTU (E-NTU) method to model heat transfer through the shared wall. Fouling on the exchanger walls, which increases thermal resistance and reduces the heat exchange between the two fluids, is also modeled. You can also optionally model fins on both the moist air and two-phase fluid sides. Pressure loss due to viscous friction on both sides of the exchanger can be modeled analytically or by generic parameterization, which you can use to tune to your own data.

You can model the two-phase fluid side as flow within a tube or a set of tubes. The two-phase fluid tubes use a boundary-following model to track the sub-cooled liquid (L), vapor-liquid mixture (M), and super-heated vapor (V) in three zones. The relative amount of space a zone occupies in the system is called a zone length fraction within the system.

Zone Length Fractions in the Two-Phase Fluid Piping

The sum of the zone length fractions in the two-phase fluid tubing equals 1. Port Z returns the zone length fractions as a vector of physical signals for each of the three phases: [L, M, V].

Heat Exchanger Configuration

The heat exchanger effectiveness is based on the selected heat exchanger configuration, the fluid properties in each phase, the tube geometry and flow configuration on each side of the exchanger, and the usage and size of fins.

Flow Arrangement

The Flow arrangement parameter assigns the relative flow paths between the two sides:

• Parallel flow indicates the fluids are moving in the same direction.

• Counter flow indicates the fluids are moving in parallel, but opposite directions.

• Cross flow indicates the fluids are moving perpendicular to each other.

Thermal Mixing

When Flow arrangement is set to Cross flow, use the Cross flow arrangement parameter to indicate whether the two-phase fluid or moist air flows are separated into multiple paths by baffles or walls. Without these separations, the flow can mix freely and is considered mixed. Both fluids, one fluid, or neither fluid can be mixed in the cross-flow arrangement. Mixing homogenizes the fluid temperature along the direction of flow of the second fluid, and varies perpendicular to the second fluid flow.

Unmixed flows vary in temperature both along and perpendicular to the flow path of the second fluid.

Sample Cross-Flow Configurations

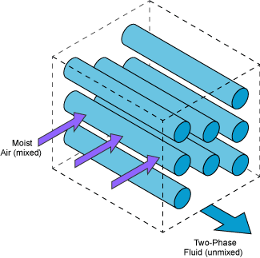
Note that the flow direction during simulation does not impact the selected flow arrangement setting. The ports on the block do not reflect the physical positions of the ports in the physical heat exchange system.

All flow arrangements are single-pass, which means that the fluids do not make multiple turns in the exchanger for additional points of heat transfer. To model a multi-pass heat exchanger, you can arrange multiple Condenser Evaporator (2P-MA) blocks in series or in parallel.

For example, to achieve a two-pass configuration on the two-phase fluid side and a single-pass configuration on the moist air side, you can connect the two-phase fluid sides in series and the moist air sides to the same input in parallel (such as two Mass Flow Rate Source blocks with half of the total mass flow rate), as shown below.

Flow Geometry

The Flow geometry parameter sets the moist air flow arrangement as either inside a tube or set of tubes, or perpendicular to a tube bank. You can also specify an empirical, generic configuration. The two-phase fluid always flows inside a tube or set of tubes.

When Flow geometry is set to Flow perpendicular to bank of circular tubes, use the Tube bank grid arrangement parameter to define the two-phase fluid tube bank alignment as either Inline or Staggered. The red, downward-pointing arrow indicates the direction of moist air flow. Also indicated in the Inline figure are the Number of tube rows along flow direction and the Number of tube segments in each tube row parameters. Here, flow direction refers to the moist air flow, and tube refers to the two-phase fluid tubing. The Length of each tube segment in a tube row parameter is indicated in the Staggered figure.

Fins

The heat exchanger configuration does not have fins when the Total fin surface area parameter is 0 m^2. Fins introduce additional surface area for heat transfer. Each fluid side has a separate fin area and parameters that describe the fins in that fluid. For example, when the two-phase fluid flows inside the tubes and the moist air flows outside of the tubes, the Total fin surface area and Fin efficiency parameters in the Two-Phase Fluid 1 section describe the fins protruding into the tube. The Total fin surface area and Fin efficiency parameters in the Moist Air 2 section describe the fins outside of the tubes.

Effectiveness-NTU Heat Transfer

The heat transfer rate is calculated for each fluid phase. In accordance with the three fluid zones that occur on the two-phase fluid side of the heat exchanger, the heat transfer rate is calculated in three sections.

The convective heat transfer in a zone is

$$Q_{zone}=ϵC_{\text{Min}}(T_{\text{In,2P}}-T_{\text{In,MA}}),$$

where:

• C_Min is the lesser of the heat capacity rates of the two fluids in that zone. The heat capacity rate is the product of the fluid specific heat, c_p, and the fluid mass flow rate. C_Min is always positive.

• T_In,2P is the zone inlet temperature of the two-phase fluid.

• T_In,MA is the zone inlet temperature of the moist air.

• ε is the heat exchanger effectiveness.

Effectiveness is a function of the heat capacity rate and the number of transfer units, NTU, and also varies based on the heat exchanger flow arrangement, which is discussed in more detail in Effectiveness by Flow Arrangement. The NTU is calculated as:

$$NTU=\frac{z}{C_{\text{Min}}R},$$

where:

• z is the individual zone length fraction.

• R is the total thermal resistance between the two flows, due to convection, conduction, and any fouling on the tube walls.

  $$R=\frac{1}{U_{\text{2P}}{A}_{\text{Th,2P}}}+\frac{F_{\text{2P}}}{A_{\text{Th,2P}}}+R_{\text{W}}+\frac{F_{\text{MA}}}{A_{\text{Th,MA}}}+\frac{1}{U_{\text{MA}}{A}_{\text{Th,MA}}},$$

  where:

  • U is the convective heat transfer coefficient of the respective fluid. This coefficient is discussed in more detail in Two-Phase Fluid Correlations and Moist Air Correlations.

  • F is the value of the Fouling factor parameter on the two-phase fluid or moist air side, respectively.

  • R_W is the value of the Thermal resistance through heat transfer surface parameter.

  • A_Th is the heat transfer surface area of the respective side of the exchanger. A_Th is the sum of the wall surface area, A_W, and the Total fin surface area, A_F:

    $$A_{\text{Th}}=A_{\text{W}}+{\eta }_{\text{F}}{A}_{\text{F}},$$

    where η_F is the Fin efficiency.

The total convective heat transfer rate between the fluids is the sum of the heat transferred in the three zones by the subcooled liquid (Q_L), liquid-vapor mixture (Q_M), and superheated vapor (Q_V):

$$Q={\displaystyle \sum Q_{\text{Z}}}=Q_{\text{L}}+Q_{\text{M}}+Q_{\text{V}}.$$

Effectiveness by Flow Arrangement

The heat exchanger effectiveness varies according to its flow configuration and the mixing in each fluid. Below are the formulations for effectiveness calculated in the liquid and vapor zones for each configuration. The effectiveness is $$\epsilon =1-\exp (-NTU)$$ for all configurations in the mixture zone.

• When Flow arrangement is set to Parallel flow:

  $$ϵ=\frac{1-\text{exp}[-NTU(1+C_{\text{R}})]}{1+C_{\text{R}}}$$

• When Flow arrangement is set to Counter flow:

  $$ϵ=\frac{1-\text{exp}[-NTU(1-C_{\text{R}})]}{1-C_{\text{R}}\text{exp}[-NTU(1-C_{\text{R}})]}$$

• When Flow arrangement is set to Cross flow and Cross flow arrangement is set to Both fluids unmixed:

  $$ϵ=1-\text{exp}\left\{\frac{NT{U}^{\text{0}\text{.22}}}{C_{\text{R}}}\left[\text{exp}\left(-C_{\text{R}}NT{U}^{\text{0}\text{.78}}\right)-1\right]\right\}$$

• When Flow arrangement is set to Cross flow and Cross flow arrangement is set to Both fluids mixed:

  $$ϵ={\left[\frac{1}{1-\text{exp}\left(-NTU\right)}+\frac{C_{\text{R}}}{1-\text{exp}\left(-C_{\text{R}}NTU\right)}-\frac{1}{NTU}\right]}^{-1}$$

When one fluid is mixed and the other unmixed, the equation for effectiveness depends on the relative heat capacity rates of the fluids. When Flow arrangement is set to Cross flow and Cross flow arrangement is set to either Two-Phase Fluid 1 mixed & Moist Air 2 unmixed or Two-Phase Fluid 1 unmixed & Moist Air 2 mixed:

• When the fluid with C_max is mixed and the fluid with C_min is unmixed:

  $$ϵ=\frac{1}{C_{\text{R}}}\left(1-\text{exp}\left\{-C_R\left\{1-\exp \left(-NTU\right)\right\}\right\}\right)$$

• When the fluid with C_min is mixed and the fluid with C_max is unmixed:

  $$ϵ=1-\text{exp}\left\{-\frac{1}{C_{\text{R}}}\left[1-\text{exp}\left(-C_{\text{R}}NTU\right)\right]\right\}$$

C_R denotes the ratio between the heat capacity rates of the two fluids:

$$C_{\text{R}}=\frac{C_{\text{Min}}}{C_{\text{Max}}}.$$

Conductive Heat Transfer

The conductive heat transfer in a zone is

$$Q_{cond}=\frac{T_{out,2P}-T_{out,MA}}{R_{cond}},$$

where:

• T_out,2P is the zone outlet temperature of the two-phase fluid.

• T_out,MA is the zone outlet temperature of the moist air.

• R_cond is the total conductive thermal resistance between the two flows,

  $$R_{cond}=\frac{D_h}{k_{\text{2P}}{A}_{\text{W,2P}}}+\frac{F_{\text{2P}}}{A_{\text{W,2P}}}+R_{\text{W}}+\frac{F_{\text{MA}}}{A_{\text{W,MA}}}+\frac{D_h}{k_{\text{MA}}{A}_{\text{W,MA}}},$$

  where:

  • A_W is the wall surface area.

  • k is the thermal conductivity of each fluid.

  • D_H is the hydraulic diameter.

The total heat transfer is the sum of the convective and conductive heat transfer. The conductive heat transfer is negligible compared to the convective heat transfer. When the flow rate is zero, the convective heat transfer is also zero. However, because heat transfer from convection and conduction operate independently of each other, there is still conductive heat transfer even when the convective heat transfer is zero.

Condensation

On the moist air side, a layer of condensation may form on the heat transfer surface. This liquid layer can influence the amount of heat transferred between the moist air and two-phase fluid. The equations for E-NTU heat transfer above are given for dry heat transfer. To correct for the influence of condensation, the E-NTU equations are additionally calculated with the wet parameters listed below. Whichever of the two calculated heat flow rates results in a larger amount of moist air side cooling is used in heat calculations [1][2]. To use this method, the Lewis number is assumed to be close to 1, which is true for moist air [1][2].

E-NTU Quantities Used for Heat Transfer Rate Calculations

	Dry calculation	Wet calculation
Moist air zone inlet temperature	Tin,MA	Tin,wb,MA
Heat capacity rate	$${\overline{\dot{m}}}_{MA}{\overline{c}}_{p,MA}$$	$${\overline{\dot{m}}}_{MA}{\overline{c}}_{eq,MA}$$
Heat transfer coefficient	UMA	$$U_{MA}\frac{{\overline{c}}_{eq,MA}}{{\overline{c}}_{p,MA}}$$

where:

• T_in,MA is the moist air zone inlet temperature.

• T_in,wb,MA is the moist air wet-bulb temperature associated with T_in,MA.

• $${\overline{\dot{m}}}_{MA}$$ is the dry air mass flow rate.

• $${\overline{c}}_{p,MA}$$ is the moist air heat capacity per unit mass of dry air.

• $${\overline{c}}_{eq,MA}$$ is the equivalent heat capacity. The equivalent heat capacity is the change in the moist air specific enthalpy (per unit of dry air), $${\overline{h}}_{MA}$$, with respect to temperature at saturated moist air conditions:

  $${\overline{c}}_{eq,MA}={\left(\frac{\partial {\overline{h}}_{MA}}{\partial T_{MA}}\right)}_s.$$

The mass flow rate of the condensed water vapor leaving the moist air mass flow depends on the relative humidity between the moist air inlet and the channel wall and the heat exchanger NTUs:

$${\dot{m}}_{cond}=-{\overline{\dot{m}}}_{MA}\left(W_{wall,MA}-W_{in,MA}\right)\left(1-e^{-NT{U}_{MA}}\right),$$

where:

• W_wall,MA is the humidity ratio at the heat transfer surface.

• W_in,MA is the humidity ratio at the moist air flow inlet.

• NTU_MA is the number of transfer units on the moist air side, calculated as:

  $$NT{U}_{MA}=\frac{U_{MA}\frac{{\overline{c}}_{eq,MA}}{{\overline{c}}_{p,MA}}{A}_{Th,MA}}{{\overline{\dot{m}}}_{MA}{\overline{c}}_{eq,MA}}.$$

The energy flow associated with water vapor condensation is based on the difference between the vapor specific enthalpy, h_{water, wall}, and the specific enthalpy of vaporization, h_fg, for water:

$${\varphi }_{Cond}={\dot{m}}_{cond}\left(h_{water,wall}-h_{fg}\right).$$

The condensate is assumed to not accumulate on the heat transfer surface, and does not influence geometric parameters such as tube diameter. The condensed water is assumed to be completely removed from the downstream moist air flow.

Two-Phase Fluid Correlations

Heat Transfer Coefficient

The convective heat transfer coefficient varies according to the fluid Nusselt number:

$$U=\frac{\text{Nu}k}{D_{\text{H}}},$$

where:

• Nu is the zone mean Nusselt number, which depends on the flow regime.

• k is the fluid phase thermal conductivity.

• D_H is tube hydraulic diameter.

For turbulent flows in the subcooled liquid or superheated vapor zones, the Nusselt number is calculated with the Gnielinski correlation:

$$\text{Nu}=\frac{\frac{f_D}{8}(\text{Re}-1000)\text{Pr}}{1+12.7\sqrt{\frac{f}{8}}({\text{Pr}}^{2/3}-1)},$$

where:

• Re is the fluid Reynolds number.

• Pr is the fluid Prandtl number.

For turbulent flows in the liquid-vapor mixture zone, the Nusselt number is calculated with the Cavallini-Zecchin correlation:

$$\text{Nu}=\frac{{\text{aRe}}_{\text{SL}}^b{\text{Pr}}_{\text{SL}}^c\left\{{\left[\left(\sqrt{\frac{{\rho }_{\text{SL}}}{{\rho }_{\text{SV}}}}-1\right)x_{\text{Out}}+1\right]}^{1+b}-{\left[\left(\sqrt{\frac{{\rho }_{\text{SL}}}{{\rho }_{\text{SV}}}}-1\right)x_{\text{In}}+1\right]}^{1+b}\right\}}{\left(1+b\right)\left(\sqrt{\frac{{\rho }_{\text{SL}}}{{\rho }_{\text{SV}}}}-1\right)(x_{\text{Out}}-x_{\text{In}})}.$$

where:

• Re_SL is the Reynolds number of the saturated liquid.

• Pr_SL is the Prandtl number of the saturated liquid.

• ρ_SL is the density of the saturated liquid.

• ρ_SV is the density of the saturated vapor.

• a= 0.05, b = 0.8, and c= 0.33.

For laminar flows, the Nusselt number is set by the Laminar flow Nusselt number parameter.

For transitional flows, the Nusselt number is a blend between the laminar and turbulent Nusselt numbers.

Empirical Nusselt Number Formulation

When the Heat transfer coefficient model parameter is Colburn equation, the block calculates the Nusselt number for the subcooled liquid and superheated vapor zones by using the empirical Colburn equation

$$\text{Nu}=a{\text{Re}}^b{\text{Pr}}^c,$$

where a, b, and c are values in the Coefficients [a, b, c] for a*Re^b*Pr^c in liquid zone and Coefficients [a, b, c] for a*Re^b*Pr^c in vapor zone parameters.

The block calculates the Nusselt number for liquid-vapor mixture zones by using the Cavallini-Zecchin equation with the variables in the Coefficients [a, b, c] for a*Re^b*Pr^c in mixture zone parameter.

Pressure Loss

The pressure loss due to viscous friction varies depending on flow regime and configuration. The pressure loss calculation uses the overall density, which is the total fluid mass divided by the total fluid volume. When the Pressure loss model parameter is Correlation for flow inside tubes, the pressure loss due to friction depends on the Darcy friction factor.

For turbulent flows, when the Reynolds number is above the Turbulent flow lower Reynolds number limit parameter, the block calculates the pressure loss due to friction in terms of a calculated Darcy friction factor. The pressure differential between port A1 and the internal node I1 is:

$$p_{\text{A1}}-p_{\text{I1}}=\frac{f_{\text{D,A}}{\dot{m}}_{\text{A1}}\left|{\dot{m}}_{\text{A1}}\right|}{2\rho D_{\text{H}}{A}_{\text{CS}}^2}\left(\frac{L+L_{\text{Add}}}{2}\right),$$

where:

• $$\dot{m}$$_A1 is the total flow rate through port A1.

• f_D,A is the Darcy friction factor according to the Haaland correlation. When the Local resistance specification parameter is Aggregate equivalent length,

  $$f_{\text{D,A1}}={\left\{-1.8{\text{log}}_{\text{10}}\left[\frac{6.9}{{\text{Re}}_{\text{A1}}}+{\left(\frac{{ϵ}_{\text{R}}}{3.7D_{\text{H}}}\right)}^{1.11}\right]\right\}}^{\text{-2}},$$

  where ε_R is the value of the Internal surface absolute roughness parameter. The friction factor is dependent on the Reynolds number, and the block calculates this value at both ports for each liquid.

• L is the value of the Total length of each tube parameter.

• L_Add is the value of the Aggregate equivalent length of local resistances parameter, which is the equivalent length of a tube that introduces the same amount of loss as the sum of the losses due to other local resistances in the tube.

• A_CS is the tube cross-sectional area.

The pressure differential between port B1 and internal node I1 is:

$$p_{\text{B1}}-p_{\text{I1}}=\frac{f_{\text{D,B}}{\dot{m}}_{\text{B1}}\left|{\dot{m}}_{\text{B1}}\right|}{2\rho D_{\text{H}}{A}_{\text{CS}}^2}\left(\frac{L+L_{\text{Add}}}{2}\right),$$

where $$\dot{m}$$_B1 is the total flow rate through port B1.

When the Local resistance specification parameter is Aggregate equivalent length, the Darcy friction factor at port B1 is:

$$f_{\text{D,B1}}={\left\{-1.8{\text{log}}_{\text{10}}\left[\frac{6.9}{{\text{Re}}_{\text{B1}}}+{\left(\frac{{ϵ}_{\text{R}}}{3.7D_{\text{H}}}\right)}^{1.11}\right]\right\}}^{\text{-2}}.$$

When the Local resistance specification parameter is Local loss coefficient, the Darcy friction factors at ports A1 and B1 are

$$\begin{array}{l}{f}_{\text{D,A1}}={\left\{-1.8{\text{log}}_{\text{10}}\left[\frac{6.9}{{\text{Re}}_{A1}}+{\left(\frac{{ϵ}_{\text{R}}}{3.7D_{\text{H}}}\right)}^{1.11}\right]\right\}}^{\text{-2}}+C_{localloss}\left(\frac{D_H}{L}\right)\\ f_{\text{D,B1}}={\left\{-1.8{\text{log}}_{\text{10}}\left[\frac{6.9}{{\text{Re}}_{B1}}+{\left(\frac{{ϵ}_{\text{R}}}{3.7D_{\text{H}}}\right)}^{1.11}\right]\right\}}^{\text{-2}}+C_{localloss}\left(\frac{D_H}{L}\right)\end{array}$$

where C_localloss is the value of the Total local loss coefficient parameter.

For laminar flows, when the Reynolds number is below the Laminar flow upper Reynolds number limit parameter, the block calculates the pressure loss due to friction in terms of the Laminar friction constant for Darcy friction factor parameter, λ. λ is a user-defined parameter when Tube cross-section is Generic. Otherwise, the block calculates the value internally. The pressure differential between port A1 and internal node I1 is:

$$p_{\text{A1}}-p_{\text{I1}}=\frac{\lambda \mu {\dot{m}}_{\text{A1}}}{2\rho D_{\text{H}}^2{A}_{CS}}\left(\frac{L+L_{\text{Add}}}{2}\right),$$

where μ is the fluid dynamic viscosity. The pressure differential between port B1 and internal node I1 is:

$$p_{\text{B1}}-p_{\text{I1}}=\frac{\lambda \mu {\dot{m}}_{\text{B1}}}{2\rho D_{\text{H}}^2{A}_{CS}}\left(\frac{L+L_{\text{Add}}}{2}\right).$$

For transitional flows, the pressure differential due to viscous friction is a smoothed blend between the values for laminar and turbulent pressure losses.

Empirical Pressure Loss Formulation

When Pressure loss model is set to Pressure loss coefficient, the pressure losses due to viscous friction are calculated with an empirical pressure loss coefficient, ξ.

The pressure differential between port A1 and internal node I1 is:

$$p_{\text{A1}}-p_{\text{I1}}=\frac{1}{2}\xi \frac{{\dot{m}}_{\text{A1}}\left|{\dot{m}}_{\text{A1}}\right|}{2\rho A_{\text{CS}}^2}.$$

The pressure differential between port B1 and internal node I1 is:

$$p_{\text{B1}}-p_{\text{I1}}=\frac{1}{2}\xi \frac{{\dot{m}}_{\text{B1}}\left|{\dot{m}}_{\text{B1}}\right|}{2\rho A_{\text{CS}}^2}.$$

Moist Air Correlations

Heat Transfer Coefficient for Flows Inside One or More Tubes

When the moist air Flow geometry is set to Flow inside one or more tubes, the Nusselt number is calculated according to the Gnielinski correlation in the same manner as two-phase supercooled liquid or superheated vapor. See Heat Transfer Coefficient for more information.

Heat Transfer Coefficient for Flows Across a Tube Bank

When the moist air Flow geometry is set to Flow perpendicular to bank of circular tubes, the Nusselt number is calculated based on the Hagen number, Hg, and depends on the Tube bank grid arrangement setting:

$$\text{Nu}=\{\begin{array}{cc}0.404L{q}^{\text{1/3}}{\left(\frac{\text{Re}+1}{\text{Re}+1000}\right)}^{0.1},& Inline\\ 0.404L{q}^{1/3},& Staggered\end{array}$$

where:

$$Lq=\{\begin{array}{cc}1.18\text{Pr}\left(\frac{4l_{\text{T}}/\pi -D}{l_{\text{L}}}\right)\text{Hg}(\text{Re}),& Inline\\ 0.92\text{Pr}\left(\frac{4l_{\text{T}}/\pi -D}{l_{\text{D}}}\right)\text{Hg}(\text{Re}),& Staggeredwith{l}_L\ge D\\ 0.92\text{Pr}\left(\frac{4l_{\text{T}}{l}_{\text{L}}/\pi -D^2}{l_{\text{L}}{l}_{\text{D}}}\right)\text{Hg}(\text{Re}),& Staggeredwith{l}_L<D\end{array}$$

• D is the Tube outer diameter.

• l_L is the Longitudinal tube pitch (along flow direction), the distance between the tube centers along the flow direction. Flow direction refers to the moist air flow.

• l_T is the Transverse tube pitch (perpendicular to flow direction), shown in the figure below. The transverse pitch is the distance between the centers of the two-phase fluid tubing in one row.

• l_D is the diagonal tube spacing, calculated as $$l_{\text{D}}=\sqrt{{\left(\frac{l_{\text{T}}}{2}\right)}^2+l_{\text{L}}^2}.$$

For more information on calculating the Hagen number, see [6].

The longitudinal and transverse pitch distances are the same for both grid bank arrangement types.

Cross-Section of Two-Phase Fluid Tubing with Pitch Measurements

Empirical Nusselt Number Formulation

When the Heat transfer coefficient model is set to Colburn equation or when Flow geometry is set to Generic, the Nusselt number is calculated by the empirical Colburn equation:

$$\text{Nu}=a{\text{Re}}^b{\text{Pr}}^c,$$

where a, b, and c are the values defined in the Coefficients [a, b, c] for a*Re^b*Pr^c parameter.

Pressure Loss for Flow Inside Tubes

When the moist air Flow geometry is set to Flow inside one or more tubes, the pressure loss is calculated the same way as for two-phase flows, with the respective Darcy friction factor, density, mass flow rates, and pipe lengths of the moist air side. See Pressure Loss for more information.

Pressure Loss for Flow Across Tube Banks

When the moist air Flow geometry is set to Flow perpendicular to bank of circular tubes, the Hagen number is used to calculate the pressure loss due to viscous friction. The pressure differential between port A2 and internal node I2 is:

$$p_{\text{A2}}-p_{\text{I2}}=\frac{1}{2}\frac{{\mu }^2{N}_{\text{R}}}{\rho D^2}\text{Hg}(\text{Re}),$$

where:

• μ_MA is the fluid dynamic viscosity.

• N_R is the Number of tube rows along flow direction. This is the number of two-phase fluid tube rows along the moist air flow direction.

The pressure differential between port B2 and internal node I2 is:

$$p_{\text{B2}}-p_{\text{I2}}=\frac{1}{2}\frac{{\mu }^2{N}_{\text{R}}}{\rho D^2}\text{Hg}(\text{Re}).$$

Empirical Pressure Loss Formulation

When the Pressure loss model is set to Euler number per tube row or when Flow geometry is set to Generic, the pressure loss due to viscous friction is calculated with a pressure loss coefficient, in terms of the Euler number, Eu:

$$\text{Eu}=\frac{\xi }{N_R},$$

where ξ is the empirical pressure loss coefficient.

The pressure differential between port A2 and internal node I2 is:

$$p_{\text{A2}}-p_{\text{I2}}=\frac{1}{2}{N}_{R}Eu\frac{{\dot{m}}_{\text{A2}}\left|{\dot{m}}_{\text{A2}}\right|}{2\rho A_{\text{CS}}^2}.$$

The pressure differential between port B2 and internal node I2 is:

$$p_{\text{B2}}-p_{\text{I2}}=\frac{1}{2}{N}_{R}Eu\frac{{\dot{m}}_{\text{B2}}\left|{\dot{m}}_{\text{B2}}\right|}{2\rho A_{\text{CS}}^2}.$$

Conservation Equations

Two-Phase Fluid

The total mass accumulation rate in the two-phase fluid is defined as:

$$\frac{d{M}_{\text{2P}}}{dt}={\dot{m}}_{\text{A1}}+{\dot{m}}_{\text{B1}},$$

where:

• M_2P is the total mass of the two-phase fluid.

• $$\dot{m}$$_A1 is the mass flow rate of the fluid at port A1.

• $$\dot{m}$$_B1 is the mass flow rate of the fluid at port B1.

The flow is positive when flowing into the block through the port.

The energy conservation equation relates the change in specific internal energy to the heat transfer by the fluid:

$$M_{2P}\frac{d{u}_{2P}}{dt}+u_{2P}\left({\dot{m}}_{A1}+{\dot{m}}_{B1}\right)={\varphi }_{\text{A1}}+{\varphi }_{\text{B1}}-Q,$$

where:

• u_2P is the two-phase fluid specific internal energy.

• φ_A1 is the energy flow rate at port A1.

• φ_B1 is the energy flow rate at port B1.

• Q is heat transfer rate, which is positive when leaving the two-phase fluid volume.

Moist Air

The block has mass conversion equations for the moist air mixture, water vapor, trace gas, and water droplets.

Note

If the Trace gas model parameter is None in the Moist Air Properties (MA) block, the moist air network does not model trace gas. In this case, in the Condenser Evaporator (2P-MA) block, the conservation equation for trace gas is set to 0.

If you clear the Enable entrained water droplets in the Moist Air Properties (MA) block, the moist air network does not model entrained water droplets. In this case, in the Condenser Evaporator (2P-MA) block, the conservation equation for water droplets is set to 0.

The accumulation rate for the moist air mixture accounts for the changes of the moist air mass flow through the exchanger ports and the condensation mass flow rate,

$${\dot{m}}_{MA,net}={\dot{m}}_{\text{A2}}+{\dot{m}}_{\text{B2}}-{\dot{m}}_{\text{w,cond}}-{\dot{m}}_{\text{w,conv}}+{\dot{m}}_{\text{d,evap}},$$

where:

• $$\dot{m}$$_A2 is the moist air mass flow rate at port A2.

• $$\dot{m}$$_A2 is the moist air mass flow rate at port B2.

• $$\dot{m}$$_w,cond is the rate of water vapor condensation due to a saturated fluid volume.

• $$\dot{m}$$_w,conv is the rate of condensation on the wall surface.

• $$\dot{m}$$_d,evap is the rate of water droplet evaporation.

The mass conservation equation for water vapor is

$$\frac{d{x}_w}{dt}{\rho }_{M{A}_I}V+x_{\text{w}}{\dot{m}}_{MA,net}={\dot{m}}_{w,net},$$

where x_w is the mass fraction of the vapor, ρ_MAI is the density of the moist air in the fluid volume, and V is the total moist air volume.

$$\dot{m}$$_w,net is the net water vapor mass flow rate,

$${\dot{m}}_{w,net}={\dot{m}}_{\text{w,A2}}+{\dot{m}}_{\text{w,B2}}-{\dot{m}}_{\text{w,cond}}-{\dot{m}}_{\text{w,conv}}+{\dot{m}}_{\text{d,evap}},$$

where:

• $${\dot{m}}_{\text{w,A2}}$$ is the water vapor mass flow rate at port A2.

• $${\dot{m}}_{\text{w,B2}}$$ is the water vapor mass flow rate at port B2.

The trace gas mass balance is

$$\frac{d{x}_{\text{g}}}{dt}{\rho }_{M{A}_I}V+x_{\text{g}}{\dot{m}}_{MA,net}={\dot{m}}_{\text{g,A2}}+{\dot{m}}_{\text{g,B2}},$$

where:

• x_g is the mass fraction of the trace gas.

• $${\dot{m}}_{\text{g,A2}}$$ is the trace gas mass flow rate at port A2.

• $${\dot{m}}_{\text{g,B2}}$$ is the trace gas mass flow rate at port B2.

The water droplet mass balance is

$$\frac{d{r}_{d_I}}{dt}{\rho }_{M{A}_I}V+r_{d_I}{\dot{m}}_{MA,net}={\dot{m}}_{d,net},$$

where r_dI is the mass ratio of the water droplets to the moist air in the fluid volume.

$${\dot{m}}_{d_{net}}$$ is the net water droplet mass flow rate,

$${\dot{m}}_{d,net}={\dot{m}}_{\text{d,A2}}+{\dot{m}}_{\text{d,B2}}+{\lambda }_d\left({\dot{m}}_{\text{w,cond}}+{\dot{m}}_{\text{w,conv}}\right)-{\dot{m}}_{\text{d,evap}},$$

where:

• $$\dot{m}$$_d,A2 is the water droplets mass flow rate at port A2.

• $$\dot{m}$$_d,A2 is the water droplets mass flow rate at port B2.

• λ_d is the value of the Fraction of condensate entrained as water droplets parameter.

On the moist air side, energy conservation accounts for the change in specific internal energy due to heat transfer and water vapor condensing out of the moist air mass,

$$\begin{array}{l}\left(c_{pI}-R_I+r_d{c}_{p_{dI}}\right)V{\rho }_{M{A}_I}\frac{d{T}_I}{dt}+u_{aI}{\dot{m}}_{MA,net}+\left(u_{wI}-u_{aI}\right){\dot{m}}_{w,net}+\left(u_{gI}-u_{aI}\right){\dot{m}}_{g,net}+h_{d_I}{\dot{m}}_{d,net}=\\ {\varphi }_{\text{A2}}+{\varphi }_{\text{B2}}+Q-\left(1-{\lambda }_d\right)\left({\dot{m}}_{\text{w,cond}}{h}_{d_I}+{\dot{m}}_{\text{w,conv}}{h}_{d_H}\right)-p_I\frac{dV}{dt},\end{array}$$

where:

• u_a,I, u_w,I, and u_g,I are the internal energies of the air, water vapor, and gas, respectively.

• c_pI is the moist air specific heat.

• c_pdI is the water droplet specific heat.

• r_d is the mass ratio of water droplets to moist air.

• p_I is the pressure of the internal volume.

• T_I is the temperature of the internal volume.

• R_I is the internal volume specific gas constant.

• h_dI is the water droplet specific enthalpy in the fluid volume.

• h_dH is the water droplet specific enthalpy on the wall surface.

• ϕ_A2 is the energy flow rate at port A2.

• ϕ_B2 is the energy flow rate at port B2.

The heat transferred to or from the moist air, Q, is equal to the heat transferred from or to the thermal liquid.

Examples

Condenser and Evaporator Heat Transfer

Models a condenser or an evaporator in simple test setup with R134a refrigerant on the left side and moist air on the right side. It has a cross flow arrangement with the moist air blowing across tube banks filled with the refrigerant.

• Open Model

Refrigeration Cycle (Air Conditioning)

A refrigeration cycle for a home air conditioning system. See Model a Refrigeration Cycle for the recommended steps to build this model in the two-phase fluid domain.

• Open Model

Ports

Conserving

A1 — Two-phase fluid port

two-phase fluid

Inlet or outlet port associated with the two-phase fluid.

B1 — Two-phase fluid port

two-phase fluid

Inlet or outlet port associated with the two-phase fluid.

A2 — Moist air port

moist air

Inlet or outlet port associated with the moist air.

B2 — Moist air port

moist air

Inlet or outlet port associated with the moist air.

Output

Z — Two-phase fluid zone length fractions

physical signal

Three-element vector of the zone length fractions in the two-phase fluid channel, returned as a physical signal. The vector takes the form [L, M, V], where L is the sub-cooled liquid, M is the liquid-vapor mixture, and V is the superheated vapor.

W — Moist air condensation rate

physical signal

Water condensation rate that leaves the moist air flow, returned as a physical signal. The value of this port does not include the portion of condensation that is entrained as water droplets. The condensate does not accumulate on the heat transfer surface.

Parameters

Configuration

Flow arrangement — Flow path alignment

Cross flow (default) | Parallel flow | Counter flow

Flow path alignment between the heat exchanger sides. The available flow arrangements are:

• Parallel flow. The flows run in the same direction.

• Counter flow. The flows run parallel to each other, in the opposite directions.

• Cross flow. The flows run perpendicular to each other.

Cross flow arrangement — Thermal mixing condition

Two-Phase Fluid 1 unmixed & Moist Air 2 mixed (default) | Both fluids unmixed | Two-phase fluid 1 mixed & Moist Air 2 unmixed | Both fluids mixed

Select whether each of the fluids can mix in its channel. Mixed flow means that the fluid is free to move in the transverse direction as it travels along the flow path. Unmixed flow means that the fluid is restricted to travel only along the flow path. For example, a side with fins is considered an unmixed flow.

Dependencies

To enable this parameter, set Flow arrangement to Cross flow.

Thermal resistance through heat transfer surface — Wall thermal resistance

0 K/kW (default) | positive scalar

Thermal resistance of the wall that separates the two sides of the heat exchanger. The wall thermal resistance, wall fouling, and fluid convective heat transfer coefficient influence the amount of heat transferred between the flows.

Cross-sectional area at port A1 — Flow area at port A1

0.01 m^2 (default) | positive scalar

Flow area at the two-phase fluid port A1.

Cross-sectional area at port B1 — Flow area at port B1

0.01 m^2 (default) | positive scalar

Flow area at the two-phase fluid port B1.

Cross-sectional area at port A2 — Flow area at port A2

0.01 m^2 (default) | positive scalar

Flow area at the moist air side port A2.

Cross-sectional area at port B2 — Area normal to flow at port B2

0.01 m^2 (default) | positive scalar

Flow area at the moist air side port B2.

Two-Phase Fluid 1

Number of tubes — Number of two-phase fluid tubes

25 (default) | positive scalar

Number of two-phase fluid tubes.

Total length of each tube — Total length of each two-phase fluid tube

1 m (default) | positive scalar

Total length of each two-phase fluid tube.

Tube cross section — Cross-sectional shape of a tube

Circular (default) | Rectangular | Annular | Generic

Cross-sectional shape of a tube. Use Generic to specify an arbitrary cross-sectional geometry.

This parameter specifies the cross-section of one tube.

Tube inner diameter — Internal diameter of a single tube

0.05 m (default) | positive scalar

Internal diameter of the cross-section of one tube. The cross-section and diameter are uniform along the tube. The size of the diameter influences the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Tube cross-section to Circular.

Tube width — Internal width of a single tube

0.05 m (default) | positive scalar

Internal width of the cross-section of one tube. The cross-section and width are uniform along the tube. The width and height influence the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Tube cross-section to Rectangular.

Tube height — Internal height of a single tube

0.05 m (default) | positive scalar

Internal height of one tube. The cross-section and height are uniform along the tube. The width and height influence the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Tube cross-section to Rectangular.

Annulus inner diameter (heat transfer surface) — Smaller diameter of annular cross-section

0.05 m (default) | positive scalar

Smaller diameter of the annular cross-section of one tube. The cross-section and inner diameter are uniform along the tube. The inner diameter influences the pressure loss and heat transfer calculations. Heat transfer occurs through the inner surface of the annulus.

Dependencies

To enable this parameter, set Tube cross-section to Annular.

Annulus outer diameter — Larger diameter of annular cross-section

0.1 m (default) | positive scalar

Larger diameter of the annular cross-section of one tube. The cross-section and outer diameter are uniform along the tube. The outer diameter influences the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Tube cross-section to Annular.

Cross-sectional area per tube — Internal area normal to flow in a single tube

0.002 m^2 (default) | positive scalar

Internal flow area of each tube.

Dependencies

To enable this parameter, set Tube cross-section to Generic.

Wetted perimeter of tube cross-section for pressure loss — Perimeter of tube cross-section that fluid touches

0.15 m (default) | positive scalar

Perimeter of the tube cross-section that the fluid touches. The cross-section and perimeter are uniform along the tube. This value is applied in pressure loss calculations.

Dependencies

To enable this parameter, set Tube cross-section to Generic.

Perimeter of tube cross-section for heat transfer — Perimeter of a single tube for heat transfer calculations

0.15 m (default) | positive scalar

Tube perimeter for heat transfer calculations. This is often the same as the tube perimeter, but in cases such as the annular cross-section, this may be only the inner or outer diameter, depending on the heat-transferring surface. The cross-section and tube perimeter are uniform along the tube.

Dependencies

To enable this parameter, set Tube cross-section to Generic.

Pressure loss model — Method of pressure loss calculation due to viscous friction

Correlation for flow inside tubes (default) | Pressure loss coefficient

Method of pressure loss calculation due to viscous friction. The settings are:

• Pressure loss coefficient. Use this setting to calculate the pressure loss based on an empirical loss coefficient.

• Correlation for flow inside tubes. Use this setting to calculate the pressure loss based on the pipe flow correlation.

Pressure loss coefficient, delta_p/(0.5*rho*v^2) — Empirical loss coefficient for all pressure losses in channel

10 (default)

Empirical loss coefficient for all pressure losses in the channel. This value accounts for wall friction and minor losses due to bends, elbows, and other geometry changes in the channel.

The loss coefficient can be calculated from a nominal operating condition or be tuned to fit experimental data. The loss coefficient is defined as:

$$\xi =\frac{\Delta p}{\frac{1}{2}\rho v^2},$$

where Δp is the pressure drop, ρ is the two-phase fluid density, and v is the flow velocity.

Dependencies

To enable this parameter, set Pressure loss model to Pressure loss coefficient.

Local resistance specification — Method for quantifying pressure losses

Aggregate equivalent length (default) | Local loss coefficient

Method for quantifying pressure losses in the Haaland correlation.

Dependencies

To enable this parameter, set Pressure loss model to Correlation for flow inside tubes.

Total local loss coefficient — Pressure loss coefficient

0.1 (default) | positive scalar

Local pressure loss coefficient over the system. You can use this parameter to calibrate your system to match experimental results.

Dependencies

To enable this parameter, set Pressure loss model to Correlation for flow inside tubes and Local resistance specification to Local loss coefficient.

Aggregate equivalent length of local resistances — Combined length of all local resistances per tube

0.1 m (default) | positive scalar

Combined length of all local resistances per tube. This value is the length of tubing that results in the same pressure losses as the sum of all minor losses in the tube due to resistances such as bends, tees, or unions. A longer combined length results in larger pressure losses. The block adds the value of this parameter to the Total length of each tube parameter in the calculations of pressure loss due to friction.

Dependencies

To enable this parameter, set Pressure loss model to Correlation for flow inside tubes and Local resistance specification to Aggregate equivalent length.

Internal surface absolute roughness — Mean surface roughness height

15e-6 m (default) | positive scalar

Mean height of tube surface defects. A rougher wall results in larger pressure losses in the turbulent regime for pressure loss calculated with the Haaland correlation.

Dependencies

To enable this parameter, set either:

• Pressure loss model

• Heat transfer model

to Correlation for flow inside tubes.

Laminar flow upper Reynolds number limit — Largest Reynolds number that indicates laminar flow

2000 (default) | positive scalar

Largest Reynolds number that indicates laminar flow. Between this value and the Turbulent flow lower Reynolds number, the flow regime is transitional.

Turbulent flow lower Reynolds number limit — Smallest Reynolds number that indicates turbulent flow

4000 (default) | positive scalar

Smallest Reynolds number that indicates turbulent flow. Between this value and the Laminar flow upper Reynolds number limit, the flow regime is transitional.

Laminar friction constant for Darcy friction factor — Coefficient of pressure loss due to viscous friction in laminar flows

64 (default) | positive scalar

Coefficient in pressure loss equations for viscous friction in laminar flows. This parameter may also be known as the shape factor. The default value corresponds to a circular tube cross-section.

Dependencies

To enable this parameter, set Tube cross section to Generic and Pressure loss model to Correlation for flow inside tubes.

Heat transfer coefficient model — Method of calculating heat transfer coefficient between fluid and wall

Correlation for flow inside tubes (default) | Colburn equation

Method of calculating the heat transfer coefficient between the fluid and the wall. The available settings are:

• Colburn equation. Use this setting to calculate the heat transfer coefficient with user-defined variables a, b, and c. In the liquid and vapor zones, the heat transfer coefficient is based on the Colburn equation. In the liquid-vapor mixture zone, the heat transfer coefficient is based on the Cavallini-Zecchin equation.

• Correlation for flow inside tubes. Use this setting to calculate the heat transfer coefficient for pipe flows. In the liquid and vapor zones, the heat transfer coefficient is calculated with the Gnielinski correlation. In the liquid-vapor mixture zone, the heat transfer coefficient is calculated with the Cavallini-Zecchin equation.

Coefficients [a, b, c] for a*Re^b*Pr^c in liquid zone — Colburn equation coefficients in liquid zone

[.023, .8, .33] (default) | three-element vector of positive scalars

Three-element vector that contains the empirical coefficients of the Colburn equation. Each fluid zone has a distinct Nusselt number, which the block calculates by using the Colburn equation for each zone. The general form of the Colburn equation is:

$$\text{Nu}=a{\text{Re}}^b{\text{Pr}}^c.$$

Dependencies

To enable this parameter, set Heat transfer coefficient model to Colburn equation.

Coefficients [a, b, c] for a*Re^b*Pr^c in mixture zone — Cavallini-Zecchin equation coefficients in mixture zone

[.05, .8, .33] (default) | three-element vector of positive scalars

Three-element vector that contains the empirical coefficients for the Cavallini-Zecchin equation. Each fluid zone has a distinct Nusselt number, which the block calculates in the mixture zone by using the Cavallini-Zecchin equation:

$$\text{Nu}=\frac{{\text{aRe}}_{\text{SL}}^b{\text{Pr}}_{\text{SL}}^c\left\{{\left[\left(\sqrt{\frac{{\rho }_{\text{SL}}}{{\rho }_{\text{SV}}}}-1\right)x_{\text{Out}}+1\right]}^{1+b}-{\left[\left(\sqrt{\frac{{\rho }_{\text{SL}}}{{\rho }_{\text{SV}}}}-1\right)x_{\text{In}}+1\right]}^{1+b}\right\}}{\left(1+b\right)\left(\sqrt{\frac{{\rho }_{\text{SL}}}{{\rho }_{\text{SV}}}}-1\right)(x_{\text{Out}}-x_{\text{In}})}.$$

Dependencies

To enable this parameter, set Heat transfer coefficient model to Colburn equation.

Coefficients [a, b, c] for a*Re^b*Pr^c in vapor zone — Colburn equation coefficients in vapor zone

[.023, .8, .33] (default) | three-element vector of positive scalars

Three-element vector that contains the empirical coefficients of the Colburn equation. Each fluid zone has a distinct Nusselt number, which the block calculates by using the Colburn equation for each zone. The general form of the Colburn equation is:

$$\text{Nu}=a{\text{Re}}^b{\text{Pr}}^c.$$

Dependencies

To enable this parameter, set Heat transfer coefficient model to Colburn equation.

Laminar flow Nusselt number — Ratio of convective to conductive heat transfer in the laminar flow regime

3.66 (default) | positive scalar

Ratio of convective to conductive heat transfer in the laminar flow regime. The fluid Nusselt number influences the heat transfer rate and depends on the tube cross-section.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Correlation for flow inside tubes.

Fouling factor — Additional thermal resistance due to fouling deposits

0.1 m^2*K/kW (default) | positive scalar

Additional thermal resistance due to fouling layers on the surfaces of the wall. In real systems, fouling deposits grow over time. However, the growth is slow enough to be assumed constant during the simulation.

Total fin surface area — Total heat transfer surface area of fins

0 m^2 (default) | positive scalar

Total heat transfer surface area of both sides of all fins touching the two-phase fluid. For example, if the fin is rectangular, the surface area is double the area of the rectangle.

The total heat transfer surface area is the sum of the channel surface area and the effective fin surface area, which is the product of the Fin efficiency and the Total fin surface area.

Fin efficiency — Ratio of actual-to-ideal transfer rates for fin

0.5 (default) | positive scalar in the range [0,1]

Ratio of actual heat transfer to ideal heat transfer through the fins touching the two-phase fluid if the entire fin is at the primary heat transfer surface temperature.

Initial fluid energy specification — Initial state of the two-phase fluid

Temperature (default) | Vapor quality | Vapor void fraction | Specific enthalpy | Specific internal energy

Quantity used to describe the initial state of the fluid.

The value for Initial fluid energy specification parameter limits the available initial states for the two-phase fluid. When Initial fluid energy specification is:

• Temperature — Specify an initial state that is a subcooled liquid or superheated vapor. You cannot specify a liquid-vapor mixture because the temperature is constant across the liquid-vapor mixture region.

• Vapor quality — Specify an initial state that is a liquid-vapor mixture. You cannot specify a subcooled liquid or a superheated vapor because the liquid mass fraction is 0 and 1, respectively, across the whole region. Additionally, the block limits the pressure to below the critical pressure.

• Vapor void fraction — Specify an initial state that is a liquid-vapor mixture. You cannot specify a subcooled liquid or a superheated vapor because the liquid mass fraction is 0 and 1, respectively, across the whole region. Additionally, the block limits the pressure to below the critical pressure.

• Specific enthalpy — Specify the specific enthalpy of the fluid. The block does not limit the initial state.

• Specific internal energy — Specify the specific internal energy of the fluid. The block does not limit the initial state.

Initial two-phase fluid pressure — Fluid pressure at start of simulation

0.101325 MPa (default) | positive scalar

Fluid pressure at the start of the simulation.

Initial two-phase fluid temperature — Temperature at start of simulation

293.15 K (default) | positive scalar | two-element vector

Temperature in the two-phase fluid channel at the start of simulation. This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial temperature in the channel. A vector value represents the initial temperature at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial fluid energy specification to Temperature.

Initial two-phase fluid vapor quality — Vapor mass fraction at start of simulation

0.5 (default) | positive scalar in the range [0,1] | two-element vector

Vapor mass fraction in the two-phase fluid channel at the start of simulation. This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial vapor quality in the channel. A vector value represents the initial vapor quality at the inlet and outlet in the form [inlet, outlet]]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial fluid energy specification to Vapor quality.

Initial two-phase fluid vapor void fraction — Vapor volume fraction at start of simulation

0.5 (default) | positive scalar in the range [0,1] | two-element vector

Vapor volume fraction in the two-phase fluid channel at the start of simulation. This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial void fraction in the channel. A vector value represents the initial void fraction at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial fluid energy specification to Vapor void fraction.

Initial two-phase fluid specific enthalpy — Enthalpy per unit mass at start of simulation

1500 kJ/kg (default) | positive scalar | two-element vector

Enthalpy per unit mass in the two-phase fluid channel at the start of simulation. This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial specific enthalpy in the channel. A vector value represents the initial specific enthalpy at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial fluid energy specification to Specific enthalpy.

Initial two-phase fluid specific internal energy — Internal energy per unit mass at start of simulation

1500 kJ/kg (default) | positive scalar | two-element vector

Internal energy per unit mass in the two-phase fluid channel at the start of simulation. This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial specific internal energy in the channel. A vector value represents the initial specific internal energy at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial fluid energy specification to Specific internal energy.

Moist Air 2

Flow geometry — Moist air flow configuration

Flow perpendicular to bank of circular tubes (default) | Flow inside one or more tubes | Generic

Moist air flow path. The flow can run externally over a set of tubes or internal to a tube or set of tubes. You can also specify a generic parameterization based on empirical values.

Number of tubes — Number of moist air tubes

25 (default) | positive scalar

Number of moist air tubes. More tubes result in higher pressure losses due to viscous friction, but a larger amount of surface area for heat transfer.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes.

Total length of each tube — Total length of each moist air tube

1 m (default) | positive scalar

Total length of each moist air tube.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes.

Tube cross section — Cross-sectional shape of a tube

Circular (default) | Rectangular | Annular | Generic

Cross-sectional shape of one tube. Set to Generic to specify an arbitrary cross-sectional geometry.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes.

Tube inner diameter — Internal diameter of a single tube

0.05 m (default) | positive scalar

Internal diameter of the cross-section of one tube. The cross-section and diameter are uniform along the tube. The size of the diameter influences the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Tube cross-section to Circular.

Tube width — Internal width of a single tube

0.05 m (default) | positive scalar

Internal width of the cross-section of one tube. The cross-section and width are uniform along the tube. The width and height influence the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Tube cross-section to Rectangular.

Tube height — Internal height of a single tube

0.05 m (default) | positive scalar

Internal height of one tube cross-section. The cross-section and height are uniform along the tube. The width and height influence the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Flow geometry parameterization of Flow inside one or more tubes and Tube cross-section to Rectangular.

Annulus inner diameter (heat transfer surface) — Smaller diameter of annular cross-section

0.05 m (default) | positive scalar

Smaller diameter of the annular cross-section of one tube. The cross-section and inner diameter are uniform along the tube. The inner diameter influences the pressure loss and heat transfer calculations. Heat transfer occurs through the inner surface of the annulus.

Dependencies

To enable this parameter, set Flow geometry parameterization of Flow inside one or more tubes and Tube cross-section to Annular.

Annulus outer diameter — Larger diameter of annular cross-section

0.1 m (default) | positive scalar

Larger diameter of the annular cross-section of one tube. The cross-section and outer diameter are uniform along the tube. The outer diameter influences the pressure loss and heat transfer calculations.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Tube cross-section to Annular.

Cross-sectional area per tube — Internal flow area in each tube

0.002 m^2 (default) | positive scalar

Internal flow area of each tube.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Tube cross-section to Generic.

Wetted perimeter of tube cross-section for pressure loss — Perimeter of tube cross-section that fluid touches

0.15 m (default) | positive scalar

Perimeter of the tube cross-section that the fluid touches. The cross-section and perimeter are uniform along the tube. This value is applied in pressure loss calculations.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Tube cross-section to Generic.

Perimeter of tube cross-section for heat transfer — Perimeter of a single tube for heat transfer calculations

0.15 m (default) | positive scalar

Tube perimeter for heat transfer calculations. This is often the same as the tube perimeter, but in cases such as the annular cross-section, this may be only the inner or outer diameter, depending on the heat-transferring surface. The cross-section and tube perimeter are uniform along the tube.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Tube cross-section to Generic.

Pressure loss model — Method of pressure loss calculation due to viscous friction

Correlation for flow inside tubes (default) | Euler number per tube row | Pressure loss coefficient | Correlation for flow over tube bank

Method of pressure loss calculation due to viscous friction. Different models are available for different flow configurations. The settings are:

• Correlation for flow inside tubes. Use this setting to calculate the pressure loss with the Haaland correlation.

• Pressure loss coefficient. Use this setting to calculate the pressure loss based on an empirical loss coefficient.

• Euler number per tube row. Use this setting to calculate the pressure loss based on an empirical Euler number.

• Correlation for flow over tube bank. Use this setting to calculate the pressure loss based on the Hagen number.

The pressure loss models available depend on the Flow geometry setting.

Dependencies

When Flow geometry is set to Flow inside one or more tubes, Pressure loss model can be set to either:

• Pressure loss coefficient.

• Correlation for flow inside tubes.

When Flow geometry is set to Flow perpendicular to bank of circular tubes, Pressure loss model can be set to either:

• Correlation for flow over tube bank.

• Euler number per tube row.

When Flow geometry is set to Generic, the Pressure loss model parameter is disabled. Pressure loss is calculated empirically with the Pressure loss coefficient, delta_p/(0.5*rho*v^2) parameter.

Pressure loss coefficient, delta_p/(0.5*rho*v^2) — Empirical loss coefficient for all pressure losses in the channel

10 (default) | positive scalar

Empirical loss coefficient for all pressure losses in the channel. This value accounts for wall friction and minor losses due to bends, elbows, and other geometry changes in the channel.

The loss coefficient can be calculated from a nominal operating condition or be tuned to fit experimental data. The pressure loss coefficient is defined as:

$$\xi =\frac{\Delta p}{\frac{1}{2}\rho v^2},$$

where Δp is the pressure drop, ρ is the two-phase fluid density, and v is the flow velocity.

Dependencies

To enable this parameter, set either:

• Flow geometry to Generic.

• Pressure loss model to Pressure loss coefficient.

Local resistance specification — Method for quantifying pressure losses

Aggregate equivalent length (default) | Local loss coefficient

Method for quantifying pressure losses in the Haaland correlation.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Pressure loss model to Correlation for flow inside tubes.

Total local loss coefficient — Pressure loss coefficient

0.1 (default) | positive scalar

Local pressure loss coefficient over the system. You can use this parameter to calibrate your system to match experimental results.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes, Pressure loss model to Correlation for flow inside tubes, and Local resistance specification to Local loss coefficient.

Aggregate equivalent length of local resistances — Combined length of all local resistances per tube

0.1 m (default) | positive scalar

Combined length of all local resistances per tube. This value is the length of tubing that results in the same pressure losses as the sum of all minor losses in the tube due to resistances such as bends, tees, or unions. A longer combined length results in larger pressure losses. The block adds the value of this parameter to the Total length of each tube parameter in the calculations of pressure loss due to friction.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes, Pressure loss model to Correlations for flow inside tubes, and Local resistance specification to Aggregate equivalent length.

Internal surface absolute roughness — Mean surface roughness height

15e-6 m (default) | positive scalar

Mean height of tube surface defects. A rougher wall results in larger pressure losses in the turbulent regime for pressure loss calculated with the Haaland correlation.

Dependencies

To enable this parameter, set either:

• Pressure loss model

• Heat transfer coefficient model

to Correlation for flow inside tubes.

Laminar flow upper Reynolds number limit — Largest Reynolds number that indicates laminar flow

2000 (default) | positive scalar

Largest Reynolds number that indicates laminar flow. Between this value and the Turbulent flow lower Reynolds number limit, the flow regime is transitional.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Pressure loss model to Correlation for flow inside tubes.

Turbulent flow lower Reynolds number limit — Smallest Reynolds number that indicates turbulent flow

4000 (default) | positive scalar

Smallest Reynolds number that indicates turbulent flow. Between this value and the Laminar flow upper Reynolds number limit, the flow regime is transitional between the laminar and turbulent regimes.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes and Pressure loss model to Correlation for flow inside tubes.

Laminar friction constant for Darcy friction factor — Coefficient of pressure loss due to viscous friction in laminar flows

64 (default) | positive scalar

Coefficient in pressure loss equations for viscous friction in laminar flows. This parameter is also known as the shape factor. The default value corresponds to a circular tube cross-section.

Dependencies

To enable this parameter, set Flow geometry to Correlation for flow inside tubes, Tube cross section to Generic, and Pressure loss model to Correlation for flow inside tubes.

Heat transfer coefficient model — Method of calculating heat transfer coefficient between fluid and wall

Correlation for flow over tube bank (default) | Colburn equation | Correlation for flow inside tubes

Method of calculating the heat transfer coefficient between the fluid and the wall. The available settings are:

• Colburn equation. Use this setting to calculate the heat transfer coefficient with user-defined variables a, b, and c of the Colburn equation.

• Correlation for flow over tube bank. Use this setting to calculate the heat transfer coefficient based on the tube bank correlation using the Hagen number.

• Correlation for flow inside tubes. Use this setting to calculate the heat transfer coefficient for pipe flows with the Gnielinski correlation.

Dependencies

To enable this parameter, set Flow geometry to either:

• Flow perpendicular to bank of circular tubes.

• Flow inside one or more tubes.

Coefficients [a, b, c] for a*Re^b*Pr^c — Colburn equation coefficients

[0.023, 0.8, 0.33] (default) | three-element vector

Three-element vector containing the empirical coefficients of the Colburn equation. The Colburn equation is a formulation for calculating the Nusselt Number. The general form of the Colburn equation is:

$$\text{Nu}=a{\text{Re}}^b{\text{Pr}}^c.$$

When the Heat transfer coefficient model is set to Colburn equation and Flow geometry is set to Flow inside one or more tubes, or Flow geometry is set to Generic, the default Colburn equation is:

$$\text{Nu}=0.023{\text{Re}}^{0.8}{\text{Pr}}^{1/3}.$$

When the Heat transfer coefficient model is set to Colburn equation and Flow geometry is set to Flow perpendicular to bank of circular tubes, the default Colburn equation is:

$$\text{Nu}=0.27{\text{Re}}^{0.63}{\text{Pr}}^{0.36}.$$

Dependencies

To enable this parameter, set:

1. Flow geometry to either:

   • Flow inside one or more tubes

   • Flow perpendicular to bank of circular tubes

   and Heat transfer coefficient model to Colburn equation.

2. Flow geometry to Generic.

Laminar flow Nusselt number — Ratio of convective to conductive heat transfer in laminar flow regime

3.66 (default) | positive scalar

Ratio of convective to conductive heat transfer in the laminar flow regime. The fluid Nusselt number influences the heat transfer rate and depends on the tube cross-section.

Dependencies

To enable this parameter, set Flow geometry to Flow inside one or more tubes, Tube cross-section to Generic, and Heat transfer parameterization to Correlation for flow inside tubes.

Tube bank grid arrangement — Geometrical placement of tube rows in the bank

Inline (default) | Staggered

Alignment of tubes in a tube bank. Rows are either in line with their neighbors, or staggered.

• Inline: All tube rows are located directly behind each other.

• Staggered: Tubes of the one tube row are located at the gap between tubes of the previous tube row.

Tube alignment influences the Nusselt number and the heat transfer rate.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes.

Number of tube rows along flow direction — Number of tube rows in tube bank

5 (default) | positive scalar

Number of two-phase fluid tube rows in a tube bank. The rows are aligned with the direction of moist air flow.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes.

Number of tube segments in each tube row — Number of two-phase fluid tubes in each row of the tube bank

5 (default) | positive scalar

Number of two-phase fluid tubes in each row of a tube bank. This measurement is perpendicular to the moist air flow.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes.

Length of each tube segment in a tube row — Length of each two-phase fluid tube

1 m (default) | positive scalar

Length of each two-phase fluid tube that spans a tube row. All tubes in a tube bank are the same length.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes.

Tube outer diameter — Outer diameter of a single two-phase fluid tube

0.05 m (default) | positive scalar

Outer diameter of a two-phase fluid tube. The cross-section is uniform along a tube and so the diameter is constant throughout. This value influences the losses in the flow across a tube bank due to viscous friction.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes.

Longitudinal tube pitch (along flow direction) — Center-to-center distance between two-phase fluid tube rows

0.15 m (default) | positive scalar

Distance between tube centers of the two-phase fluid tubes, aligned with the direction of flow of the moist air.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes.

Transverse tube pitch (perpendicular to flow direction) — Center-to-center distance between two-phase fluid tubes in a row

0.15 m (default) | positive scalar

Distance between the tube centers in a row of two-phase fluid tubes. This measurement is perpendicular to the moist air flow direction. See Heat Transfer Coefficient for Flows Across a Tube Bank for more information.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes.

Euler number per tube row, delta_p/(N*0.5*rho*v^2) — Euler number for each row of the tube bank

10 (default) | positive scalar

Empirical coefficient for pressure drop across one tube row. The Euler number is the ratio between pressure drop and fluid momentum:

$$\text{Eu}=\frac{\Delta p}{N\frac{1}{2}\rho v^2},$$

where N is the Number of tube rows along flow direction, Δp is the pressure drop, ρ is the moist air mixture density, and v is the flow velocity.

Each tube row is located in a plane perpendicular to the moist air flow.

Dependencies

To enable this parameter, set Flow geometry to Flow perpendicular to bank of circular tubes and Pressure loss model to Euler number per tube row.

Minimum free-flow area — Smallest total flow area between inlet and outlet

0.01 m^2 (default) | positive scalar

Smallest total cross-sectional flow area between inlet and outlet. If the channel is a collection of ducts, tubes, slots, or grooves, the value of this parameter is the sum of the smallest areas at the minimum flow area point. This parameter is the area where the fluid velocity is highest. For example, if the fluid flows perpendicular to a bank of tubes, the value of this parameter is the sum of the gaps between the tubes in one cross-section where the sum of the gaps is smallest is smallest.

Dependencies

To enable this parameter, set Flow geometry to Generic.

Heat transfer surface area without fins — Total area of the heat transfer surface excluding fins

2 m^2 (default) | positive scalar

Total area of the heat transfer surface, excluding fins.

Dependencies

To enable this parameter, set Flow geometry to Generic.

Moist air volume inside heat exchanger — Total volume of moist air in the heat exchanger

0.05 m^3 (default) | positive scalar

Total volume of moist air in the heat exchanger.

Dependencies

To enable this parameter, set Flow geometry to Generic.

Fouling factor — Additional thermal resistance due to fouling deposits

0.1 m^2*K/kW (default) | positive scalar

Additional thermal resistance due to fouling layers on the surfaces of the wall. In real systems, fouling deposits grow over time. However, the growth is slow enough to be assumed constant during the simulation.

Total fin surface area — Total heat transfer surface area of all fins

0 m^2 (default) | positive scalar

Total heat transfer surface area of both sides of all fins touching the moist air. For example, if the fin is rectangular, the surface area is double the area of the rectangle.

The total heat transfer surface area is the sum of the channel surface area and the effective fin surface area, which is the product of the Fin efficiency and the Total fin surface area.

Fin efficiency — Ratio of actual-to-ideal transfer rates for fin

0.5 (default) | positive scalar in the range [0,1]

Ratio of actual heat transfer to ideal heat transfer through the fins touching the moist air if the entire fin is at the primary heat transfer surface temperature.

Initial moist air pressure — Moist air pressure at start of simulation

0.101325 MPa (default) | positive scalar

Moist air pressure at the start of the simulation.

Initial moist air temperature — Temperature at the start of simulation

293.15 K (default) | positive scalar | two-element vector

Temperature in the moist air fluid channel at the start of the simulation. This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial temperature in the channel. A vector value represents the initial temperature at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Initial humidity specification — Humidity specification

Relative humidity (default) | Specific humidity | Mole fraction | Humidity ratio | Wet-bulb temperature

Initial humidity specification on the moist air side.

Initial moist air relative humidity — Relative humidity at the start of simulation

0.5 (default) | positive scalar in the range of [0,1] | two-element vector

Relative humidity in the moist air channel at the start of the simulation. The relative humidity is the ratio of the water vapor partial pressure to the water vapor saturation pressure, or the ratio of the water vapor mole fraction to the water vapor mole fraction at saturation.

This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial relative humidity in the channel. A vector value represents the initial relative humidity at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial humidity specification to Relative humidity.

Initial moist air specific humidity — Specific humidity at the start of simulation

0.01 (default) | positive scalar in the range of [0,1] | two-element vector

Specific humidity in the moist air channel at the start of simulation. The specific humidity is the mass fraction of water vapor to the combined total mass of water vapor, trace gas, and dry air.

This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial specific humidity in the channel. A vector value represents the initial specific humidity at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial humidity specification to Specific humidity.

Initial moist air water vapor mole fraction — Mole fraction of water vapor at the start of simulation

0.01 (default) | positive scalar in the range [0,1] | two-element vector

Mole fraction of the water vapor in the moist air channel at the start of simulation. The water vapor mole fraction is relative to the combined molar quantity of water vapor, trace species, and dry air.

This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial vapor mole fraction in the channel. A vector value represents the initial vapor mole fraction at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial humidity specification to Mole fraction.

Initial moist air humidity ratio — Humidity ratio at the start of simulation

0.01 (default) | positive scalar in the range [0,1] | two-element vector

Humidity ratio in the moist air channel at the start of the simulation. The humidity ratio is the ratio of the mass of water vapor to the mass of dry air and trace gas.

This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial humidity ratio in the channel. A vector value represents the initial humidity ratio at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial humidity specification to Humidity ratio.

Initial moist air wet-bulb temperature — Wet-bulb temperature at the start of simulation

287 K (default) | positive scalar in the range [0,1]

Wet-bulb temperature at the start of the simulation. The block uses this value to calculate the humidity.

This parameter can be a scalar or a two-element vector. A scalar value represents the mean initial wet-bulb temperature in the channel. A vector value represents the initial wet-bulb temperature at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

Dependencies

To enable this parameter, set Initial humidity specification to Wet-bulb temperature.

Initial trace gas specification — Measurement type of trace gas

Mass fraction (default) | Mole fraction

Measurement type of trace gas.

Initial moist air trace gas mass fraction — Amount of trace gas in the moist air channel

0.001 (default) | positive scalar in the range of [0,1] | two-element vector

Amount of trace gas in the moist air channel by mass fraction at the start of the simulation. The mass fraction is relative to the combined total mass of water vapor, trace gas, and dry air.

This parameter can be a scalar or a two-element vector. A scalar value represents the mean trace gas mass fraction in the channel. A vector value represents the initial trace gas mass fraction at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

This parameter is ignored if the Trace gas model parameter in the Moist Air Properties (MA) block is set to None.

Dependencies

To enable this parameter, set Initial trace gas specification to Mass fraction.

Initial moist air trace gas mole fraction — Mole fraction of trace gas at the start of simulation

0.001 (default) | positive scalar in the range of [0,1] | two-element vector

Amount of trace gas in the moist air channel by mole fraction at the start of the simulation. The mole fraction is relative to the combined molar total of water vapor, trace gas, and dry air.

This parameter can be a scalar or a two-element vector. A scalar value represents the mean trace gas mole fraction in the channel. A vector value represents the initial trace gas mole fraction at the inlet and outlet in the form [inlet, outlet]. The block calculates a linear gradient between the two ports. The inlet and the outlet ports are identified according to the initial flow direction.

This parameter is ignored if the Trace gas model parameter in the Moist Air Properties (MA) block is set to None.

Dependencies

To enable this parameter, set Initial trace gas specification to Mole fraction.

Initial mass ratio of water droplets to moist air — Ratio of water droplets to moist air

0 (default) | positive scalar

Initial mass ratio of water droplets to moist air.

Relative humidity at saturation — Relative humidity point of condensation

1 (default) | positive scalar in the range of [0,1]

Relative humidity point of condensation. Condensation occurs above this value. A value greater than 1 indicates a supersaturated vapor.

Water vapor condensation time constant — Time scale for condensation

1e-3 s (default) | positive scalar

Characteristic time scale at which an oversaturated moist air volume returns to saturation by condensing out excess humidity.

Water droplets evaporation time constant — Time scale for evaporation

1e-3 s (default) | positive scalar

Characteristic time scale at which water droplets evaporate to vapor.

Fraction of condensate entrained as water droplets — Fraction of condensate in water droplets

1 (default) | scalar in the range [0,1]

Fraction of the condensate in the moist air that is entrained as water droplets.

References

[1] 2013 ASHRAE Handbook - Fundamentals. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., 2013.

[2] Braun, J. E., S. A. Klein, and J. W. Mitchell. "Effectiveness Models for Cooling Towers and Cooling Coils." ASHRAE Transactions 95, no. 2, (June 1989): 164–174.

[3] Çengel, Yunus A. Heat and Mass Transfer: A Practical Approach. 3rd ed, McGraw-Hill, 2007.

[4] Ding, X., Eppe J.P., Lebrun, J., Wasacz, M. "Cooling Coil Model to be Used in Transient and/or Wet Regimes. Theoretical Analysis and Experimental Validation." Proceedings of the Third International Conference on System Simulation in Buildings (1990): 405-411.

[5] Mitchell, John W., and James E. Braun. Principles of Heating, Ventilation, and Air Conditioning in Buildings. Wiley, 2013.

[6] Shah, R. K., and Dušan P. Sekulić. Fundamentals of Heat Exchanger Design. John Wiley & Sons, 2003.

[7] White, Frank M. Fluid Mechanics. 6th ed, McGraw-Hill, 2009.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2019a

R2024b: Model water droplets suspended in moist air flow

Blocks in the moist air domain can now model water droplets suspended in a moist air flow. To model water droplets, select Enable entrained water droplets in the Moist Air Properties (MA) block connected to your moist air network.

R2024a: Update to free-flow area calculation

The block now uses a different method to calculate the free-flow area when Flow geometry is Flow perpendicular to bank of circular tubes. If the value of the Number of tube segments in each tube row parameter is small, the block may show a slight increase in pressure loss and heat transfer.

R2024a: New moisture specification option

The block has a new option for the Initial humidity specification parameter. This option, called Wet-bulb temperature, allows you to input data in the form of a wet-bulb temperature.

R2023a: Model additional pressure losses by using a local loss coefficient

Set the Local resistance specification parameter to Local loss coefficient to specify the new method for quantifying pressure loss. This option allows you to model additional friction losses beyond the loss due the length of the pipes.