Spring-Loaded Accumulator (IL)
Accumulator with a spring used for energy storage in an isothermal liquid system
Libraries:
Simscape /
Fluids /
Isothermal Liquid /
Tanks & Accumulators
Description
This block models a spring-charged accumulator in an isothermal liquid network. The accumulator consists of a preloaded spring and a liquid chamber.
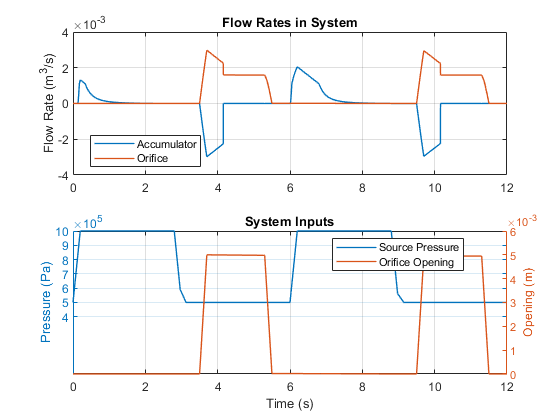
As the liquid pressure at the accumulator inlet becomes greater than the preload pressure, liquid enters the accumulator and compresses the spring. A decrease in the liquid pressure causes the spring to decompress and discharge stored liquid into the system. The separator motion is restricted by a hard stop when the liquid volume is zero and when the liquid volume is at the liquid chamber capacity.
The inlet liquid resistance and spring properties, such as the spring inertia and damping, are not modeled. The spring pressure is assumed to be linear with respect to the liquid volume. The flow rate is positive if liquid flows into the accumulator.
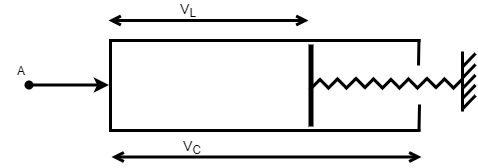
This diagram represents a spring-loaded accumulator.
VL | Volume of the liquid in the accumulator. |
VC | Liquid chamber capacity |
pmax | Pressure at full capacity |
pI | Liquid pressure in the liquid chamber, which is equal to the pressure at the accumulator inlet. |
pHS | Hard-stop contact pressure. |
Kstiff | Hard-stop stiffness coefficient. |
Kspring | Spring gain. |
A | Mass flow rate of liquid coming into port A. |
ρI | Density of the liquid in the liquid chamber. |
Conservation of Mass
The mass conservation in the block is
where
ρ0 is the constant liquid density. The block calculates this value from Preload pressure parameter.
Conservation of Momentum
Conservation of momentum is represented by the following equation.
where
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.
Examples
Extended Examples
Ports
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2020a