Building and Estimating Process Models Using System Identification Toolbox
This example shows how to build simple process models using System Identification Toolbox™. Techniques for creating these models and estimating their parameters using experimental data is described. This example requires Simulink®.
Introduction
This example illustrates how to build simple process models often used in process industry. Simple, low-order continuous-time transfer functions are usually employed to describe process behavior. Such models are described by IDPROC objects which represent the transfer function in a pole-zero-gain form.
Process models are of the basic type 'Static Gain + Time Constant + Time Delay'. They may be represented as:

or as an integrating process:
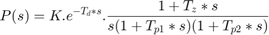
where the user can determine the number of real poles (0, 1, 2 or 3), as well as the presence of a zero in the numerator, the presence of an integrator term (1/s) and the presence of a time delay (Td). In addition, an underdamped (complex) pair of poles may replace the real poles.
Representation of Process Models Using IDPROC Objects
IDPROC objects define process models by using the letters P (for process model), D (for time delay), Z (for a zero) and I (for integrator). An integer will denote the number of poles. The models are generated by calling idproc with a character vector created using these letters.
For example:
idproc('P1') % transfer function with only one pole (no zeros or delay) idproc('P2DIZ') % model with 2 poles, delay integrator and delay idproc('P0ID') % model with no poles, but an integrator and a delay
ans =
Process model with transfer function:
Kp
G(s) = ----------
1+Tp1*s
Kp = NaN
Tp1 = NaN
Parameterization:
{'P1'}
Number of free coefficients: 2
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
ans =
Process model with transfer function:
1+Tz*s
G(s) = Kp * ------------------- * exp(-Td*s)
s(1+Tp1*s)(1+Tp2*s)
Kp = NaN
Tp1 = NaN
Tp2 = NaN
Td = NaN
Tz = NaN
Parameterization:
{'P2DIZ'}
Number of free coefficients: 5
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
ans =
Process model with transfer function:
Kp
G(s) = --- * exp(-Td*s)
s
Kp = NaN
Td = NaN
Parameterization:
{'P0DI'}
Number of free coefficients: 2
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
Creating an IDPROC Object (Using a Simulink Model as Example)
Consider the system described by the following Simulink model:
open_system('iddempr1') set_param('iddempr1/Random Number','seed','0')

The red part is the system, the blue part is the controller and the reference signal is a swept sinusoid (a chirp signal). The data sample time is set to 0.5 seconds. As observed, the system is a continuous-time transfer function, and can hence be described using model objects in System Identification Toolbox, such as idss, idpoly or idproc.
Let us describe the system using idpoly and idproc objects. Using idpoly object, the system may be described as:
m0 = idpoly(1,0.1,1,1,[1 0.5],'Ts',0,'InputDelay',1.57,'NoiseVariance',0.01);
The IDPOLY form used above is useful for describing transfer functions of arbitrary orders. Since the system we are considering here is quite simple (one pole and no zeros), and is continuous-time, we may use the simpler IDPROC object to capture its dynamics:
m0p = idproc('p1d','Kp',0.2,'Tp1',2,'Td',1.57) % one pole+delay, with initial values % for gain, pole and delay specified.
m0p =
Process model with transfer function:
Kp
G(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = 0.2
Tp1 = 2
Td = 1.57
Parameterization:
{'P1D'}
Number of free coefficients: 3
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
Estimating Parameters of IDPROC Models
Once a system is described by a model object, such as IDPROC, it may be used for estimation of its parameters using measurement data. As an example, we consider the problem of estimation of parameters of the Simulink model's system (red portion) using simulation data. We begin by acquiring data for estimation:
sim('iddempr1') dat1e = iddata(y,u,0.5); % The IDDATA object for storing measurement data
Let us look at the data:
plot(dat1e)

We can identify a process model using procest command, by providing the same structure information specified to create IDPROC models. For example, the 1-pole+delay model may be estimated by calling procest as follows:
m1 = procest(dat1e,'p1d'); % estimation of idproc model using data 'dat1e'. % Check the result of estimation: m1
m1 =
Process model with transfer function:
Kp
G(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = 0.20045
Tp1 = 2.0431
Td = 1.499
Parameterization:
{'P1D'}
Number of free coefficients: 3
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on time domain data "dat1e".
Fit to estimation data: 87.34%
FPE: 0.01069, MSE: 0.01062
To get information about uncertainties, use
present(m1)
m1 =
Process model with transfer function:
Kp
G(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = 0.20045 +/- 0.00077275
Tp1 = 2.0431 +/- 0.061216
Td = 1.499 +/- 0.040854
Parameterization:
{'P1D'}
Number of free coefficients: 3
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Termination condition: Near (local) minimum, (norm(g) < tol)..
Number of iterations: 4, Number of function evaluations: 9
Estimated using PROCEST on time domain data "dat1e".
Fit to estimation data: 87.34%
FPE: 0.01069, MSE: 0.01062
More information in model's "Report" property.
The model parameters, K, Tp1 and Td are now shown with one standard deviation uncertainty range.
Computing Time and Frequency Response of IDPROC Models
The model m1 estimated above is an IDPROC model object to which all of the toolbox's model commands can be applied:
step(m1,m0) %step response of models m1 (estimated) and m0 (actual) legend('m1 (estimated parameters)','m0 (known parameters)','location','northwest')

Bode response with confidence region corresponding to 3 standard deviations may be computed by doing:
h = bodeplot(m1,m0); showConfidence(h,3)

Similarly, the measurement data may be compared to the models outputs using compare as follows:
compare(dat1e,m0,m1)

Other operations such as sim, impulse, c2d are also available, just as they are for other model objects.
bdclose('iddempr1')
Accommodating the Effect of Intersample Behavior in Estimation
It may be important (at least for slow sampling) to consider the intersample behavior of the input data. To illustrate this, let us study the same system as before, but without the sample-and-hold circuit:
open_system('iddempr5')

Simulate this system with the same sample time:
sim('iddempr5') dat1f = iddata(y,u,0.5); % The IDDATA object for the simulated data
We estimate an IDPROC model using data1f while also imposing an upper bound on the allowable value delay. We will use 'lm' as search method and also choose to view the estimation progress.
m2_init = idproc('P1D'); m2_init.Structure.Td.Maximum = 2; opt = procestOptions('SearchMethod','lm','Display','on'); m2 = procest(dat1f,m2_init,opt); m2
m2 =
Process model with transfer function:
Kp
G(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = 0.20038
Tp1 = 2.01
Td = 1.31
Parameterization:
{'P1D'}
Number of free coefficients: 3
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on time domain data "dat1f".
Fit to estimation data: 87.26%
FPE: 0.01067, MSE: 0.01061

This model has a slightly less precise estimate of the delay than the previous one, m1:
[m0p.Td, m1.Td, m2.Td] step(m0,m1,m2) legend('m0 (actual)','m1 (estimated with ZOH)','m2 (estimated without ZOH)','location','southeast')
ans =
1.5700 1.4990 1.3100

However, by telling the estimation process that the intersample behavior is first-order-hold (an approximation to the true continuous) input, we do better:
dat1f.InterSample = 'foh';
m3 = procest(dat1f,m2_init,opt);

Compare the four models m0 (true) m1 (obtained from zoh input) m2 (obtained for continuous input, with zoh assumption) and m3 (obtained for the same input, but with foh assumption)
[m0p.Td, m1.Td, m2.Td, m3.Td] compare(dat1e,m0,m1,m2,m3)
ans =
1.5700 1.4990 1.3100 1.5570

step(m0,m1,m2,m3) legend('m0','m1','m2','m3') bdclose('iddempr5')

Modeling a System Operating in Closed Loop
Let us now consider a more complex process, with integration, that is operated in closed loop:
open_system('iddempr2')

The true system can be represented by:
m0 = idproc('P2ZDI','Kp',1,'Tp1',1,'Tp2',5,'Tz',3,'Td',2.2);
The process is controlled by a PD regulator with limited input amplitude and a zero order hold device. The sample time is 1 second.
set_param('iddempr2/Random Number','seed','0') sim('iddempr2') dat2 = iddata(y,u,1); % IDDATA object for estimation
Two different simulations are made, the first for estimation and the second one for validation purposes.
set_param('iddempr2/Random Number','seed','13') sim('iddempr2') dat2v = iddata(y,u,1); % IDDATA object for validation purpose
Let us look at the data (estimation and validation).
plot(dat2,dat2v) legend('dat2 (estimation)','dat2v (validation)')

Let us now perform estimation using dat2.
Warn = warning('off','Ident:estimation:underdampedIDPROC'); m2_init = idproc('P2ZDI'); m2_init.Structure.Td.Maximum = 5; m2_init.Structure.Tp1.Maximum = 2; opt = procestOptions('SearchMethod','lsqnonlin','Display','on'); opt.SearchOptions.MaxIterations = 100; m2 = procest(dat2, m2_init, opt)
m2 =
Process model with transfer function:
1+Tz*s
G(s) = Kp * ------------------- * exp(-Td*s)
s(1+Tp1*s)(1+Tp2*s)
Kp = 0.98412
Tp1 = 2
Tp2 = 1.4838
Td = 1.713
Tz = 0.027244
Parameterization:
{'P2DIZ'}
Number of free coefficients: 5
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on time domain data "dat2".
Fit to estimation data: 91.51%
FPE: 0.1128, MSE: 0.1092

compare(dat2v,m2,m0) % Gives very good agreement with data

bode(m2,m0)
legend({'m2 (est)','m0 (actual)'},'location','west')

impulse(m2,m0)
legend({'m2 (est)','m0 (actual)'})

Compare also with the parameters of the true system:
present(m2) [getpvec(m0), getpvec(m2)]
m2 =
Process model with transfer function:
1+Tz*s
G(s) = Kp * ------------------- * exp(-Td*s)
s(1+Tp1*s)(1+Tp2*s)
Kp = 0.98412 +/- 0.013672
Tp1 = 2 +/- 8.2231
Tp2 = 1.4838 +/- 10.193
Td = 1.713 +/- 63.703
Tz = 0.027244 +/- 65.516
Parameterization:
{'P2DIZ'}
Number of free coefficients: 5
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Termination condition: Change in cost was less than the specified tolerance..
Number of iterations: 3, Number of function evaluations: 4
Estimated using PROCEST on time domain data "dat2".
Fit to estimation data: 91.51%
FPE: 0.1128, MSE: 0.1092
More information in model's "Report" property.
ans =
1.0000 0.9841
1.0000 2.0000
5.0000 1.4838
2.2000 1.7130
3.0000 0.0272
A word of caution. Identification of several real time constants may sometimes be an ill-conditioned problem, especially if the data are collected in closed loop.
To illustrate this, let us estimate a model based on the validation data:
m2v = procest(dat2v, m2_init, opt) [getpvec(m0), getpvec(m2), getpvec(m2v)]
m2v =
Process model with transfer function:
1+Tz*s
G(s) = Kp * ------------------- * exp(-Td*s)
s(1+Tp1*s)(1+Tp2*s)
Kp = 0.95747
Tp1 = 1.999
Tp2 = 0.60819
Td = 2.314
Tz = 0.0010561
Parameterization:
{'P2DIZ'}
Number of free coefficients: 5
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on time domain data "dat2v".
Fit to estimation data: 90.65%
FPE: 0.1397, MSE: 0.1353
ans =
1.0000 0.9841 0.9575
1.0000 2.0000 1.9990
5.0000 1.4838 0.6082
2.2000 1.7130 2.3140
3.0000 0.0272 0.0011
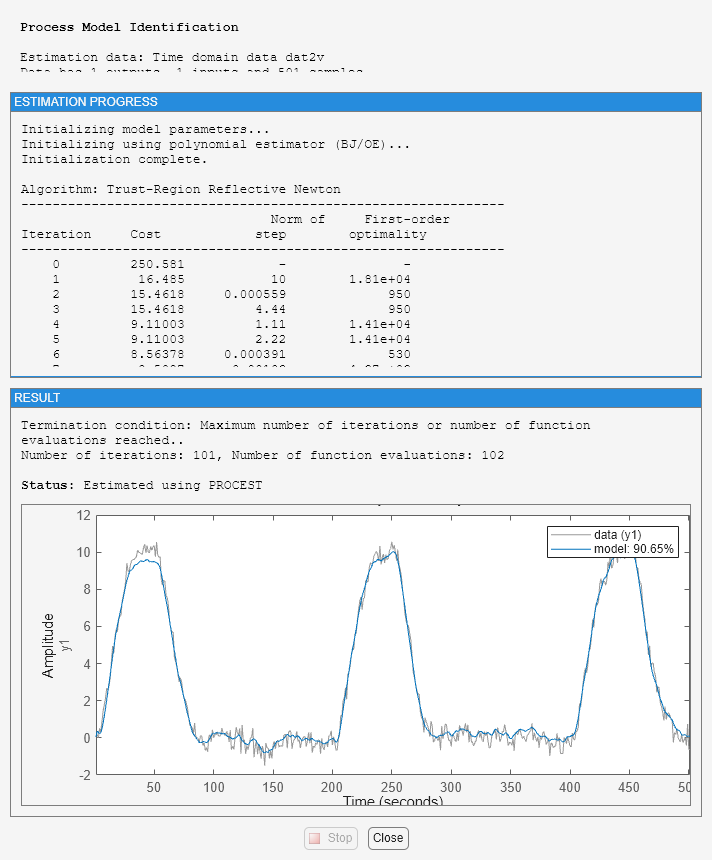
This model has much worse parameter values. On the other hand, it performs nearly identically to the true system m0 when tested on the other data set dat2:
compare(dat2,m0,m2,m2v)

Fixing Known Parameters During Estimation
Suppose we know from other sources that one time constant is 1:
m2v.Structure.Tp1.Value = 1; m2v.Structure.Tp1.Free = false;
We can fix this value, while estimating the other parameters:
m2v = procest(dat2v,m2v)
%
m2v =
Process model with transfer function:
1+Tz*s
G(s) = Kp * ------------------- * exp(-Td*s)
s(1+Tp1*s)(1+Tp2*s)
Kp = 1.0111
Tp1 = 1
Tp2 = 5.3014
Td = 2.195
Tz = 3.231
Parameterization:
{'P2DIZ'}
Number of free coefficients: 4
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on time domain data "dat2v".
Fit to estimation data: 92.05%
FPE: 0.09952, MSE: 0.09794

As observed, fixing Tp1 to its known value dramatically improves the estimates of the remaining parameters in model m2v.
This also indicates that simple approximation should do well on the data:
m1x_init = idproc('P2D'); % simpler structure (no zero, no integrator) m1x_init.Structure.Td.Maximum = 2; m1x = procest(dat2v, m1x_init) compare(dat2,m0,m2,m2v,m1x)
m1x =
Process model with transfer function:
Kp
G(s) = ----------------- * exp(-Td*s)
(1+Tp1*s)(1+Tp2*s)
Kp = -0.8956
Tp1 = 1.025e-06
Tp2 = 0.0047599
Td = 2
Parameterization:
{'P2D'}
Number of free coefficients: 4
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on time domain data "dat2v".
Fit to estimation data: -24.18%
FPE: 24.27, MSE: 23.89

Thus, the simpler model is able to estimate system output pretty well. However, m1x does not contain any integration, so the open loop long time range behavior will be quite different:
step(m0,m2,m2v,m1x) legend('m0','m2','m2v','m1x') bdclose('iddempr2') warning(Warn)
