Techniques for Visualizing Scalar Volume Data

What Is Scalar Volume Data?

Typical scalar volume data is composed of a 3-D array of data and three coordinate arrays of the same dimensions. The coordinate arrays specify the x-, y-, and z-coordinates for each data point.

The units of the coordinates depend on the type of data. For example, flow data might have coordinate units of inches and data units of psi.

A number of MATLAB^® functions are useful for visualizing scalar data:

• Slice planes provide a way to explore the distribution of data values within the volume by mapping values to colors. You can orient slice planes at arbitrary angles, as well as use nonplanar slices. (For illustrations of how to use slice planes, see slice, a volume slicing example, and slice planes used to show context.) You can specify the data used to color isosurfaces, enabling you to display different information in color and surface shape (see isocolors).

• Contour slices are contour plots drawn at specific coordinates within the volume. Contour plots enable you to see where in a given plane the data values are equal. See contourslice for an example.

• Isosurfaces are surfaces constructed by using points of equal value as the vertices of patch graphics objects.

Ways to Display MRI Data

• Changing the Data Format

• Displaying Images of MRI Data

• Displaying a 2-D Contour Slice

• Displaying 3-D Contour Slices

• Applying an Isosurface to the MRI Data

• Adding Isocaps Show Cut-Away Surface

• Defining the View

• Add Lighting

An example of scalar data includes magnetic resonance imaging (MRI) data. This data typically contains a number of slice planes taken through a volume, such as the human body. MATLAB includes an MRI data set that contains 27 image slices of a human head. This example illustrate the following techniques applied to MRI data:

• A series of 2-D images representing slices through the head

• 2-D and 3-D contour slices taken at arbitrary locations within the data

• An isosurface with isocaps showing a cross section of the interior

Changing the Data Format

The MRI data, D, is stored as a 128-by-128-by-1-by-27 array. The third array dimension is used typically for the image color data. However, since these are indexed images (a colormap, map, is also loaded) there is no information in the third dimension, which you can remove using the squeeze command. The result is a 128-by-128-by-27 array.

The first step is to load the data and transform the data array from 4-D to 3-D.

load mri
D = squeeze(D);

Displaying Images of MRI Data

To display one of the MRI images, use the image command:

• Create a new figure that uses the MRI colormap, which is loaded with the data:

• Index into the data array to obtain the data for the eighth image.

• Adjust axis scaling.

figure
colormap(map)
image_num = 8;
image(D(:,:,image_num))
axis image

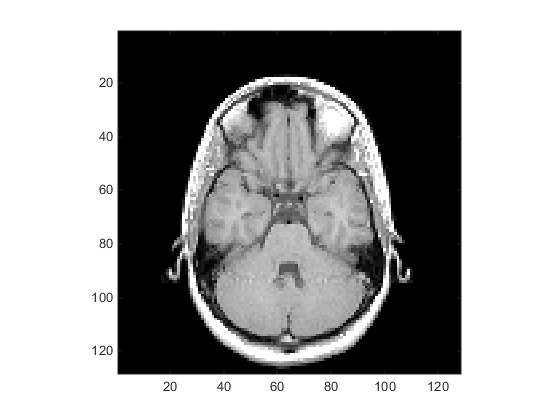
Save the x- and y-axis limits for use in the next part of the example:

x = xlim;
y = ylim;

Displaying a 2-D Contour Slice

Visualize MRI data as a volume data because it is a collection of slices taken progressively through the 3-D object. Use contourslice to display a contour plot of a volume slice. Create a contour plot with the same orientation and size as the image created in the first part of this example:

• Adjust the y-axis direction (axis).

• Set the limits (xlim, ylim).

• Set the data aspect ratio (daspect).

To improve the visibility of details, this contour plot uses the jet colormap. The brighten function reduces the brightness of the color values.

cm = brighten(jet(length(map)),-.5);
figure
colormap(cm)
contourslice(D,[],[],image_num)
axis ij
xlim(x)
ylim(y)
daspect([1,1,1])

Displaying 3-D Contour Slices

Unlike images, which are 2-D objects, contour slices are 3-D objects that you can display in any orientation. For example, you can display four contour slices in a 3-D view.

figure
colormap(cm)
contourslice(D,[],[],[1,12,19,27],8);
view(3);
axis tight

Applying an Isosurface to the MRI Data

You can use isosurfaces to display the overall structure of a volume. When combined with isocaps, this technique can reveal information about data on the interior of the isosurface.

First, smooth the data with smooth3; then use isosurface to calculate the isodata. Use patch to display this data in a figure that uses the original gray scale color map for the isocaps.

figure
colormap(map)
Ds = smooth3(D);
hiso = patch(isosurface(Ds,5),...
   'FaceColor',[1,.75,.65],...
   'EdgeColor','none');
   isonormals(Ds,hiso)

The isonormals function to renders the isosurface using vertex normals obtained from the smoothed data, improving the quality of the isosurface. The isosurface uses a single color to represent its isovalue.

Adding Isocaps Show Cut-Away Surface

Use isocaps to calculate the data for another patch that is displayed at the same isovalue (5) as the isosurface. Use the unsmoothed data (D) to show details of the interior. You can see this as the sliced-away top of the head. The lower isocap is not visible in the final view.

hcap = patch(isocaps(D,5),...
   'FaceColor','interp',...
   'EdgeColor','none');

Defining the View

Define the view and set the aspect ratio (view, axis, daspect).

view(35,30) 
axis tight 
daspect([1,1,.4])

Add Lighting

Add lighting and recalculate the surface normals based on the gradient of the volume data, which produces smoother lighting (camlight, lighting, isonormals). Increase the AmbientStrength property of the isocap to brighten the coloring without affecting the isosurface. Set the SpecularColorReflectance of the isosurface to make the color of the specular reflected light closer to the color of the isosurface; then set the SpecularExponent to reduce the size of the specular spot.

lightangle(45,30);
lighting gouraud
hcap.AmbientStrength = 0.6;
hiso.SpecularColorReflectance = 0;
hiso.SpecularExponent = 50;

Here is a visualization of the MRI data that combines an isocap with an isosurface.

The isocaps use interpolated face coloring, which means the figure colormap determines the coloring of the patch. This example uses the colormap supplied with the data.

To display isocaps at other data values, try changing the isosurface value or use the subvolume command. See the isocaps and subvolume reference pages for examples.