Solve a Finite Set MPC Problem in Simulink

This example shows how to solve, using Simulink®, an MPC problem in which some manipulated variables belong to a finite (discrete) set.

Create a Plant Model

Fix the random generator seed for reproducibility.

rng(0);

Create a discrete-time strictly proper plant with 4 states, two inputs and one output.

plant = drss(4,1,2);
plant.D = 0;

Increase the control authority of the first input, to better illustrate its control contribution.

plant.B(:,1)=plant.B(:,1)*2;

Design the MPC Controller

Create an MPC controller with one second sampling time, 20 steps prediction horizon and 5 steps control horizon.

mpcobj = mpc(plant,0.1,20,5);

-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000.
-->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000.
-->"Weights.OutputVariables" is empty. Assuming default 1.00000.

Specify the first manipulated variable as belonging to a set of seven possible values. Note that you could also specify it as an integer using the instruction mpcobj.MV(1).Type = 'integer'; in which case the first manipulated variable will be constrained to be an integer.

mpcobj.MV(1).Type = [-1 -0.7 -0.3 0 0.2 0.5 1];

Use rate limits to enforce maximum increment and decrement values for the first manipulated variable.

mpcobj.MV(1).RateMin = -0.5;
mpcobj.MV(1).RateMax = 0.5;

Set limits on the second manipulated variable, whose default type (continuous) has not been changed.

mpcobj.MV(2).Min = -2;
mpcobj.MV(2).Max = 2;

Control the Plant Model in Simulink

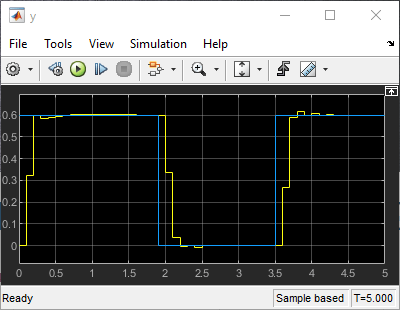
Create an output reference signal equal to zero from steps 20 to 35 and equal to 0.6 before and after.

r = ones(1,50)*0.6;
r(20:35) = 0;

Create a Simulink closed loop simulation using the MPC Controller block, with the mpcobj object passed as a parameter, to control the double integrator plant. For this example, open the pre-existing Simulink model dcsdemo.slxc.

open('dcsdemo.slx')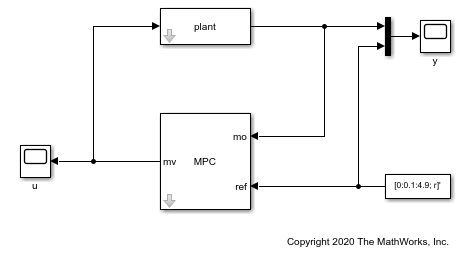

You can now run the model by clicking Run or by using the MATLAB® command sim.

sim('dcsdemo.slx')

-->No sample time in plant model. Assuming controller's sample time of 0.1.
-->Assuming output disturbance added to measured output #1 is integrated white noise.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

ans = 
  Simulink.SimulationOutput:
                   tout: [51x1 double] 

     SimulationMetadata: [1x1 Simulink.SimulationMetadata] 
           ErrorMessage: [0x0 char] 

After the simulation, the plots of the two scopes show that the manipulated variable does not exceed the limit and the plant output tracks the reference signal after approximately half a second.