Adjust Solve Parameters in the PDE Modeler App
To specify parameters for solving a PDE, select Parameters from the
Solve menu. The set of solve parameters differs depending on
the type of PDE. After you adjust the parameters, solve the PDE by selecting
Solve PDE from the Solve menu or
by clicking the ![]() button.
button.
Elliptic Equations

By default, no specific solve parameters are used, and the elliptic
PDEs are solved using the basic elliptic solver assempde.
Optionally, the adaptive mesh generator and solver adaptmesh can
be used. For the adaptive mode, the following parameters are available:
Adaptive mode. Toggle the adaptive mode on/off.
Maximum number of triangles. The maximum number of new triangles allowed (can be set to
Inf). A default value is calculated based on the current mesh.Maximum number of refinements. The maximum number of successive refinements attempted.
Triangle selection method. There are two triangle selection methods, described below. You can also supply your own function.
Worst triangles. This method picks all triangles that are worse than a fraction of the value of the worst triangle (default: 0.5).
Relative tolerance. This method picks triangles using a relative tolerance criterion (default: 1E-3).
User-defined function. Enter the name of a user-defined triangle selection method. See Poisson's Equation with Point Source and Adaptive Mesh Refinement for an example of a user-defined triangle selection method.
Function parameter. The function parameter allows fine-tuning of the triangle selection methods. For the worst triangle method (
pdeadworst), it is the fraction of the worst value that is used to determine which triangles to refine. For the relative tolerance method, it is a tolerance parameter that controls how well the solution fits the PDE.Refinement method. Can be
regularorlongest. See Specify Mesh Parameters in the PDE Modeler App.
If the problem is nonlinear, i.e., parameters in the PDE are
directly dependent on the solution u, a nonlinear
solver must be used. The following parameters are used:
Use nonlinear solver. Toggle the nonlinear solver on/off.
Nonlinear tolerance. Tolerance parameter for the nonlinear solver.
Initial solution. An initial guess. Can be a constant or a function of x and y given as a MATLAB® expression that can be evaluated on the nodes of the current mesh.
Examples:
1, andexp(x.*y). Optional parameter, defaults to zero.Jacobian. Jacobian approximation method:
fixed(the default), a fixed point iteration,lumped, a “lumped” (diagonal) approximation, orfull, the full Jacobian.Norm. The type of norm used for computing the residual. Enter as
energyfor an energy norm, or as a real scalar p to give the lp norm. The default isInf, the infinity (maximum) norm.Note
The adaptive mode and the nonlinear solver can be used together.
Parabolic Equations
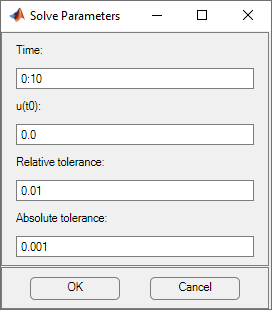
The solve parameters for the parabolic PDEs are:
Time. A MATLAB vector of times at which a solution to the parabolic PDE should be generated. The relevant time span is dependent on the dynamics of the problem.
Examples:
0:10, andlogspace(-2,0,20)u(t0). The initial value u(t0) for the parabolic PDE problem The initial value can be a constant or a column vector of values on the nodes of the current mesh.
Relative tolerance. Relative tolerance parameter for the ODE solver that is used for solving the time-dependent part of the parabolic PDE problem.
Absolute tolerance. Absolute tolerance parameter for the ODE solver that is used for solving the time-dependent part of the parabolic PDE problem.
Hyperbolic Equations
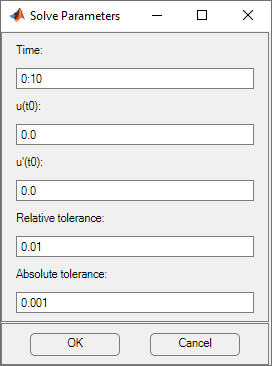
The solve parameters for the hyperbolic PDEs are:
Time. A MATLAB vector of times at which a solution to the hyperbolic PDE should be generated. The relevant time span is dependent on the dynamics of the problem.
Examples:
0:10, andlogspace(-2,0,20).u(t0). The initial value u(t0) for the hyperbolic PDE problem. The initial value can be a constant or a column vector of values on the nodes of the current mesh.
u'(t0). The initial value (t0) for the hyperbolic PDE problem. You can use the same formats as for u(t0).
Relative tolerance. Relative tolerance parameter for the ODE solver that is used for solving the time-dependent part of the hyperbolic PDE problem.
Absolute tolerance. Absolute tolerance parameter for the ODE solver that is used for solving the time-dependent part of the hyperbolic PDE problem.
Eigenvalue Equations
For the eigenvalue PDE, the only solve parameter is the Eigenvalue
search range, a two-element vector, defining an interval
on the real axis as a search range for the eigenvalues. The left side
can be -Inf.
Examples: [0 100], [-Inf 50]

Nonlinear Equations
Before solving a nonlinear elliptic PDE in the PDE Modeler app, select SolveParameters. Then select Use nonlinear solver and click OK.
