diffbfweights
Syntax
Description
wts = diffbfweights(nelem,elemspacing)nelem is the number of elements in the array and
elemspacing is the distance between array elements. Differential
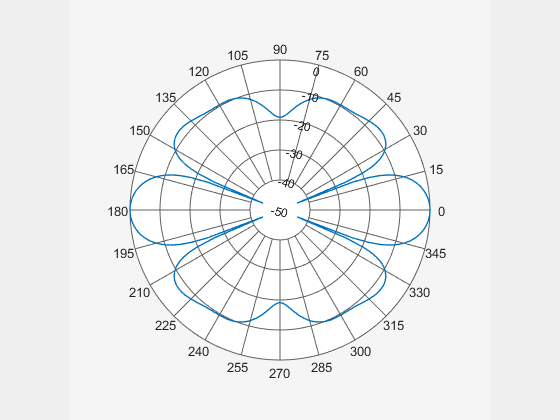
weights can achieve frequency invariant beam patterns and are often used in microphone
arrays.
wts = diffbfweights(nelem,elemspacing,ArrayGeometry='ULA')
wts = diffbfweights(nelem,elemspacing,angc,ArrayGeometry=ag)angc at which the array response is null. When
ag equals 'ULA', elemspacing refers to the
distance between array elements. When ag equals 'UCA',
elemspacing refers to the array radius.
Examples
Input Arguments
Output Arguments
References
[1] Benesty, Jacob, et al. Fundamentals of Differential Beamforming. Springer Singapore, 2016. DOI.org (Crossref), https://doi.org/10.1007/978-981-10-1046-0.
[2] Benesty, Jacob, and J. Chen. Study and Design of Differential Microphone Arrays. Springer, 2013.
[3] Jingdong Chen, Jacob Benesty, and Chao Pan, "On the design and implementation of linear differential microphone arrays", The Journal of the Acoustical Society of America, Vol 136, pp 3097, 2014.
[4] Jilu Jin, Gongping Huang, Xuehan Wang, Jingdong Chen, Jacob Benesty, and Israel Cohen, "Steering Study of Linear Differential Microphone Arrays", IEEE/ACM Transactions on Audio, Speech, and Language Processing, Vol 29, pp 158, 2020
[5] Jacob Benesty, Jingdong Chen, and Israel Cohen, Design of Circular Differential Microphone Arrays, Springer 2015.
[6] Gongping Huang, Israel Cohen, Jingdong Chen, and Jacob Benesty, "Continuously steerable differential beamformers with null constraints for circular microphone arrays", The Journal of the Acoustical Society of America, Vol 148, pp 1248, 2020.
Version History
Introduced in R2022a
See Also
steervec | arrayfactor | polarpattern | phased.SteeringVector