clutterSurfaceRCS
Syntax
Description
Examples
Calculate the radar cross section of a clutter patch and estimate the clutter-to-noise ratio at the receiver. Assume that the patch is 1000 meters away from the radar system and the azimuth and elevation beamwidths are 1 degree and 3 degrees, respectively. Also assume that the grazing angle is 20 degrees, the pulse width is 10 microseconds, and the radar is operated at a wavelength of 1 cm with a peak power of 5 kw.
rng = 1000; bwAz = 1; bwEl = 3; graz = 20; tau = 10e-6; lambda = 0.01; ppow = 5000;
Calculate the NRCS.
nrcs = landreflectivity('Mountains',graz)nrcs = 0.1082
Calculate clutter RCS using the calculated NRCS.
rcs = clutterSurfaceRCS(nrcs,rng,bwAz,bwEl,graz,tau)
rcs = 288.9855
Calculate clutter-to-noise ratio using the calculated RCS.
cnr = radareqsnr(lambda,rng,ppow,tau,'rcs',rcs)cnr = 62.5974
Since R2025a
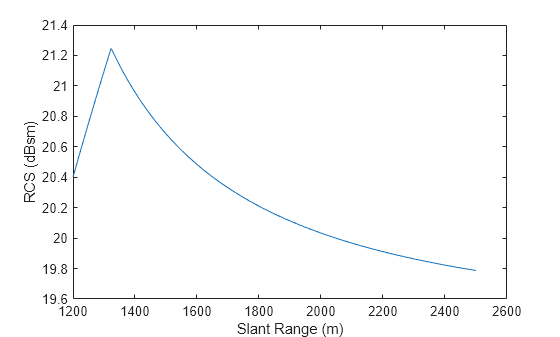
This example shows the RCS of the illuminated clutter region calculated as a function of slant range.
First, calculate the corresponding grazing angles for a set of ranges between 1.1 and 3 km. The radar is located at an altitude of 1 km and operates at a frequency of 1 GHz. It has a 5 degree symmetric beamwidth and a pulse width corresponding to 100 meters.
alt = 1e3;
freq = 1e9;
beamwidth = 5;
tau = 2*100/physconst('lightspeed');
slantRange = linspace(1.2e3,2.5e3,1e3).';
graze = asind(alt./slantRange);Next, calculate surface NRCS using the Barton constant-gamma reflectivity model for farmland.
nrcs = landreflectivity('Farm',graze,freq);Finally, calculate RCS and plot in dBsm. The inflection point around 1.3 km is caused by switching from the beam-limited clutter calculation to the pulse-limited clutter calculation.
rcs = clutterSurfaceRCS(nrcs,slantRange,beamwidth,beamwidth,graze,tau); plot(slantRange,10*log10(rcs)) xlabel('Slant Range (m)') ylabel('RCS (dBsm)')
Input Arguments
Normalized radar cross section (NRCS) of a clutter patch specified as either a
nonnegative scalar or an M-length vector of nonnegative values. Units
are dimensionless but often expressed as m²/m². Each entry in nrcs
corresponds to a slant range specified in range. The NRCS provides
a measure of the reflectivity of a surface per unit area and is also referred to as σ0, the backscatter coefficient or reflectivity. NRCS can be determined
from built-in surface models that are valid for pre-defined frequencies and grazing
angles using landreflectivity and seareflectivity.
Example: nrcs = 1
Data Types: double
Clutter patch slant range, specified as either a nonnegative scalar or an
M-length vector of nonnegative values in units of meters. Each
entry in range corresponds to a an entry in
nrcs.
The Beam-Illuminated Approximation clutter approximation is valid at close range whereas the Pulse-Illuminated Approximation clutter approximation is valid at long range. See Beam-Limited and Pulse-Limited Clutter. (since R2025a)
Example: 1000
Data Types: double
Azimuth beamwidth of the radar, specified as a positive scalar or a 1-by-2 vector in
units of degrees. Use with the elevation argument.
When the transmit and receive beamwidths are the same, specify
azimuthas a positive scalar.When the transmit and receive azimuth beamwidths are not the same, specify
azimuthas a 1-by-2 positive vector[azimuth_Tx,azimuth_Rx], where the first element is the transmit azimuth beamwidth in degrees and the second element is the receive azimuth beamwidth.
clutterSurfaceRCS uses these two beamwidths to create an effective
azimuth beamwidth. See Effective Beamwidth.
Example: 1
Data Types: double
Elevation beamwidth of the radar, specified as a positive scalar or a 1-by-2 vector
in units of degrees. Use with the azimuth argument.
When the transmit and receive beamwidths are the same, specify
elevationas a positive scalar.When the transmit and receive elevation beamwidths are not the same, specify
elevationas a 1-by-2 positive vector[elevation_Tx,elevation_Rx], where the first element is the transmit elevation beamwidth and the second element is the receive elevation beamwidth.
clutterSurfaceRCS uses these two beamwidths to create an effective
elevation beamwidth. See Effective Beamwidth.
Example: 3
Data Types: double
Grazing angles of the clutter patches relative to the radar, specified as a
nonnegative scalar or an M-length row vector of nonnegative values.
Units are in degrees. Each entry in graz corresponds to a NRCS
value specified in nrcs. See grazingang.
Data Types: double
Pulse width of the transmitted signal, specified as a nonnegative scalar in units of seconds.
The pulse width is used to calculated the region illuminated by the radar for the Pulse-Illuminated Approximation approximation. (since R2025a)
Example: 10e-6
Data Types: double
Propagation speed, specified as a positive scalar in units of meters per second.
Data Types: double
Beamshape loss, specified as a nonnegative scalar in decibels. The beamshape loss accounts for the reduced two-way antenna gain of off-axis scatterers.
Use this property when the elevation beamwidth (elevation) for
the transmitter and receiver are not the same.
Example: Lp = 0
Data Types: double
Output Arguments
The radar cross section of each surface clutter patch, returned as an scalar or M-length vector, in units of square meters.
More About
The effective beamwidth is used for the effective azimuth θazimutheff and effective elevation θelevationeff calculation when the transmitter and receiver beamwidths are not equal.
at is the azimuth transmitter elevation beamwidth in degrees.
ar is the azimuth receiver elevation beamwidth in degrees.
et is the elevation transmitter elevation beamwidth in degrees.
er is the elevation receiver elevation beamwidth in degrees.
At close range relevant to broadside pointing, clutterSurfaceRCS
approximates the region illuminated by the radar as beam-illuminated. The extent of the
beam-illuminated region depends on the radar beamwidth and the distance to the target. For a
scenario geometry in which the radar beam is pointed downward so that it intersects a flat
surface, the distance to the ground, or slant range, is a function of the radar altitude and
grazing angle. Assume that the radar beam is conical with an elliptical beam
footprint. The region illuminated by the beam is an ellipse defined by the intersection of
the conical beam with the surface.
The area of the beam-illuminated region is approximated as a rectangle. The width, or extent in the azimuthal direction, Wbeam, is taken as the arc length of the azimuth cut of the beam at the slant range, R. That is, , where θaz is the azimuth angle. This width is greater than the actual average width of the beam, but smaller than the maximum width of the beam. The length, or extent in the elevation direction, Lbeam, is taken as the arc length of the elevation cut of the beam, modulated by the sine of the grazing angle, Ψ. That is, , where θel is the elevation angle. This expression is applicable for broadside pointing and is most accurate for high grazing angles or short ranges. It may underestimate the true length of the region in other cases. The area of the beam-illuminated region, Abeam, is defined as Abeam = Wbeam × Lbeam.
At long range, clutterSurfaceRCS approximates the region
Illuminated by the radar as pulse-illuminated. The extent of the surface in the range
direction that falls within one range bin is where is the pulse width, (tau), given a propagation speed of c, and
Ψ is the grazing angle. The figure below illustrates that the pulse
width in the slant plane needs to be increased by a factor of to get the length of the pulse-illuminated region in the ground plane. The
area of the pulse-illuminated region, Apulse, is
defined as Apulse =
Wbeam*
Lpulse.
If the length of the pulse along the ground, Lpulse, is greater than the length of the beam-illuminated region, Lbeam, then the illuminated region within a range cell has area Abeam. This is known as beam-limited clutter and tends to occur with high grazing angles. If Lpulse is less than Lbeam, the area of the illuminated region is Apulse. This is known as pulse-limited clutter and tends to occur for low grazing angles. The figure below shows these two regions as a function of grazing angle and pulse width for a scenario with a 1 km altitude and 5 degree azimuth and elevation beamwidths. Also see RCS of Beam-Illuminated and Pulse-Illuminated Clutter, which shows RCS as a function of slant range to highlight the inflection point that results from transitioning from a beam-limited to a pulse-limited clutter calculation.
References
[1] Barton, David K. Radar Equations for Modern Radar. Norwood, MA: Artech House, 2013.
[2] Long, Maurice W. Radar Reflectivity of Land and Sea. Boston: Artech House, 2001.
[3] Nathanson, Fred E., J. Patrick Reilly, and Marvin N. Cohen. Radar Design Principles. Mendham, NJ: SciTech Publishing, 1999.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Version History
Introduced in R2021a
See Also
landreflectivity | seareflectivity | radareqsnr | surfacegamma | grazingang
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)