loopsens
Sensitivity functions of plant-controller feedback loop
Syntax
Description
loops = loopsens(P,C)C in negative feedback with the plant
P. To compute the sensitivity functions for the system with positive
feedback, use loopsens(P,-C).
Examples
Consider PI controller for a dominantly first-order plant, with the closed-loop bandwidth of 2.5 rads/sec. Since the problem is SISO, all gains are the same at input and output.
gamma = 2; tau = 1.5; taufast = 0.1; P = tf(gamma,[tau 1])*tf(1,[taufast 1]); tauclp = 0.4; xiclp = 0.8; wnclp = 1/(tauclp*xiclp); KP = (2*xiclp*wnclp*tau - 1)/gamma; KI = wnclp^2*tau/gamma; C = tf([KP KI],[1 0]);
Form the closed-loop (and open-loop) systems with loopsens, and plot Bode plots of the sensitivity functions at the plant input.
loops = loopsens(P,C); bode(loops.Si,'r',loops.Ti,'b',loops.Li,'g') legend('Sensitivity','Complementary Sensitivity','Loop Transfer')

Finally, compare the open-loop plant gain to the closed-loop value of PSi.
bodemag(P,'r',loops.PSi,'b') legend('Plant','Sensitivity*Plant')

Consider an integral controller for a constant-gain, 2-input, 2-output plant. For purposes of illustration, the controller is designed via inversion, with different bandwidths in each rotated channel.
P = ss([2 3;-1 1]); BW = diag([2 5]); [U,S,V] = svd(P.d); % get SVD of Plant Gain Csvd = V*inv(S)*BW*tf(1,[1 0])*U'; % inversion based on SVD loops = loopsens(P,Csvd); bode(loops.So,'g',loops.To,'r',logspace(-1,3,120)) title('Output Sensitivity (green), Output Complementary Sensitivity (red)');

Input Arguments
Plant, specified as a dynamic system model, control design block, or static gain
matrix. P can be SISO or MIMO, as long as P*C
has the same number of inputs and outputs.
P can be continuous time or discrete time. If
P is a generalized model (such as genss or
uss) then loopsens uses the current or
nominal value of all control design blocks in P.
Controller, specified as a dynamic system model, control design block, or static
gain matrix. The controller can be any of the model types that P
can be, as long as P*C has the same number of inputs and outputs.
loopsens computes the sensitivity
functions assuming a negative-feedback closed-loop system. To compute the
sensitivity functions for the system with positive feedback, use
loopsens(P,-C).
The loopsens command assumes one-degree-of-freedom control
architecture. If you have a two-degree-of-freedom architecture, then construct
C to include only the compensator in the feedback path, not any
reference channels.
Output Arguments
Sensitivity functions of the feedback loop
feedback(P,C), returned in a structure having the fields shown in
the table below. The sensitivity functions are returned as state-space
(ss) models of the same I/O dimensions as C*P. If
P or C is a frequency-response-data model,
then the sensitivity functions are frd models.
Field | Description |
|---|---|
Si | Input-to-plant sensitivity function. |
Ti | Input-to-plant complementary sensitivity function. |
Li | Input-to-plant loop transfer function. |
So | Output-to-plant sensitivity function. |
To | Output-to-plant complementary sensitivity function. |
Lo | Output-to-plant loop transfer function. |
PSi | Plant times input-to-plant sensitivity function. |
CSo | Compensator times output-to-plant sensitivity function. |
Poles | Poles of the closed loop |
Stable | 1 if nominal closed loop is stable, 0 otherwise. If either
|
More About
The closed-loop interconnection structure shown below defines the
input/output sensitivity, complementary sensitivity, and loop transfer functions. The
structure includes multivariable systems in which P and
C are MIMO systems.
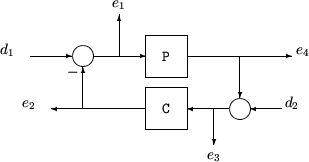
The following table gives the values of the input and output sensitivity functions for this control structure.
Description | Equation |
|---|---|
Input sensitivity Si (closed-loop transfer function from d1 to e1) | Si = (I + CP)–1 |
Input complementary sensitivity Ti (closed-loop transfer function from d1 to e2) | Ti = CP(I + CP)–1 |
Output sensitivity So (closed-loop transfer function from d2 to e3) | So = (I + PC)–1 |
Output complementary sensitivity To (closed-loop transfer function from d2 to e4) | To = PC(I + PC)–1 |
Input loop transfer function Li | Li = CP |
Output loop transfer function Lo | Lo = PC |
Version History
Introduced before R2006a
See Also
diskmargin | robstab | wcgain | wcdiskmargin
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)