Uncertain Complex Parameters and Matrices
Uncertain Complex Parameters
The ucomplex element is the Control Design Block that represents an uncertain
complex number. The value of an uncertain complex number lies in a disc, centered at
NominalValue, with radius specified by the Radius
property of the ucomplex element. The size of the disc can also be
specified by Percentage, which means the radius is derived from the
absolute value of the NominalValue. The properties of ucomplex objects are
|
Properties |
Meaning |
Class |
|---|---|---|
|
|
Internal Name |
|
|
|
Nominal value of element |
|
|
|
|
|
|
|
Radius of disk |
|
|
|
Additive variation (percent of |
|
|
|
|
|
Create Uncertain Complex Parameter
The simplest construction requires only a name and nominal value.
a = ucomplex('a',2-j)Uncertain complex parameter "a" with nominal value 2-1i and radius 1. Block Properties
Displaying the properties shows that the default Mode is Radius, and the default radius is 1.
get(a)
NominalValue: 2.0000 - 1.0000i
Mode: 'Radius'
Radius: 1
Percentage: 44.7214
AutoSimplify: 'basic'
Name: 'a'
Sample the uncertain complex parameter at 400 values and plot the samples in the complex plane. The plot shows that the samples all fall within a disc of radius 1, centered in the complex plane at the value 2 – j.
asample = usample(a,400);
plot(asample(:),'o');
xlim([-0.5 4.5]);
ylim([-3 1]);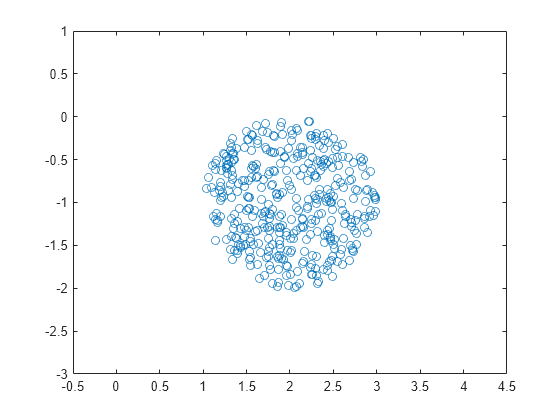
Uncertain Complex Matrices
The uncertain complex matrix class, ucomplexm, represents the set of matrices given by the formula
N + WLΔWR
where N, WL, and
WR are known matrices, and Δ is any complex
matrix with . All properties of a ucomplexm are can be accessed with get and
set. The properties are
|
Properties |
Meaning |
Class |
|---|---|---|
|
|
Internal Name |
|
|
|
Nominal value of element |
|
|
|
Left weight |
|
|
|
Right weight |
|
|
|
|
|
Uncertain Complex Matrix and Weighting Matrices
Create a 4-by-3 uncertain complex matrix (ucomplexm), and view its properties. The simplest construction requires only a name and nominal value.
m = ucomplexm('m',[1 2 3; 4 5 6; 7 8 9; 10 11 12])Uncertain complex matrix "m" with 4 rows and 3 columns. Block Properties
get(m)
NominalValue: [4×3 double]
WL: [4×4 double]
WR: [3×3 double]
AutoSimplify: 'basic'
Name: 'm'
The nominal value is the matrix you supply to ucomplexm.
mnom = m.NominalValue
mnom = 4×3
1 2 3
4 5 6
7 8 9
10 11 12
By default, the weighting matrices are the identity. For example, examine the left weighting.
m.WL
ans = 4×4
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Sample the uncertain matrix, and compare to the nominal value. Note the element-by-element sizes of the difference are roughly equal, indicative of the identity weighting matrices.
msamp = usample(m); diff = abs(msamp-mnom)
diff = 4×3
0.3309 0.0917 0.2881
0.2421 0.3449 0.3917
0.2855 0.2186 0.2915
0.3260 0.2753 0.3816
Change the left and right weighting matrices, making the uncertainty larger as you move down the rows, and across the columns.
m.WL = diag([0.2 0.4 0.8 1.6]); m.WR = diag([0.1 1 4]);
Sample the uncertain matrix again, and compare to the nominal value. Note the element-by-element sizes of the difference, and the general trend that the smallest differences are near the (1,1) element, and the largest differences are near the (4,3) element, consistent with the trend in the diagonal weighting matrices.
msamp = usample(m); diff = abs(msamp-mnom)
diff = 4×3
0.0048 0.0526 0.2735
0.0154 0.1012 0.4898
0.0288 0.3334 0.8555
0.0201 0.4632 1.3783