pulseperiod
Period of bilevel pulse
Syntax
Description
p = pulseperiod(x)x. To determine the transitions for each pulse, the
pulseperiod function estimates the state levels of the input waveform by a
histogram method and identifies all regions which cross the upper-state boundary of the low
state and the lower-state boundary of the high state.
[
returns the mid-reference level instants p,initcross,finalcross]
= pulseperiod(___)finalcross of the final transition
of each pulse. You can specify an input combination from any of the previous syntaxes.
[
returns the mid-reference level instants p,initcross,finalcross,nextcross]
= pulseperiod(___)nextcross of the next detected
transition after each pulse.
[
returns the mid-reference level p,initcross,finalcross,nextcross,midlev]
= pulseperiod(___)midlev.
[
returns the pulse periods with additional options specified by one or more name-value
arguments.p,initcross,finalcross,nextcross,midlev]
= pulseperiod(___,Name,Value)
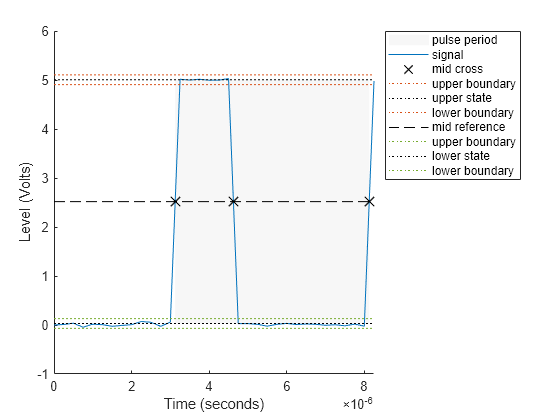
pulseperiod(___) plots the signal and darkens every other
identified pulse. The function marks the location of the mid crossings and their associated
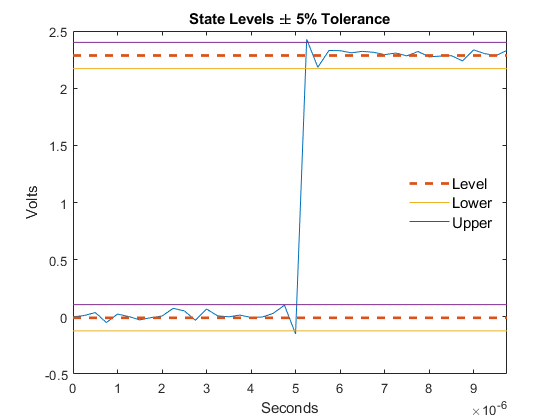
reference level. The function also plots the state levels and their associated lower and upper
boundaries. You can adjust the boundaries using the 'Tolerance' name-value
argument.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] IEEE® Standard on Transitions, Pulses, and Related Waveforms, IEEE Standard 181, 2003.
Extended Capabilities
Version History
Introduced in R2012a