Learn Pre-Emphasis Filter Using Deep Learning

This example shows how to use a convolutional deep network to learn a pre-emphasis filter for speech recognition. The example uses a learnable short-time Fourier transform (STFT) layer to obtain a time-frequency representation suitable for use with 2-D convolutional layers. The use of a learnable STFT enables a gradient-based optimization of the pre-emphasis filter weights.

Data

Clone or download the Free Spoken Digit Dataset (FSDD), available at https://github.com/Jakobovski/free-spoken-digit-dataset. FSDD is an open data set, which means that it can grow over time. This example uses the version committed on 08/20/2020 which consists of 3000 recordings of the English digits 0 through 9 obtained from six speakers. The data is sampled at 8000 Hz.

This example assumes that you have downloaded the data into the folder corresponding to the value of tempdir in MATLAB. If you use a different folder, substitute that folder name for tempdir in the following code. Use audioDatastore to manage data access and ensure random division of data into training and test sets.

pathToRecordingsFolder = fullfile(tempdir,'free-spoken-digit-dataset','recordings');
ads = audioDatastore(pathToRecordingsFolder);

Use the filenames2labels function to obtain a categorical vector of labels from the FSDD files. Display the count of each label in the data set.

lbls = filenames2labels(ads,ExtractBefore="_");
ads.Labels = lbls;
countlabels(lbls)

ans=10×3 table
    Label    Count    Percent
    _____    _____    _______

      0       300       10   
      1       300       10   
      2       300       10   
      3       300       10   
      4       300       10   
      5       300       10   
      6       300       10   
      7       300       10   
      8       300       10   
      9       300       10   

Split the FSDD into training and test sets maintaining equal class proportions in each subset. For reproducible results, set the random number generator to its default value. Eighty percent, or 2400 recordings, are used for training. The remaining 600 recordings, 20% of the total, are held out for testing. Shuffle the files in the datastore once before creating the training and test sets.

rng default;
ads = shuffle(ads);
[adsTrain,adsTest] = splitEachLabel(ads,0.8,0.2);

The recordings in FSDD are not equal in length. Use a transform so that each read from the datastore is padded or truncated to 8192 samples. The data are additionally cast to single-precision and a z-score normalization is applied.

transTrain = transform(adsTrain,@(x,info)helperReadData(x,info),'IncludeInfo',true);
transTest = transform(adsTest,@(x,info)helperReadData(x,info),'IncludeInfo',true);

Deep Convolutional Neural Network (DCNN) Architecture

This example uses a custom training loop with the following deep convolutional network.

numF = 12;
dropoutProb = 0.2;
layers = [
    sequenceInputLayer(1,'Name','input','MinLength',8192,...
         'Normalization',"none")

    convolution1dLayer(5,1,"name","pre-emphasis-filter",...
    "WeightsInitializer",@(sz)kronDelta(sz),"BiasLearnRateFactor",0)  

    stftLayer('Window',hamming(1280),'OverlapLength',900,...
    'Name','STFT') 
    
    convolution2dLayer(5,numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,2*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,2*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')
    
    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')
   
    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    maxPooling2dLayer(3,'Stride',2,'Padding','same')

    convolution2dLayer(3,4*numF,'Padding','same')
    batchNormalizationLayer
    reluLayer

    dropoutLayer(dropoutProb)
    globalAveragePooling2dLayer
    fullyConnectedLayer(numel(categories(ads.Labels)))
    softmaxLayer    
    ];
dlnet = dlnetwork(layers);

The sequence input layer is followed by a 1-D convolution layer consisting of a single filter with 5 coefficients. This is a finite impulse response filter. Convolutional layers in deep learning networks by default implement an affine operation on the input features. To obtain a strictly linear (filtering) operation, use the default 'BiasInitializer' which is 'zeros' and set the bias learn rate factor of the layer to 0. This means that the bias is initialized to 0 and never changes during training. The network uses a custom initialization of the filter weights to be a scaled Kronecker delta sequence. This is an allpass filter, which performs no filtering of the input. The code for the allpass filter weight initializer is shown here.

function delta = kronDelta(sz)
% This function is only for use in the "Learn Pre-Emphasis Filter using
% Deep Learning" example. It may change or be removed in a
% future release.

L = sz(1);
delta = zeros(L,sz(2),sz(3),'single');
delta(1) = 1/sqrt(L);

end

stftLayer takes the filtered batch of input signals and obtains their magnitude STFTs. The magnitude STFT is a 2-D representation of the signal, which is amenable to use in 2-D convolutional networks.

While the weights of the STFT are not changed here during training, the layer supports backpropagation, which enables the filter coefficients in the "pre-emphasis-filter" layer to be learned.

Network Training

Set the training options for the custom training loop. Use 70 epochs with a minibatch size of 128. Set the initial learn rate to 0.001.

NumEpochs = 70;
miniBatchSize = 128;
learnRate = 0.001;

In the custom training loop, use a minibatchqueue object. The processSpeechMB function reads in a minibatch and applies a one-hot encoding scheme to the labels.

mbqTrain = minibatchqueue(transTrain,2,...
    'MiniBatchSize',miniBatchSize,...
    'MiniBatchFormat', {'CBT','CB'}, ... 
    'MiniBatchFcn', @processSpeechMB);

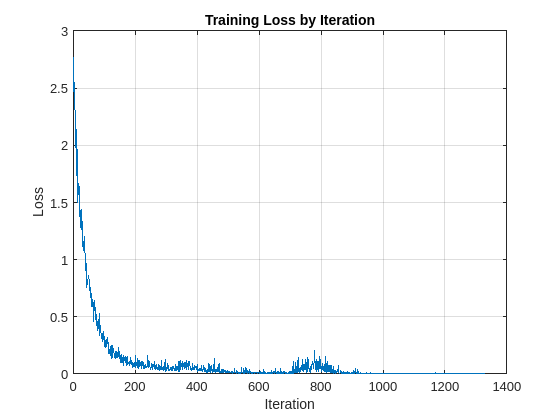
Train the network and plot the loss for each iteration. Use an Adam optimizer to update the network learnable parameters. To plot the loss as training progress, set the value of progress in the following code to "training-progress".

progress = "final-loss";
if progress == "training-progress"
    figure
    lineLossTrain = animatedline;
    ylim([0 inf])
    xlabel("Iteration")
    ylabel("Loss")
    grid on
end

% Initialize some training loop variables
trailingAvg = [];
trailingAvgSq = [];
iteration = 0;
lossByIteration = 0;

% Loop over epochs and time the epochs
start = tic;

for epoch = 1:NumEpochs
    reset(mbqTrain)
    shuffle(mbqTrain)

    % Loop over mini-batches
    while hasdata(mbqTrain)
        iteration = iteration + 1;
        
        % Get the next minibatch and one-hot coded targets
        [dlX,Y] = next(mbqTrain);
        
        % Evaluate the model gradients and loss 
        [gradients, loss, state] = dlfeval(@modelGradSTFT,dlnet,dlX,Y);
        if progress == "final-loss"
            lossByIteration(iteration) = loss;
        end

        % Update the network state
        dlnet.State = state;
        
        % Update the network parameters using an Adam optimizer
        [dlnet,trailingAvg,trailingAvgSq] = adamupdate(...
            dlnet,gradients,trailingAvg,trailingAvgSq,iteration,learnRate);        
        
        % Display the training progress
        D = duration(0,0,toc(start),'Format','hh:mm:ss');
        if progress == "training-progress"
            addpoints(lineLossTrain,iteration,loss)
            title("Epoch: " + epoch + ", Elapsed: " + string(D))
        end
        
    end
    disp("Training loss after epoch " + epoch + ": " + loss); 

end

Training loss after epoch 1: 1.5686
Training loss after epoch 2: 1.2063
Training loss after epoch 3: 0.70384
Training loss after epoch 4: 0.50291
Training loss after epoch 5: 0.35332
Training loss after epoch 6: 0.22536
Training loss after epoch 7: 0.14302
Training loss after epoch 8: 0.14749
Training loss after epoch 9: 0.1436
Training loss after epoch 10: 0.092127
Training loss after epoch 11: 0.053437
Training loss after epoch 12: 0.059123
Training loss after epoch 13: 0.07433
Training loss after epoch 14: 0.066282
Training loss after epoch 15: 0.11964
Training loss after epoch 16: 0.087663
Training loss after epoch 17: 0.069451
Training loss after epoch 18: 0.11175
Training loss after epoch 19: 0.044604
Training loss after epoch 20: 0.064503
Training loss after epoch 21: 0.050275
Training loss after epoch 22: 0.022125
Training loss after epoch 23: 0.092534
Training loss after epoch 24: 0.1393
Training loss after epoch 25: 0.015846
Training loss after epoch 26: 0.022516
Training loss after epoch 27: 0.01798
Training loss after epoch 28: 0.012391
Training loss after epoch 29: 0.0068496
Training loss after epoch 30: 0.036968
Training loss after epoch 31: 0.014514
Training loss after epoch 32: 0.0055389
Training loss after epoch 33: 0.0080868
Training loss after epoch 34: 0.0097247
Training loss after epoch 35: 0.0067841
Training loss after epoch 36: 0.0073048
Training loss after epoch 37: 0.0068763
Training loss after epoch 38: 0.064052
Training loss after epoch 39: 0.029343
Training loss after epoch 40: 0.055245
Training loss after epoch 41: 0.20821
Training loss after epoch 42: 0.052951
Training loss after epoch 43: 0.034677
Training loss after epoch 44: 0.020905
Training loss after epoch 45: 0.077562
Training loss after epoch 46: 0.0055673
Training loss after epoch 47: 0.015712
Training loss after epoch 48: 0.011886
Training loss after epoch 49: 0.0063345
Training loss after epoch 50: 0.0030241
Training loss after epoch 51: 0.0033596
Training loss after epoch 52: 0.0042235
Training loss after epoch 53: 0.0054001
Training loss after epoch 54: 0.0037229
Training loss after epoch 55: 0.0042717
Training loss after epoch 56: 0.0030938
Training loss after epoch 57: 0.0024514
Training loss after epoch 58: 0.005746
Training loss after epoch 59: 0.0027509
Training loss after epoch 60: 0.0069394
Training loss after epoch 61: 0.0024441
Training loss after epoch 62: 0.0054856
Training loss after epoch 63: 0.0012796
Training loss after epoch 64: 0.0013482
Training loss after epoch 65: 0.0038288
Training loss after epoch 66: 0.0013217
Training loss after epoch 67: 0.0022817
Training loss after epoch 68: 0.0025086
Training loss after epoch 69: 0.0013634
Training loss after epoch 70: 0.0014228

if progress == "final-loss"
        plot(1:iteration,lossByIteration)
        grid on 
        title('Training Loss by Iteration')
        xlabel("Iteration")
        ylabel("Loss")
end

Test the trained network on the held-out test set. Use a minibatchqueue object with a minibatch size of 32.

miniBatchSize = 32;
mbqTest = minibatchqueue(transTest,2,...
    'MiniBatchSize',miniBatchSize,...
    'MiniBatchFormat', {'CBT','CB'}, ... 
    'MiniBatchFcn', @processSpeechMB);

Loop over the test set and predict the class labels for each minibatch.

numObservations = numel(adsTest.Files);
classes = string(unique(adsTest.Labels));

predictions = [];

% Loop over mini-batches
while hasdata(mbqTest)    
    % Read mini-batch of data
    dlX = next(mbqTest);

    % Make predictions on the minibatch
    dlYPred = predict(dlnet,dlX);

    % Determine corresponding classes
    predBatch = onehotdecode(dlYPred,classes,1);
    predictions = [predictions predBatch];  
end

Evaluate the classification accuracy on the 600 examples in the held-out test set.

accuracy = mean(predictions' == categorical(adsTest.Labels))

accuracy = 0.9883

Test performance is approximately 99%. You can comment out the 1-D convolution layer and retrain the network without the pre-emphasis filter. The test performance without the pre-emphasis filter is also excellent at approximately 96%, but the use of the pre-emphasis filter makes a small improvement. It is noteworthy, that while the use of the learned pre-emphasis filter has only improved the test accuracy slightly, this was achieved by adding only 5 learnable parameters to the network.

To examine the learned pre-emphasis filter, extract the weights of the 1-D convolutional layer. Plot the frequency response. Recall that the sampling frequency of the data is 8 kHz. Because we initialized the filter to a scaled Kronecker delta sequence (allpass filter), we can easily compare the frequency response of the initialized filter with the learned response.

FIRFilter = dlnet.Layers(2).Weights;
[H,W] = freqz(FIRFilter,1,[],8000);
delta = kronDelta([5 1 1]);
Hinit = freqz(delta,1,[],4000);
plot(W,20*log10(abs([H Hinit])),'linewidth',2)
grid on
xlabel('Hz')
ylabel('dB')
legend('Learned Filter','Initial Filter','Location','SouthEast')
title('Learned Pre-emphasis Filter')

This example showed how to learn a pre-emphasis filter as a preprocessing step in a 2-D convolutional network based on short-time Fourier transforms of the signals. The ability of stftLayer to support backpropagation enabled gradient-based optimization of the filter weights inside the deep network. While this resulted in only a small improvement in the performance of the network on the test set, it achieved this improvement with a trivial increase in the number of learnable parameters.

Appendix: Helper Functions

function [out,info] = helperReadData(x,info)
% This function is only for use in the "Learn Pre-Emphasis Filter using
% Deep Learning" example. It may change or be removed in a
% future release.

N = numel(x);
x = single(x);
if N > 8192
    x = x(1:8192);
elseif N < 8192
    pad = 8192-N;
    prepad = floor(pad/2);
    postpad = ceil(pad/2);
    x = [zeros(prepad,1) ; x ; zeros(postpad,1)];
end
x = (x-mean(x))./std(x);
x = x(:)';
out = {x,info.Label};
end

function [dlX,dlY] = processSpeechMB(Xcell,Ycell)
% This function is only for use in the "Learn Pre-Emphasis Filter using
% Deep Learning" example. It may change or be removed in a
% future release.

Xcell = cellfun(@(x)reshape(x,1,1,[]),Xcell,'uni',false);
dlX = cat(2,Xcell{:});
dlY = cat(2,Ycell{:});
dlY = onehotencode(dlY,1);
end

function [grads,loss,state] = modelGradSTFT(net,X,T)
% This function is only for use in the "Learn Pre-Emphasis Filter using
% Deep Learning" example. It may change or be removed in a
% future release.

[y,state] = net.forward(X);
loss = crossentropy(y,T);
grads = dlgradient(loss,net.Learnables);
loss = double(gather(extractdata(loss)));
end