The filter Function

filter is implemented as the transposed direct-form II structure, where n–1 is the filter order. This is a canonical form that has the minimum number of delay elements.

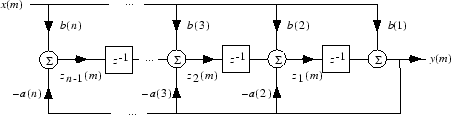
At sample m, filter computes the difference equations

$$\begin{array}{c}y(m)=b(1)x(m)+z_1(m-1)\\ z_1(m)=b(2)x(m)+z_2(m-1)-a(2)y(m)\\ ⋮=⋮\\ z_{n-2}(m)=b(n-1)x(m)+z_{n-1}(m-1)-a(n-1)y(m)\\ z_{n-1}(m)=b(n)x(m)-a(n)y(m)\end{array}$$

In its most basic form, filter initializes the delay outputs z_i(1), i = 1, ..., n-1 to 0. This is equivalent to assuming both past inputs and outputs are zero. Set the initial delay outputs using a fourth input parameter to filter, or access the final delay outputs using a second output parameter:

[y,zf] = filter(b,a,x,zi)

Access to initial and final conditions is useful for filtering data in sections, especially if memory limitations are a consideration. Suppose you have collected data in two segments of 5000 points each:

x1 = randn(5000,1);  % Generate two random data sequences.
x2 = randn(5000,1); 

Perhaps the first sequence, x1, corresponds to the first 10 minutes of data and the second, x2, to an additional 10 minutes. The whole sequence is x = [x1;x2]. If there is not sufficient memory to hold the combined sequence, filter the subsequences x1 and x2 one at a time. To ensure continuity of the filtered sequences, use the final conditions from x1 as initial conditions to filter x2:

[y1,zf] = filter(b,a,x1);
y2 = filter(b,a,x2,zf);

The filtic function generates initial conditions for filter. filtic computes the delay vector to make the behavior of the filter reflect past inputs and outputs that you specify. To obtain the same output delay values zf as above using filtic, use

zf = filtic(b,a,flipud(y1),flipud(x1));

This can be useful when filtering short data sequences, as appropriate initial conditions help reduce transient startup effects.