Model a Bouncing Ball in Continuous Time
This example shows how to configure a Stateflow® chart that simulates a bouncing ball in continuous time. The ball moves continuously through the air until it hits the ground, at which point a discontinuity occurs. As a result, the ball suddenly changes direction and velocity. For more information, see Continuous-Time Modeling in Stateflow.
The model sf_bounce contains a chart that updates in continuous time. Local variables describe the dynamics of a free-falling ball in terms of position and velocity. During simulation, the model uses zero-crossing detection to determine when the ball hits the ground.
Dynamics of a Bouncing Ball
You can specify how a ball falls freely under the force of gravity in terms of position p and velocity v with this system of first-order differential equations:
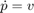

When p <= 0, the ball hits the ground and bounces. You can model the bounce by updating the position and velocity of the ball:
Reset the position to p = 0.
Reset the velocity to the negative of its value just before the ball hit the ground.
To account for energy loss, multiply the new velocity by a coefficient of distribution (-0.8).
Configure Chart for Continuous-Time Simulation
In the model, the BouncingBall chart implements modal logic to simulate the continuous dynamics of free fall and the discrete changes associated with bouncing. In the Chart properties dialog box, these settings enable the BouncingBall chart to simulate in continuous time:
Update method is
Continuousso the chart employs continuous-time simulation to model the dynamics of the bouncing ball.Enable zero-crossing detection is selected so the Simulink® solver can determine exactly when the ball hits the ground. Otherwise, the Simulink model cannot simulate the physics accurately and the ball appears to descend below ground.
Define Continuous-Time Variables
The BouncingBall chart has two continuous-time variables: p for position and v for velocity. For each of these variables:
Scope is
Local.Type is
double.Update Method is
Continuous.
To expose the continuous state of the chart to the Simulink model, the BouncingBall chart has two output variables: p_out and v_out. For each of these variables:
Scope is
Output.Type is
double.Update Method is
Discrete.
The chart defines the time derivative of continuous-time variables implicitly:
p_dotis the derivative of positionp.v_dotas the derivative of velocityv.
In the Model Explorer, you can view the continuous-time local variables and the corresponding outputs in the chart. Implicit derivative variables do not appear in the Model Explorer or in the Symbols pane.

Model Continuous Dynamics of Free Fall
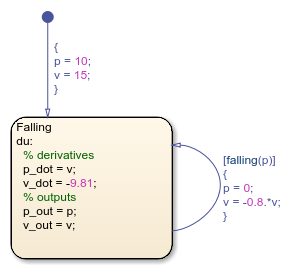
The BouncingBall chart consists of a single state named Falling that numerically solves the differential equations for free fall. The default transition into the state sets the initial position to 10 m and the initial velocity to 15 m/s. The during actions in the state:
Define the derivatives of position and velocity
Assign the values of the position and velocity of the ball to the output variables
p_outandv_out
Model Discrete Effects of the Bounce
The Falling state has a self-loop transition that models the discontinuity of the bounce as an instantaneous mode change when the ball suddenly reverses direction. The condition on the transition calls the edge detection operator falling. This operator determines when the ball hits the ground by detecting when the position crosses a threshold of zero and becomes negative. If the condition is valid, the condition action resets the position and velocity when the ball hits the ground.
Validate Chart Semantics
The BouncingBall chart meets the design requirements defined in Guidelines for Continuous-Time Simulation. In particular, the chart:
Initializes the local variables p and v on the default transition
Assigns values to the derivatives p_dot and v_dot in a
duringactionWrites to local variables p and v in a transition action
Does not contain events, inner transitions, event-based temporal logic, or change detection operators
View Simulation Results
After you run the model, the Scope block graphs the position and the velocity of the ball. The position graph exhibits the expected bounce pattern.
