Simplify Symbolic Expression

Simplify symbolic expressions in Live Editor

Description

The Simplify Symbolic Expression task enables you to interactively simplify or rearrange symbolic expressions. The task automatically generates MATLAB^® code for your live script. For more information about Live Editor tasks, see Add Interactive Tasks to a Live Script.

Using this task, you can:

• Perform algebraic simplification of symbolic expressions.

• Rewrite expressions in terms of another function.

• Expand algebraic expressions.

• Combine terms of identical algebraic structure.

• Generate the code used to simplify or rearrange expressions.

More

Related Functions

The code that Simplify Symbolic Expression generates to simplify expressions uses these functions.

• simplify

• simplifyFraction

• rewrite

• expand

• combine

×

Open the Task

To add the Simplify Symbolic Expression task to a live script in the MATLAB Editor:

• On the Live Editor tab, select Task > Simplify Symbolic Expression.

• In a code block in your script, type a relevant keyword, such as simplify, symbolic, rewrite, expand, or combine. Select Simplify Symbolic Expression from the suggested command completions.

Examples

Related Examples

• Add Interactive Tasks to a Live Script
• Simplify Symbolic Expressions Using Live Editor Task

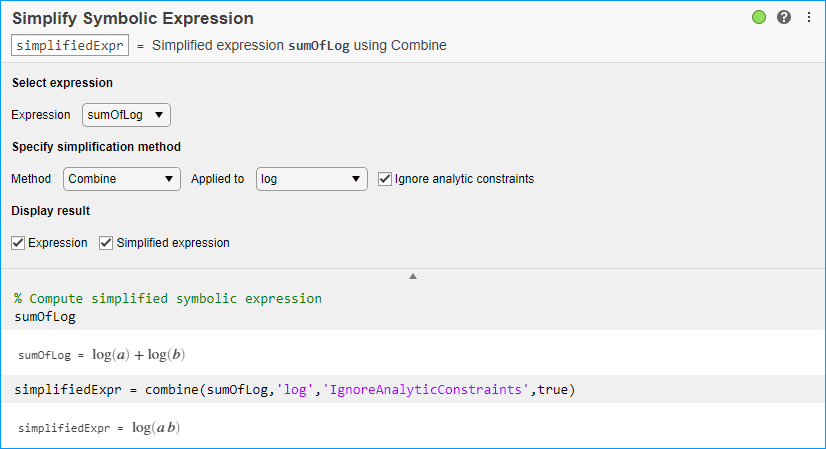
Parameters

Method — Specify simplification method

Simplify (default) | Simplify fraction | Rewrite | Expand | Combine

Specify the simplification method from the drop-down list:

Simplification Method	Description
Simplify	Perform algebraic simplification.
Simplify fraction	Simplify symbolic rational expressions.
Rewrite	Rewrite expressions in terms of another function.
Expand	Expand expressions and simplify inputs of functions by using identities.
Combine	Combine terms of identical algebraic structure.

Effort — Specify computational effort used to simplify

Minimum (default) | Low | Medium | High | Full

Specify the computational effort used for the Simplify method from the drop-down list:

Simplification Effort	Description
Minimum	Minimum effort with fastest computation time (can return most complicated result)
Low	Low effort with faster computation time
Medium	Medium effort with normal computation time
High	High effort with slower computation time
Full	Full effort with slowest computation time (can return simplest result)

Multiply out brackets — Multiply out brackets when expanding expressions

off (default) | on

Select this check box to not expand special functions for the Expand method. This option expands the arithmetic part of an expression, such as powers and roots, without expanding trigonometric, hyperbolic, logarithmic, and special functions.

Ignore analytic constraints — Ignore analytic constraints when expanding expressions

off (default) | on

Select this check box to apply purely algebraic simplifications to the Expand method, such as log(a) + log(b) = log(a*b) with the assumption that a and b are real positive numbers. Setting Ignore analytic constraints to on can give you simpler solutions, which could lead to results not generally valid. This option applies mathematical identities that are convenient for most engineering workflow, but do not always hold for all values of variables. In some cases, this option can lead to simpler results that are not equivalent to the initial expression. For details, see Algorithms.

Algorithms

When you use Ignore analytic constraints, then the simplification follows these rules:

• log(a) + log(b) = log(a·b) for all values of a and b. In particular, the following equality is valid for all values of a, b, and c :

    (a·b)^c = a^c·b^c.

• log(a^b) = b·log(a) for all values of a and b. In particular, the following equality is valid for all values of a, b, and c :

    (a^b)^c = a^b·c.

• If f and g are standard mathematical functions and f(g(x)) = x for all small positive numbers, f(g(x)) = x is assumed to be valid for all complex values of x. In particular:

  • log(e^x) = x

  • asin(sin(x)) = x, acos(cos(x)) = x, atan(tan(x)) = x

  • asinh(sinh(x)) = x, acosh(cosh(x)) = x, atanh(tanh(x)) = x

  • W_k(x·e^x) = x for all branch indices k of the Lambert W function.