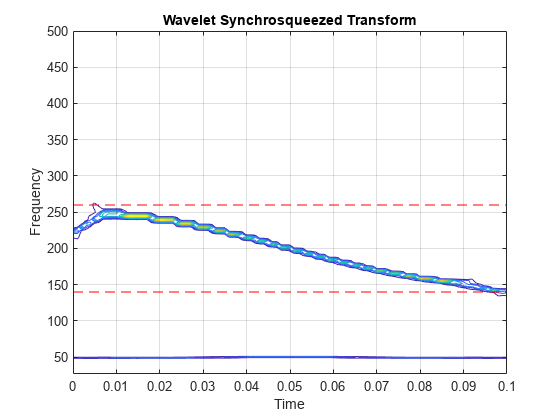
iwsst
Inverse wavelet synchrosqueezed transform
Syntax
Description
xrec = iwsst(sst)sst.
The iwsst function assumes that you obtained
sst using the wsst function with default
parameters.
Note
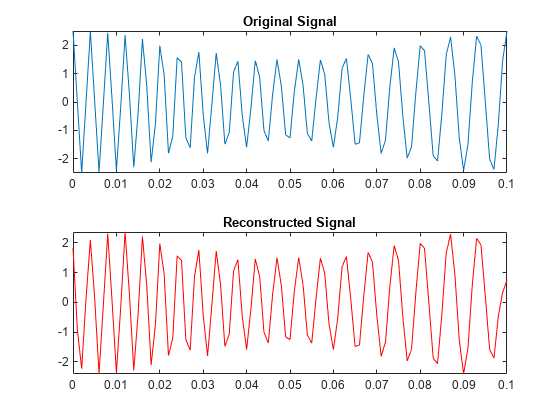
The wavelet synchrosqueezed transform does not preserve the signal mean. After inverting the synchrosqueezed transform, you must add the original signal mean.
The inverse wavelet synchrosqueezed transform is an approximate inverse which is not guaranteed to provide perfect reconstruction.
xrec = iwsst(___,Name=Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Daubechies, I., J. Lu, and H. T. Wu. "Synchrosqueezed Wavelet Transforms: an Empirical Mode Decomposition-like Tool." Applied and Computational Harmonic Analysis, Vol. 30, Number 2, 2011, pp. 243–261.
[2] Thakur, G., E. Brevdo, N. S. Fučkar, and H. T. Wu. "The Synchrosqueezing algorithm for time-varying spectral analysis: robustness properties and new paleoclimate applications." Signal Processing, Vol. 93, Number 5, 2013, pp. 1079–1094.