Results for

Iraj Hosseini, Ph.D., of Genentech will present a webinar on gPKPDSim , a MATLAB app that facilitates non-modelers to explore and simulate PKPD models built in SimBiology.

While model development typically requires mathematical modeling expertise, model exploration and simulation could be performed by non-modeler scientists to support experimental studies. Dr. Hosseini and his colleagues collaborate with MathWorks' consulting services to develop an App to enable easy use of any model constructed in SimBiology to execute common PKPD analyses.

Webinar will be hosted by Rosa & Co. on Wednesday October 24. To register, go to: https://register.gotowebinar.com/register/7922912955745684993?mw

This project presents a SimBiology implementation of Mager and Jusko’s generic Target-Mediated Drug Disposition model (TMDD) as described in "General pharmacokinetic model for drugs exhibiting target-mediated drug disposition". Target-mediated drug disposition is a common source of nonlinearity in PK profiles for biotherapeutics. Nonlinearities are introduced because drug-target bindings saturate at therapeutic dosing levels.

Drug in the Plasma reversibly binds with the unbound Target to form drug-target Complex. kon and koff are the association and dissociation rate constants, and clearance of free Drug and Complex from the Plasma is described by first-order processes with rate constants, kel and km, respectively. Free target turnover is described by a zero-order synthesis rate, ksyn, and a first order elimination (rate constant, kdeg). The model also includes an optional Tissue compartment to account for non-specific tissue binding or distribution.

References [1] Mager DE and Jusko WJ (2001) General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J Pharmacokinetics and Pharmacodynamics 28: 507–532.

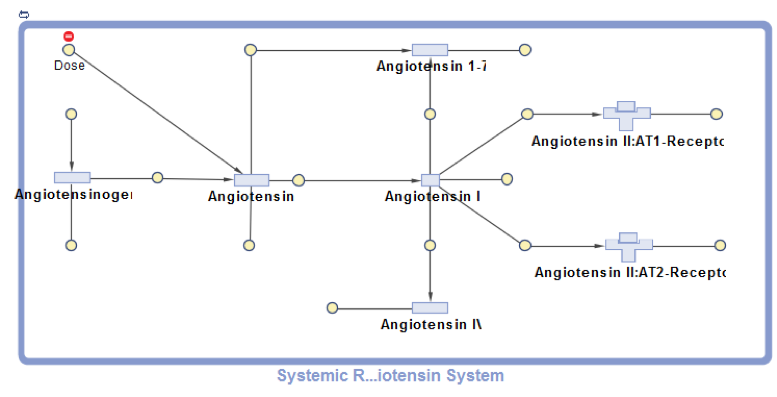
This project presents SimBiology model implementation of the systemic Renin-Angiotensin-System that was first developed by Lo et al. and used to investigate the effects of different RAS-modulating therapies. The RAS pathway is crucial for blood pressure and kidney function control as well as a range of other organism-wide functions. The model describes the enzymatic conversion of the precursor protein Angiotensinogen to Angiotensin I and its downstream products Angiotensin 1-7, Angiotensin II and Angiotensin IV. Key pathway effects are triggered by the association of Angiotensin II with the AT1-Receptor. A positive feedback loop connects the Angiotensin II–AT1-Receptor complex with the Angiotensinogen conversion (not shown in the diagram). Enzymatic reactions are modeled as pseudo-unimolecular using enzymatic activities as reaction rates. Degradation reactions are described using protein half-life times. Drug pharmacodynamics are included in the model using the term (1-DrugEffect), where DrugEffect follows a sigmoidal dependence on the Drug concentration, to modify the target enzyme activity.

References [1] Lo, A., Beh, J., Leon, H. D., Hallow, M. K., Ramakrishna, R., Rodrigo, M., & Sarkar, A. (2011). Using a Systems Biology Approach to Explore Hypotheses Underlying Clinical Diversity of the Renin Angiotensin System and the Response to Antihypertensive Therapies. Clinical Trial Simulations, 1, 457–482.

This project presents a SimBiology implementation of a physiologically-based pharmacokinetic (PBPK) model for trichloroethylene (TCE) and its metabolites. It is based on the article, “A human physiologically based pharmacokinetic model for trichloroethylene and its metabolites, trichloroacetic acid and free trichloroethanol” by Fisher et al. [1].

The human PBPK model for TCE and its metabolites presented here was developed by Fisher et al. [1] in order to assess human health risks associated with low level exposure to TCE. TCE is a commonly used solvent in the automotive and metal industries for vapor degreasing of metal parts. Exposure to TCE has been associated with toxic responses such as cancer formation and brain disorders in rodents and in humans [1]. In this PBPK model, TCE enters the systemic circulation through inhalation. Its disposition is described by a six-compartment model representing the liver, lung, kidney, fat, and slowly perfused and rapidly perfused tissues. In the liver, TCE is metabolized to trichloroacetic acid (TCA) and free trichloroethanol (TCOH-f) via P450-mediated metabolism where a fraction of TCOH-f is converted to TCA. For simplicity, a four-compartment submodel was used to describe the disposition of metabolites, TCA and TCOH-f, in the lung, liver, kidney, and body (muscle). Both metabolites are described to be excreted in the urine. TCOH-f is glucuronidated in the liver, forming glucuronide-bound TCOH (TCOH-b), and excreted in the urine via a saturable process whereas TCA is excreted by a first-order process by the kidney.

Reference: Fisher, J. W., Mahle, D., & Abbas, R. (1998). A human physiologically based pharmacokinetic model for trichloroethylene and its metabolites, trichloroacetic acid and free trichloroethanol. Toxicology and applied pharmacology, 152(2), 339-359.
I wrote a Cody problem, but I want to prevent people from using tricks to get a false "best" solution.
For example, many people do something like the following:
regexp '' '(?@"CODE HERE)';
in order to get the size of their program down to something quite small. I want to prevent this. I have seen people using some weird tests to try to block this, but I don't know how they work and when I try to copy them they fail.
Would it make sense that, in order to enhance coding experience with practice exercises, each section of the Matlab Academy courses reference specific CODY problems related to that section so the CODY problems can be used in parallel with the structure of the Matlab Academy courses?
I started with Cody today and I found the file calculateSize.m https://de.mathworks.com/matlabcentral/fileexchange/34754-calculate-size which should determine the size of my solution. Unfortunately I do not get it to run. Can someone explain this to me or maybe explain how exactly the size of the solution is calculated?
Gregory
Gregory
Last activity on 13 Jun 2017

Matlab webread (or urlread) Cody

Something seems to either have changed with webread/urlread behavior with R2016a or the Cody site has changed its authentication after it's September 2016 upgrade. Now, when ever I make a call using either webread (with weboptions) urlread using "My Cody" url, I get the html that corresponds to an unauthenticated user.
Ex: https://www.mathworks.com/matlabcentral/cody/players/1261697-gregory/solved
I've tried passing credentials using weboption and also cached the credentials using the built in Matlab browser - neither helped in seeing the authenticated version of this page.
Any help in understanding where the problem/solution lies would be helpful. Easily reproduced by running...
URL = 'https://www.mathworks.com/matlabcentral/cody/players/1261697-gregory/solved';
[Contents Status] = urlread(URL);
Compare this to the source pulled down when authenticated with Chrome (for example, search for the work "two"). FYI: this has worked for a couple of years up until now...
O45
O45
Last activity on 23 Oct 2018

Best solution to cody problems

Hi, I am uploading the answers to cody problems. Although most of answers are correct but my size is bigger than the best answer. How can I view the best answer?
James
James
Last activity on 11 Jun 2015

Issue with Cody Challenge Badges?

Apologies for putting this question here, but I'm not sure there's a specific forum for Cody-related questions.

I recently noticed that a new badge for "Magic Numbers Master" had been created and awarded. When I entered my profile to check that out, I noticed that I had received that badge, but lost the badge for "Cody Challenge Master." I thought that maybe my solution had been messed up because of a change in one of the test suites that my solution missed, as this has happened a number of times on other problems. According to the text underneath the badge icon, I've still solved all 96 of the questions in the Cody Challenge. All of the problems listed as part of that challenge are still marked as "Solved." Has anyone else run into this issue?

I created a solution for Cody Problem 1745 (Get me!) that is very simple and works perfectly on my computer; but in Cody, it results in the error:
Error: Undefined function or variable 'me'.
The test code is:
get = me();
y = rand(1,12345);
!rm now.m
!rm assert.m
assert(get == now)
My solution is:
classdef me
methods
function tf = eq(obj,~)
tf = true;
end
end
end
Why doesn't Cody accept this?
(P. S.) And why doesn't it accept function definitions like
function justDoIt
(which are appropriate for some problems and accepted by MATLAB) but requires at least one input and output?
Can anyone explain how Cody calculates the size of a program?
I read the help, but couldn't understand. :(
Why cody does not allow 'eval', 'evalc','feval' etc functions in the solutions? What is alternative to these functions?
e.g. I need to use:
if f='3*x'
x=0:10;
y=eval(vectorise(f))
so that values of y can be calculated as 3.*x
bt cody does not let us to use functions like eval
What is the alternative?
I have been stuck in the Cody question: Problem 31. Remove all the words that end with "ain"
http://www.mathworks.com/matlabcentral/cody/problems/31-remove-all-the-words-that-end-with-ain
for the whole afternoon. My codes below passed the first two tests but failed in the third one, because my codes cannot separate "" and ain. Anyone could help?
function s2 = remAin(s1)
s1_cell = strread(s1, '%s');
[s1_cell{find(not(cellfun('isempty', regexp(s1_cell, '\w*ain\>'))) == 1)}] = deal(' ');
s2 = strjoin(s1_cell');
s2 = strrep(s2, sprintf('%c%c%c', 32,32,32), sprintf('%c%c', 32,32));
if s2(end) == ' ' && s2(end-1) == ' '
s2(end) = [];
end
end
Salam,
While I was playing with Cody, I found one interesting question that asked to write MATLAB function to create times-table (can be found here: http://bit.ly/1cWZGGM ). The question itself was easy, but I had problems to figure out how could someone solve this problem with compact code of size 10 !!
After I've checked the leading answer, it seems to be written in Chinese not in MATLAB :)
Here is the answer:
function m = timestables(n)
regexp '' '(?@A=repmat([1:n]'',1,n);m=A.*A'';)'
end
Could anyone translate this to me so that I can use it in my future attempts ? :P
Regards.
In a previous Q & A, Jan Simon pointed to Cody: Sum 1:2^n. The current leading solution to that problem has node-count (or more simply, "length") 10. Apparently, 10 is the minimal length (per the official length-function on File Exchange) of any function taking input & generating output:
function y = test_cody_solution(x)
y = x;
end
Per Cody instruction examples, additional computation within a function definition increases the solution length. For example, both of the following functions have length 12:
function y = test_cody_solution(x)
y = [x];
end
function y = test_cody_solution(x)
y = x+1;
end
My question is: what kinds of ninja-style coding idioms even exist in MATLAB which actually perform definite computation but at the same time do not increase the node-count above 10? I'm not able to imagine what could be going on in order for someone to solve a given non-trivial Cody puzzle in length 10 or 11? IOW, without respect to any particular Cody problem, could someone please give an example of a non-trivial function which somehow comes in at or just above the absolute lower bound? Any explanation of the magic would be appreciated as well.
Thanks, Brad
function b = most_change(a)
a(:,1)=a(:,1)*0.25;
a(:,2)=a(:,2)*0.1;
a(:,3)=a(:,3)*0.05;
a(:,4)=a(:,4)*0.01;
d=sum(a,2);
c=max(d);
for i=1:length(d)
if d(i)==c
b=i;
end
end
i got wa please explain idont understand
Given a tic tac toe board:
1 represents X
0 represents empty.
-1 represents O
It is X's move. If there is an immediate win possibility, choose a square for an immediate win. Otherwise return 0.
Return absolute index of the square of choice. If multiple square are valid, return them in order.
Example:
Input a = [ 1 0 1
-1 1 0
0 -1 -1]
Output wins is [4 8]
Can anyone explain it in detail?
I'm confused with the sentence I marked ans bold style.
Thanks a lot~~~
I've written a valid answer to the last Cody problem, but it is not even close to the best answer. I have no idea how they made this short answer. To unlock it I need to solve another Cody question, but there are none left... :(
Anybody know how to unlock the last question?