36846
Results for
Yes, some readers might now argue that I used roughness in a crazy way in my last post, in my approach to finding a large twin prime pair. That is, I deliberately constructed a family of integers that were known to be a-priori rough. But, suppose I gave you some large, rather arbitrarily constructed number, and asked you to tell me if it is prime? For example, to pull a number out of my hat, consider
P = sym(2)^122397 + 65;
floor(vpa(log10(P) + 1))
36846 decimal digits is pretty large. And in fact, large enough that sym/isprime in R2024b will literally choke on it. But is it prime? Can we efficiently learn if it is at least not prime?
A nice way to learn the roughness of even a very large number like this is to use GCD.
gcd(P,prod(sym(primes(10000))))
If the greatest common divisor between P and prod(sym(primes(10000))) is 1, then P is NOT divisible by any small prime from that set, since they have no common divisors. And so we can learn that P is indeed fairly rough, 10000-rough in fact. That means P is more likely to be prime than most other large integers in that domain.
gcd(P,prod(sym(primes(100000))))
However, this rather efficiently tells us that in fact, P is not prime, as it has a common factor with some integer greater than 1, and less then 1e5.
I suppose you might think this is nothing different from doing trial divides, or using the mod function. But GCD is a much faster way to solve the problem. As a test, I timed the two.
timeit(@() gcd(P,prod(sym(primes(100000)))))
timeit(@() any(mod(P,primes(100000)) == 0))
Even worse, in the first test, much if not most of that time is spent in merely computing the product of those primes.
pprod = prod(sym(primes(100000)));
timeit(@() gcd(P,pprod))
So even though pprod is itself a huge number, with over 43000 decimal digits, we can use it quite efficiently, especially if you precompute that product if you will do this often.
How might I use roughness, if my goal was to find the next larger prime beyond 2^122397? I'll look fairly deeply, looking only for 1e7-rough numbers, because these numbers are pretty seriously large. Any direct test for primality will take some serious time to perform.
pprod = prod(sym(primes(10000000)));
find(1 == gcd(sym(2)^122397 + (1:2:199),pprod))*2 - 1
2^122397 plus any one of those numbers is known to be 1e7-rough, and therefore very possibly prime. A direct test at this point would surely take hours and I don't want to wait that long. So I'll back off just a little to identify the next prime that follows 2^10000. Even that will take some CPU time.
What is the next prime that follows 2^10000? In this case, the number has a little over 3000 decimal digits. But, even with pprod set at the product of primes less than 1e7, only a few seconds were needed to identify many numbers that are 1e7-rough.
P10000 = sym(2)^10000;
k = find(1 == gcd(P10000 + (1:2:1999),pprod))*2 - 1
k =
Columns 1 through 8
15 51 63 85 165 171 177 183
Columns 9 through 16
253 267 273 295 315 421 427 451
Columns 17 through 24
511 531 567 601 603 675 687 717
Columns 25 through 32
723 735 763 771 783 793 795 823
Columns 33 through 40
837 853 865 885 925 955 997 1005
Columns 41 through 48
1017 1023 1045 1051 1071 1075 1095 1107
Columns 49 through 56
1261 1285 1287 1305 1371 1387 1417 1497
Columns 57 through 64
1507 1581 1591 1593 1681 1683 1705 1771
Columns 65 through 69
1773 1831 1837 1911 1917
Among the 1000 odd numbers immediately following 2^10000, there are exactly 69 that are 1e7-rough. Every other odd number in that sequence is now known to be composite, and even though we don't know the full factorization of those 931 composite numbers, we don't care in the context as they are not prime. I would next apply a stronger test for primality to only those few candidates which are known to be rough. Eventually after an extensive search, we would learn the next prime succeeding 2^10000 is 2^10000+13425.
In my next post, I show how to use MOD, and all the cores in your CPU to test for roughness.
How can we use roughness in an effective context to identify large primes? I can quickly think of quite a few examples where we might do so. Again, remember I will be looking for primes with not just hundreds of decimal digits, or even only a few thousand digits. The eventual target is higher than that. Forget about targets for now though, as this is a journey, and what matters in this journey is what we may learn along the way.
I think the most obvious way to employ roughness is in a search for twin primes. Though not yet proven, the twin prime conjecture:
If it is true, it tells us there are infinitely many twin prime pairs. A twin prime pair is two integers with a separation of 2, such that both of them are prime. We can find quite a few of them at first, as we have {3,5}, {5,7}, {11,13}, etc. But there is only ONE pair of integers with a spacing of 1, such that both of them are prime. That is the pair {2,3}. And since primes are less and less common as we go further out, possibly there are only a finite number of twins with a spacing of exactly 2? Anyway, while I'm fairly sure the twin prime conjecture will one day be shown to be true, it can still be interesting to search for larger and larger twin prime pairs. The largest such known pair at the moment is
2996863034895*2^1290000 +/- 1
This is a pair with 388342 decimal digits. And while seriously large, it is still in range of large integers we can work with in MATLAB, though certainly not in double precision. In my own personal work on my own computer, I've done prime testing on integers (in MATLAB) with considerably more than 100,000 decimal digits.
But, again you may ask, just how does roughness help us here? In fact, this application of roughness is not new with me. You might want to read about tools like NewPGen {https://t5k.org/programs/NewPGen/} which sieves out numbers known to be composite, before any direct tests for primality are performed.
Before we even try to talk about numbers with thousands or hundreds of thousands of decimal digits, look at 6=2*3. You might observe
isprime([-1,1] + 6)
shows that both 5 and 7 are prime. This should not be a surprise, but think about what happens, about why it generated a twin prime pair. 6 is divisible by both 2 and 3, so neither 5 or 7 can possibly be divisible by either small prime as they are one more or one less than a multiple of both 2 and 3. We can try this again, pushing the limits just a bit.
isprime([-1,1] + 2*3*5)
That is again interesting. 30=2*3*5 is evenly divisible by 2, 3, and 5. The result is both 29 and 31 are prime, because adding 1 or subtracting 1 from a multiple of 2, 3, or 5 will always result in a number that is not divisible by any of those small primes. The next larger prime after 5 is 7, but it cannot be a factor of 29 or 31, since it is greater than both sqrt(29) and sqrt(31).
We have quite efficiently found another twin prime pair. Can we take this a step further? 210=2*3*5*7 is the smallest such highly composite number that is divisible by all primes up to 7. Can we use the same trick once more?
isprime([-1,1] + 2*3*5*7)
And here the trick fails, because 209=11*19 is not in fact prime. However, can we use the large twin prime trick we saw before? Consider numbers of the form [-1,1]+a*210, where a is itself some small integer?
a = 2;
isprime([-1,1] + a*2*3*5*7)
I did not need to look far, only out to a=2, because both 419 and 421 are prime. You might argue we have formed a twin prime "factory", of sorts. Next, I'll go out as far as the product of all primes not exceeding 60. This is a number with 22 decimal digits, already too large to represent as a double, or even as uint64.
prod(sym(primes(60)))
a = find(all(isprime([-1;1] + prod(sym(primes(60)))*(1:100)),1))
That easily identifies 3 such twin prime pairs, each of which has roughly 23 decimal digits, each of which have the form a*1922760350154212639070+/-1. The twin prime factory is still working well. Going further out to integers with 37 decimal digits, we can easily find two more such pairs that employ the product of all primes not exceeding 100.
prod(sym(primes(100)))
a = find(all(isprime([-1;1] + prod(sym(primes(100)))*(1:100)),1))
This is in fact an efficient way of identifying large twin prime pairs, because it chooses a massively composite number as the product of many distinct small primes. Adding or subtracting 1 from such a number will result always in a rough number, not divisible by any of the primes employed. With a little more CPU time expended, now working with numbers with over 1000 decimal digits, I will claim this next pair forms a twin prime pair, and is the smallest such pair we can generate in this way from the product of the primes not exceeding 2500.
isprime(7826*prod(sym(primes(2500))) + [-1 1])
ans =
logical
1
Unfortunately, 1000 decimal digits is at or near the limit of what the sym/isprime tool can do for us. It does beg the question, asking if there are alternatives to the sym/isprime tool, as an isProbablePrime test, usually based on Miller-Rabin is often employed. But this is gist for yet another set of posts.
Anyway, I've done a search for primes of the form
a*prod(sym(primes(10000))) +/- 1
having gone out as far as a = 600000, with no success as of yet. (My estimate is I will find a pair by the time I get near 5e6 for a.) Anyway, if others can find a better way to search for large twin primes in MATLAB, or if you know of a larger twin prime pair of this extended form, feel free to chime in.
My next post shows how to use GCD in a very nice way to identify roughness, on a large scale.
What is a rough number? What can they be used for? Today I'll take you down a journey into the land of prime numbers (in MATLAB). But remember that a journey is not always about your destination, but about what you learn along the way. And so, while this will be all about primes, and specifically large primes, before we get there we need some background. That will start with rough numbers.
Rough numbers are what I would describe as wannabe primes. Almost primes, and even sometimes prime, but often not prime. They could've been prime, but may not quite make it to the top. (If you are thinking of Marlon Brando here, telling us he "could've been a contender", you are on the right track.)
Mathematically, we could call a number k-rough if it is evenly divisible by no prime smaller than k. (Some authors will use the term k-rough to denote a number where the smallest prime factor is GREATER than k. The difference here is a minor one, and inconsequential for my purposes.) And there are also smooth numbers, numerical antagonists to the rough ones, those numbers with only small prime factors. They are not relevant to the topic today, even though smooth numbers are terribly valuable tools in mathematics. Please forward my apologies to the smooth numbers.
Have you seen rough numbers in use before? Probably so, at least if you ever learned about the sieve of Eratosthenes for prime numbers, though probably the concept of roughness was never explicitly discussed at the time. The sieve is simple. Suppose you wanted a list of all primes less than 100? (Without using the primes function itself.)
% simple sieve of Eratosthenes
Nmax = 100;
N = true(1,Nmax); % A boolean vector which when done, will indicate primes
N(1) = false; % 1 is not a prime by definition
nextP = find(N,1,'first'); % the first prime is 2
while nextP <= sqrt(Nmax)
% flag multiples of nextP as not prime
N(nextP*nextP:nextP:end) = false;
% find the first element after nextP that remains true
nextP = nextP + find(N(nextP+1:end),1,'first');
end
primeList = find(N)
Indeed, that is the set of all 25 primes not exceeding 100. If you think about how the sieve worked, it first found 2 is prime. Then it discarded all integer multiples of 2. The first element after 2 that remains as true is 3. 3 is of course the second prime. At each pass through the loop, the true elements that remain correspond to numbers which are becoming more and more rough. By the time we have eliminated all multiples of 2, 3, 5, and finally 7, everything else that remains below 100 must be prime! The next prime on the list we would find is 11, but we have already removed all multiples of 11 that do not exceed 100, since 11^2=121. For example, 77 is 11*7, but we already removed it, because 77 is a multiple of 7.
Such a simple sieve to find primes is great for small primes. However is not remotely useful in terms of finding primes with many thousands or even millions of decimal digits. And that is where I want to go, eventually. So how might we use roughness in a useful way? You can think of roughness as a way to increase the relative density of primes. That is, all primes are rough numbers. In fact, they are maximally rough. But not all rough numbers are primes. We might think of roughness as a necessary, but not sufficient condition to be prime.
How many primes lie in the interval [1e6,2e6]?
numel(primes(2e6)) - numel(primes(1e6))
There are 70435 primes greater than 1e6, but less than 2e6. Given there are 1 million natural numbers in that set, roughly 7% of those numbers were prime. Next, how many 100-rough numbers lie in that same interval?
N = (1e6:2e6)';
roughInd = all(mod(N,primes(100)) > 0,2);
sum(roughInd)
That is, there are 120571 100-rough numbers in that interval, but all those 70435 primes form a subset of the 100-rough numbers. What does this tell us? Of the 1 million numbers in that interval, approximately 12% of them were 100-rough, but 58% of the rough set were prime.
The point being, if we can efficiently identify a number as being rough, then we can substantially increase the chance it is also prime. Roughness in this sense is a prime densifier. (Is that even a word? It is now.) If we can reduce the number of times we need to perform an explicit isprime test, that will gain greatly because a direct test for primality is often quite costly in CPU time, at least on really large numbers.
In my next post, I'll show some ways we can employ rough numbers to look for some large primes.
I've been trying this problem a lot of time and i don't understand why my solution doesnt't work.
In 4 tests i get the error Assertion failed but when i run the code myself i get the diag and antidiag correctly.
function [diag_elements, antidg_elements] = your_fcn_name(x)
[m, n] = size(x);
% Inicializar los vectores de la diagonal y la anti-diagonal
diag_elements = zeros(1, min(m, n));
antidg_elements = zeros(1, min(m, n));
% Extraer los elementos de la diagonal
for i = 1:min(m, n)
diag_elements(i) = x(i, i);
end
% Extraer los elementos de la anti-diagonal
for i = 1:min(m, n)
antidg_elements(i) = x(m-i+1, i);
end
end
I noticed recently that my data is no longer updating on thingspeak again. Is there a connectivity issues with thingspeak
my code is as below:
#include "DHT.h"
#define DHTPIN 15 // what pin we're connected to
#define DHTTYPE DHT11
DHT dht(DHTPIN, DHTTYPE);
#define THINGSPEAK_API_KEY "1P4RY69D3YMP9R5W"
#include <SoftwareSerial.h>
#include <OneWire.h>
#include <DallasTemperature.h>
//-----------------------------
#include <ArduinoJson.h>
StaticJsonDocument<200>JsonDocument;
SoftwareSerialmyserial(10, 11);
//-------------------------
float voltage;
unsignedintfrac;
//---------------------
#define ONE_WIRE_BUS 5
OneWireoneWire(ONE_WIRE_BUS);
DallasTemperaturesensors(&oneWire);
floatCelcius = 0;
float Fahrenheit = 0;
//==========================================================================================================
bytesensorInterrupt = 0; // 0 = digital pin 2
bytesensorPin = 2;
// The hall-effect flow sensor outputs approximately 4.5 pulses per second per
// litre/minute of flow.
floatcalibrationFactor = 5.5; //==========================================================we change cal factor 4.5 to 5.5 if not work chnage again(4.5)
//========== 5.5 calibration factor is working efficent then 4.5 , 7.5 ,and 6.5
volatile byte pulseCount;
floatflowRate;
unsignedintflowMilliLitres;
unsigned long totalMilliLitres, tempTotal = -1;
unsigned long oldTime;
//-------------------------------------------------------
intpH_Value;
float Voltage;
//----------------------------------------------------------------------------------------------
void setup() {
// put your setup code here, to run once:
Serial.begin(9600);
myserial.begin(9600);
//--------------------------------
pinMode(sensorPin, INPUT);
digitalWrite(sensorPin, HIGH);
pulseCount = 0;
flowRate = 0.0;
flowMilliLitres = 0;
totalMilliLitres = 0; // ============================================================
oldTime = 0;
attachInterrupt(sensorInterrupt, pulseCounter, FALLING);
sensors.begin();
//------------------------------------------------
/********************GSM Communication Starts********************/
if (myserial.available())
Serial.write(myserial.read());
myserial.println("AT");
delay(1000);
myserial.println("AT+SAPBR=3,1,\"Contype\",\"GPRS\"");
delay(1000);
ShowSerialData();
myserial.println("AT+SAPBR=3,1,\"APN\",\"www\"");//APN
delay(1000);
ShowSerialData();
myserial.println("AT+SAPBR=1,1");
delay(1000);
ShowSerialData();
myserial.println("AT+SAPBR=2,1");
delay(1000);
ShowSerialData();
//---------------------------------
}
void loop() {
// put your main code here, to run repeatedly:
inti;
for (i = 0; i< 20; i++)
{
flow_meter();
}
temperature();
turbidity();
delay(1000);
gsm();
}
voidflow_meter()
{
if ((millis() - oldTime) > 1000) // Only process counters once per second
{
// Disable the interrupt while calculating flow rate and sending the value to
// the host
detachInterrupt(sensorInterrupt);
// Because this loop may not complete in exactly 1 second intervals we calculate
// the number of milliseconds that have passed since the last execution and use
// that to scale the output. We also apply the calibrationFactor to scale the output
// based on the number of pulses per second per units of measure (litres/minute in
// this case) coming from the sensor.
flowRate = ((1000.0 / (millis() - oldTime)) * pulseCount) / calibrationFactor;
// Note the time this processing pass was executed. Note that because we've
// disabled interrupts the millis() function won't actually be incrementing right
// at this point, but it will still return the value it was set to just before
// interrupts went away.
oldTime = millis();
// Divide the flow rate in litres/minute by 60 to determine how many litres have
// passed through the sensor in this 1 second interval, then multiply by 1000 to
// convert to millilitres.
flowMilliLitres = (flowRate / 60) * 1000;
// Add the millilitres passed in this second to the cumulative total
totalMilliLitres += flowMilliLitres;
// Print the flow rate for this second in litres / minute
/* Serial.print("Flow rate: ");
Serial.print(int(flowRate)); // Print the integer part of the variable
Serial.print("."); // Print the decimal point */
// Determine the fractional part. The 10 multiplier gives us 1 decimal place.
frac = (flowRate - int(flowRate)) * 10;
Serial.print(frac, DEC) ; // Print the fractional part of the variable
Serial.println("L/min");
/* // Print the number of litres flowed in this second
Serial.print(" Current Liquid Flowing: "); // Output separator
Serial.print(flowMilliLitres);
Serial.print("mL/Sec");
// Print the cumulative total of litres flowed since starting
Serial.print(" Output Liquid Quantity: "); // Output separator
Serial.print(totalMilliLitres);
Serial.println("mL"); */
if ( tempTotal != totalMilliLitres ) {
tempTotal = totalMilliLitres;
// displayVolumeOfWater(totalMilliLitres );
}
// Reset the pulse counter so we can start incrementing again
pulseCount = 0;
// Enable the interrupt again now that we've finished sending output
attachInterrupt(sensorInterrupt, pulseCounter, FALLING);
}
//=========================================================================================================================
}
voidpulseCounter()
{
// Increment the pulse counter
pulseCount++;
}
//-------------------------------------------------------------------------
void temperature()
{
sensors.requestTemperatures();
Celcius = sensors.getTempCByIndex(0);
Fahrenheit = sensors.toFahrenheit(Celcius);
Serial.print(" C ");
Serial.print(Celcius);
// Serial.print(" F ");
// Serial.println(Fahrenheit);
delay(1000);
}
//------------------------------------------------------------
void turbidity()
{
intsensorValue = analogRead(A0);
voltage = sensorValue * (5.0 / 1024.0);
// Serial.println ("Sensor Output (V):");
Serial.println (voltage);
// Serial.println();
delay(1000);
}
//------------------------------------------------------------
voidgsm()
{
myserial.println("AT+HTTPINIT");
delay(1000);
ShowSerialData();
myserial.println("AT+HTTPPARA=\"CID\",1");
delay(1000);
ShowSerialData();
StaticJsonDocument<200>JsonDocument;
JsonObject& object = JsonDocument.createObject();
object.set("TE", Celcius);
object.set("TU", voltage);
object.set("WF", frac);
delay(1000);
object.printTo(Serial);
Serial.println(" ");
String sendtoserver;
object.prettyPrintTo(sendtoserver);
delay(1000);
//myserial.println("AT+HTTPPARA=\"URL\",\"https://api.thingspeak.com/update?api_key=\""); //Server address
myserial.println("AT+HTTPPARA=\"URL\",\"https://api.thingspeak.com/update?api_key=\""); //Server address
delay(1000);
ShowSerialData();
myserial.println("AT+HTTPPARA=\"CONTENT\",\"application/json\"");
delay(1000);
ShowSerialData();
myserial.println("AT+HTTPDATA=" + String(sendtoserver.length()) + ",100000");
Serial.println(sendtoserver);
delay(1000);
ShowSerialData();
myserial.println(sendtoserver);
delay(2000);
ShowSerialData;
myserial.println("AT+HTTPACTION=1");
delay(1000);
ShowSerialData();
myserial.println("AT+HTTPREAD");
delay(1000);
ShowSerialData();
myserial.println("AT+HTTPTERM");
delay(1000);
ShowSerialData;
}
voidShowSerialData()
{
while (myserial.available() != 0)
Serial.write(myserial.read());
delay(1000);
}
My following code works running Matlab 2024b for all test cases. However, 3 of 7 tests fail (#1, #4, & #5) the QWERTY Shift Encoder problem. Any ideas what I am missing?
Thanks in advance.
keyboardMap1 = {'qwertyuiop[;'; 'asdfghjkl;'; 'zxcvbnm,'};
keyboardMap2 = {'QWERTYUIOP{'; 'ASDFGHJKL:'; 'ZXCVBNM<'};
if length(s) == 0
se = s;
end
for i = 1:length(s)
if double(s(i)) >= 65 && s(i) <= 90
row = 1;
col = 1;
while ~strcmp(s(i), keyboardMap2{row}(col))
if col < length(keyboardMap2{row})
col = col + 1;
else
row = row + 1;
col = 1;
end
end
se(i) = keyboardMap2{row}(col + 1);
elseif double(s(i)) >= 97 && s(i) <= 122
row = 1;
col = 1;
while ~strcmp(s(i), keyboardMap1{row}(col))
if col < length(keyboardMap1{row})
col = col + 1;
else
row = row + 1;
col = 1;
end
end
se(i) = keyboardMap1{row}(col + 1);
else
se(i) = s(i);
end
% if ~(s(i) = 65 && s(i) <= 90) && ~(s(i) >= 97 && s(i) <= 122)
% se(i) = s(i);
% end
end
Need code to collect data of waterflow sensor using ESP 8266 and to stoe it in ThingSpeak cloud
Ciao a Tutti,qualche mese fa avevo costruito una stazione meteo con un esp32 e vari sensori.
Tutto funzionava, adesso però ho riprovato, e non funziona più. Ho provato a creare un canale nuovo con nuovo ID canale, nuovo ID Client, nuovo Utente (uguale al Client) e nuova Password. si connette (ho inserito un comando se connesso a MQTT scrivi.....) ma non publica i dati.
Non reisco a saltarne fuori, ècambiato qualche cosa?
grazie a tutti
Hello,
could it be that there is currently is a stability problem with the MQTT-Broker? I can establisth a connection successfully using the MQTTX client (web and win64 installation). I tried all possible ports an connection types. It disconnects all the time after a few seconds of establishing a connection successfully. So it was not possible to subscribe any item. I do not think the problem is in my side... By the way, protocol verision 3.1.1 ist supported, 5.0 not, am I right?
Maybe you could give me a hint,
Best regards,
Manfred
in the below code write is working fine, but read is failing ( 404 error) can you please help me reslove this.
/*
Go to thingspeak.com and create an account if you don't have one already.
After logging in, click on the "New Channel" button to create a new channel for your data. This is where your data will be stored and displayed.
Fill in the Name, Description, and other fields for your channel as desired, then click the "Save Channel" button.
Take note of the "Write API Key" located in the "API keys" tab, this is the key you will use to send data to your channel.
Replace the channelID from tab "Channel Settings" and privateKey with "Read API Keys" from "API Keys" tab.
Replace the host variable with the thingspeak server hostname "api.thingspeak.com"
Upload the sketch to your ESP32 board and make sure that the board is connected to the internet. The ESP32 should now send data to your Thingspeak channel at the intervals specified by the loop function.
Go to the channel view page on thingspeak and check the "Field1" for the new incoming data.
You can use the data visualization and analysis tools provided by Thingspeak to display and process your data in various ways.
Please note, that Thingspeak accepts only integer values.
You can later check the values at https://thingspeak.com/channels/2005329
Please note that this public channel can be accessed by anyone and it is possible that more people will write their values.
*/
#include <WiFi.h>
const char *ssid = "xxxx"; // Change this to your WiFi SSID
const char *password = "xxxxx"; // Change this to your WiFi password
const char *host = "api.thingspeak.com"; // This should not be changed
const int httpPort = 80; // This should not be changed
const String channelID = "2805914"; // Change this to your channel ID
const String writeApiKey = "xxxxxxxxxxxxxxxx"; // Change this to your Write API key
const String readApiKey = "xxxxxxxxxxxxxxxx"; // Change this to your Read API key
// The default example accepts one data filed named "field1"
// For your own server you can ofcourse create more of them.
int field1 = 20;
//int field1 = 20;
int numberOfResults = 1; // Number of results to be read
int fieldNumber = 1; // Field number which will be read out
void setup() {
Serial.begin(115200);
while (!Serial) {
delay(100);
}
// We start by connecting to a WiFi network
Serial.println();
Serial.println("******************************************************");
Serial.print("Connecting to ");
Serial.println(ssid);
WiFi.begin(ssid, password);
while (WiFi.status() != WL_CONNECTED) {
delay(500);
Serial.print(".");
}
Serial.println("");
Serial.println("WiFi connected");
Serial.println("IP address: ");
Serial.println(WiFi.localIP());
}
void readResponse(NetworkClient *client) {
unsigned long timeout = millis();
while (client->available() == 0) {
if (millis() - timeout > 5000) {
Serial.println(">>> Client Timeout !");
client->stop();
return;
}
}
// Read all the lines of the reply from server and print them to Serial
while (client->available()) {
String line = client->readStringUntil('\r');
Serial.print(line);
}
Serial.printf("\nClosing connection\n\n");
}
void loop() {
NetworkClient client;
String footer = String(" HTTP/1.1\r\n") + "Host: " + String(host) + "\r\n" + "Connection: close\r\n\r\n";
// WRITE --------------------------------------------------------------------------------------------
if (!client.connect(host, httpPort)) {
return;
}
client.print("GET /update?api_key=" + writeApiKey + "&field1=" + field1 + footer);
readResponse(&client);
delay(200);
// READ --------------------------------------------------------------------------------------------
String readRequest = "GET /channels/" + channelID + "/fields/" + fieldNumber + ".json?results=" + numberOfResults + " HTTP/1.1\r\n" + "Host: " + host + "\r\n"
+ "Connection: close\r\n\r\n";
if (!client.connect(host, httpPort)) {
return;
}
client.print(readRequest);
readResponse(&client);
// -------------------------------------------------------------------------------------------------
//++field1;
delay(10000);
}
Thingspeak
Thingspeak channel shows a "watch" - "un-watch" selection box. What does this do?
Thanks
Dear Sir,
I login my channel in a device using my user name and password (also client id & password) but when I also login using the same user name and password in another device, the first one connection was forced disconnected. I want to publish via thinkspeak mqtt by using the two devices. Please advise how I can do it. Can I use the same thinkspeak user name to login? Is it needed to have another thinkspeak user to login? In this case, please also advise. Many thanks.
Aaron
If you have a folder with an enormous number of files and want to use the uigetfile function to select specific files, you may have noticed a significant delay in displaying the file list.
Thanks to the assistance from MathWorks support, an interesting behavior was observed.
For example, if a folder such as Z:\Folder1\Folder2\data contains approximately 2 million files, and you attempt to use uigetfile to access files with a specific extension (e.g., *.ext), the following behavior occurs:
Method 1: This takes minutes to show me the list of all files
[FileName, PathName] = uigetfile('Z:\Folder1\Folder2\data\*.ext', 'File selection');
Method 2: This takes less than a second to display all files.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data');
Method 3: This method also takes minutes to display the file list. What is intertesting is that this method is the same as Method 2, except that a file seperator "\" is added at the end of the folder string.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data\');
I was informed that the Mathworks development team has been informed of this strange behaviour.
I am using 2023a, but think this should be the same for newer versions.
This post is more of a "tips and tricks" guide than a question.
If you have a folder with an enormous number of files and want to use the uigetfile function to select specific files, you may have noticed a significant delay in displaying the file list.
Thanks to the assistance from MathWorks support, an interesting behavior was observed.
For example, if a folder such as Z:\Folder1\Folder2\data contains approximately 2 million files, and you attempt to use uigetfile to access files with a specific extension (e.g., *.ext), the following behavior occurs:
Method 1: This takes minutes to show me the list of all files
[FileName, PathName] = uigetfile('Z:\Folder1\Folder2\data\*.ext', 'File selection');
Method 2: This takes less than a second to display all files.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data');
Method 3: This method also takes minutes to display the file list. What is intertesting is that this method is the same as Method 2, except that a file seperator "\" is added at the end of the folder string.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data\');
I was informed that the Mathworks development team has been informed of this strange behaviour.
I am using 2023a, but think this should be the same for newer versions.
Christmas is coming, here are two dynamic Christmas tree drawing codes:
Crystal XMas Tree
function XmasTree2024_1
fig = figure('Units','normalized', 'Position',[.1,.1,.5,.8],...
'Color',[0,9,33]/255, 'UserData',40 + [60,65,75,72,0,59,64,57,74,0,63,59,57,0,1,6,45,75,61,74,28,57,76,57,1,1]);
axes('Parent',fig, 'Position',[0,-1/6,1,1+1/3], 'UserData',97 + [18,11,0,13,3,0,17,4,17],...
'XLim',[-1.5,1.5], 'YLim',[-1.5,1.5], 'ZLim',[-.2,3.8], 'DataAspectRatio', [1,1,1], 'NextPlot','add',...
'Projection','perspective', 'Color',[0,9,33]/255, 'XColor','none', 'YColor','none', 'ZColor','none')
%% Draw Christmas tree
F = [1,3,4;1,4,5;1,5,6;1,6,3;...
2,3,4;2,4,5;2,5,6;2,6,3];
dP = @(V) patch('Faces',F, 'Vertices',V, 'FaceColor',[0 71 177]./255,...
'FaceAlpha',rand(1).*0.2+0.1, 'EdgeColor',[0 71 177]./255.*0.8,...
'EdgeAlpha',0.6, 'LineWidth',0.5, 'EdgeLighting','gouraud', 'SpecularStrength',0.3);
r = .1; h = .8;
V0 = [0,0,0; 0,0,1; 0,r,h; r,0,h; 0,-r,h; -r,0,h];
% Rotation matrix
Rx = @(V, theta) V*[1 0 0; 0 cos(theta) sin(theta); 0 -sin(theta) cos(theta)];
Rz = @(V, theta) V*[cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0; 0 0 1];
N = 180; Vn = zeros(N, 3); eval(char(fig.UserData))
for i = 1:N
tV = Rz(Rx(V0.*(1.2 - .8.*i./N + rand(1).*.1./i^(1/5)), pi/3.*(1 - .6.*i./N)), i.*pi/8.1 + .001.*i.^2) + [0,0,.016.*i];
dP(tV); Vn(i,:) = tV(2,:);
end
scatter3(Vn(:,1).*1.02,Vn(:,2).*1.02,Vn(:,3).*1.01, 30, 'w', 'Marker','*', 'MarkerEdgeAlpha',.5)
%% Draw Star of Bethlehem
w = .3; R = .62; r = .4; T = (1/8:1/8:(2 - 1/8)).'.*pi;
V8 = [ 0, 0, w; 0, 0,-w;
1, 0, 0; 0, 1, 0; -1, 0, 0; 0,-1,0;
R, R, 0; -R, R, 0; -R,-R, 0; R,-R,0;
cos(T).*r, sin(T).*r, T.*0];
F8 = [1,3,25; 1,3,11; 2,3,25; 2,3,11; 1,7,11; 1,7,13; 2,7,11; 2,7,13;
1,4,13; 1,4,15; 2,4,13; 2,4,15; 1,8,15; 1,8,17; 2,8,15; 2,8,17;
1,5,17; 1,5,19; 2,5,17; 2,5,19; 1,9,19; 1,9,21; 2,9,19; 2,9,21;
1,6,21; 1,6,23; 2,6,21; 2,6,23; 1,10,23; 1,10,25; 2,10,23; 2,10,25];
V8 = Rx(V8.*.3, pi/2) + [0,0,3.5];
patch('Faces',F8, 'Vertices',V8, 'FaceColor',[255,223,153]./255,...
'EdgeColor',[255,223,153]./255, 'FaceAlpha', .2)
%% Draw snow
sXYZ = rand(200,3).*[4,4,5] - [2,2,0];
sHdl1 = plot3(sXYZ(1:90,1),sXYZ(1:90,2),sXYZ(1:90,3), '*', 'Color',[.8,.8,.8]);
sHdl2 = plot3(sXYZ(91:200,1),sXYZ(91:200,2),sXYZ(91:200,3), '.', 'Color',[.6,.6,.6]);
annotation(fig,'textbox',[0,.05,1,.09], 'Color',[1 1 1], 'String','Merry Christmas Matlaber',...
'HorizontalAlignment','center', 'FontWeight','bold', 'FontSize',48,...
'FontName','Times New Roman', 'FontAngle','italic', 'FitBoxToText','off','EdgeColor','none');
% Rotate the Christmas tree and let the snow fall
for i=1:1e8
sXYZ(:,3) = sXYZ(:,3) - [.05.*ones(90,1); .06.*ones(110,1)];
sXYZ(sXYZ(:,3)<0, 3) = sXYZ(sXYZ(:,3) < 0, 3) + 5;
sHdl1.ZData = sXYZ(1:90,3); sHdl2.ZData = sXYZ(91:200,3);
view([i,30]); drawnow; pause(.05)
end
end
Curved XMas Tree
function XmasTree2024_2
fig = figure('Units','normalized', 'Position',[.1,.1,.5,.8],...
'Color',[0,9,33]/255, 'UserData',40 + [60,65,75,72,0,59,64,57,74,0,63,59,57,0,1,6,45,75,61,74,28,57,76,57,1,1]);
axes('Parent',fig, 'Position',[0,-1/6,1,1+1/3], 'UserData',97 + [18,11,0,13,3,0,17,4,17],...
'XLim',[-6,6], 'YLim',[-6,6], 'ZLim',[-16, 1], 'DataAspectRatio', [1,1,1], 'NextPlot','add',...
'Projection','perspective', 'Color',[0,9,33]/255, 'XColor','none', 'YColor','none', 'ZColor','none')
%% Draw Christmas tree
[X,T] = meshgrid(.4:.1:1, 0:pi/50:2*pi);
XM = 1 + sin(8.*T).*.05;
X = X.*XM; R = X.^(3).*(.5 + sin(8.*T).*.02);
dF = @(R, T, X) surf(R.*cos(T), R.*sin(T), -X, 'EdgeColor',[20,107,58]./255,...
'FaceColor', [20,107,58]./255, 'FaceAlpha',.2, 'LineWidth',1);
CList = [254,103,110; 255,191,115; 57,120,164]./255;
for i = 1:5
tR = R.*(2 + i); tT = T+i; tX = X.*(2 + i) + i;
SFHdl = dF(tR, tT, tX);
[~, ind] = sort(SFHdl.ZData(:)); ind = ind(1:8);
C = CList(randi([1,size(CList,1)], [8,1]), :);
scatter3(tR(ind).*cos(tT(ind)), tR(ind).*sin(tT(ind)), -tX(ind), 120, 'filled',...
'CData', C, 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.3)
scatter3(tR(ind).*cos(tT(ind)), tR(ind).*sin(tT(ind)), -tX(ind), 60, 'filled', 'CData', C)
end
%% Draw Star of Bethlehem
Rx = @(V, theta) V*[1 0 0; 0 cos(theta) sin(theta); 0 -sin(theta) cos(theta)];
% Rz = @(V, theta) V*[cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0; 0 0 1];
w = .3; R = .62; r = .4; T = (1/8:1/8:(2 - 1/8)).'.*pi;
V8 = [ 0, 0, w; 0, 0,-w;
1, 0, 0; 0, 1, 0; -1, 0, 0; 0,-1,0;
R, R, 0; -R, R, 0; -R,-R, 0; R,-R,0;
cos(T).*r, sin(T).*r, T.*0];
F8 = [1,3,25; 1,3,11; 2,3,25; 2,3,11; 1,7,11; 1,7,13; 2,7,11; 2,7,13;
1,4,13; 1,4,15; 2,4,13; 2,4,15; 1,8,15; 1,8,17; 2,8,15; 2,8,17;
1,5,17; 1,5,19; 2,5,17; 2,5,19; 1,9,19; 1,9,21; 2,9,19; 2,9,21;
1,6,21; 1,6,23; 2,6,21; 2,6,23; 1,10,23; 1,10,25; 2,10,23; 2,10,25];
V8 = Rx(V8.*.8, pi/2) + [0,0,-1.3];
patch('Faces',F8, 'Vertices',V8, 'FaceColor',[255,223,153]./255,...
'EdgeColor',[255,223,153]./255, 'FaceAlpha', .2)
annotation(fig,'textbox',[0,.05,1,.09], 'Color',[1 1 1], 'String','Merry Christmas Matlaber',...
'HorizontalAlignment','center', 'FontWeight','bold', 'FontSize',48,...
'FontName','Times New Roman', 'FontAngle','italic', 'FitBoxToText','off','EdgeColor','none');
%% Draw snow
sXYZ = rand(200,3).*[12,12,17] - [6,6,16];
sHdl1 = plot3(sXYZ(1:90,1),sXYZ(1:90,2),sXYZ(1:90,3), '*', 'Color',[.8,.8,.8]);
sHdl2 = plot3(sXYZ(91:200,1),sXYZ(91:200,2),sXYZ(91:200,3), '.', 'Color',[.6,.6,.6]);
for i=1:1e8
sXYZ(:,3) = sXYZ(:,3) - [.1.*ones(90,1); .12.*ones(110,1)];
sXYZ(sXYZ(:,3)<-16, 3) = sXYZ(sXYZ(:,3) < -16, 3) + 17.5;
sHdl1.ZData = sXYZ(1:90,3); sHdl2.ZData = sXYZ(91:200,3);
view([i,30]); drawnow; pause(.05)
end
end
I wish all MATLABers a Merry Christmas in advance!
I have a device that via GPRS publish correctly, after autentication to the server mqtt3.thingspeak.com , a lot of datas like:
.{"sensorDatas":[{"flag":"COUNT","value":1},...........,{"flag":"AI1","value":25.80}]}
I configure a correct Channel with a field called AI1, but I can't fill it with that value 25.80.
I am sure that the device communicate to the server the string {"flag":"AI1","value":25.80} but nothing.
Could you tell me what I have to do? Probably I have to write some software code, may someone help me?
Are there some examples for a beginner like me?
Thank you very much
Hello
I am trying to connect Thingspeak to ibfluxdb. Is that possible? how you do that??
I am using a micro:bit device with ESP8266 for a IOT project, but cannot connect thingspeak recently.
The conncection is unstable, I can hardly connect to thingspeak for days, somehow it works last night for 30 mins and then it fails.
The program does not change and I have included a 25 sec delayed between each data sending.
Please advice why and how to fix it. Thank you.
Hi! My name is Mike McLernon, and I’m a product marketing engineer with MathWorks. In my role, I look at the trends ongoing in the wireless industry, across lots of different standards (think 5G, WLAN, SatCom, Bluetooth, etc.), and I seek to shape and guide the software that MathWorks builds to respond to these trends. That’s all about communicating within the Mathworks organization, but every so often it’s worth communicating these trends to our audience in the world at large. Many of the people reading this are engineers (or engineers at heart), and we all want to know what’s happening in the geek world around us. I think that now is one of these times to communicate an important milestone. So, without further ado . . .
Bluetooth 6.0 is here! Announced in September by the Bluetooth Special Interest Group (SIG), it’s making more advances in its quest to create a “world without wires”. A few of the salient features in Bluetooth 6.0 are:
- Channel sounding (for accurate distance measurements)
- Decision-based advertising filtering (for more efficient channel scanning)
- Monitoring advertisers (for improved energy efficiency when devices come into and go out of range)
- Frame space updates (for both higher throughput and better coexistence management)
Bluetooth 6.0 includes other features as well, but the SIG has put special promotional emphasis on channel sounding (CS), which once upon a time was called High Accuracy Distance Measurement (HADM). The SIG has said that CS is a step towards true distance awareness, and 10 cm ranging accuracy. I think their emphasis is in exactly the right place, so let’s learn more about this technology and how it is used.
CS can be used for the following use cases:
- Keyless vehicle entry, performed by communication between a key fob or phone and the car’s anchor points
- Smart locks, to permit access only when an authorized device is within a designated proximity to the locks
- Geofencing, to limit access to designated areas
- Warehouse management, to monitor inventory and manage logistics
- Asset tracking for virtually any object of interest
In the past, Bluetooth devices would use a received signal strength indicator (RSSI) measurement to infer the distance between two of them. They would assume a free space path loss on the link, and use a straightforward equation to estimate distance:
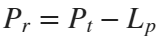
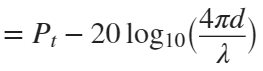
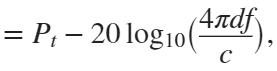where
received power in dBm,
transmitted power in dBm,
propagation loss in dB,
distance between the two devices, in m,
Bluetooth signal wavelength, in m,
Bluetooth signal frequency, in Hz,
speed of light (3 x 1e8 m/s).So in this method,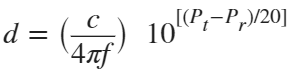 
. But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.
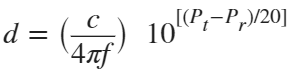. But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.Bluetooth 6.0 introduces not one, but two ways to accurately measure distance:
- Round-trip time (RTT) measurement
- Phase-based ranging (PBR) measurement
The RTT measurement method uses the fact that the Bluetooth signal time of flight (TOF) between two devices is half the RTT. It can then accurately compute the distance d as
, where c is again the speed of light. This method requires accurate measurements of the time of departure (TOD) of the outbound signal from device 1 (the Initiator), time of arrival (TOA) of the outbound signal to device 2 (the Reflector), TOD of the return signal from device 2, and TOA of the return signal to device 1. The diagram below shows the signal paths and the times.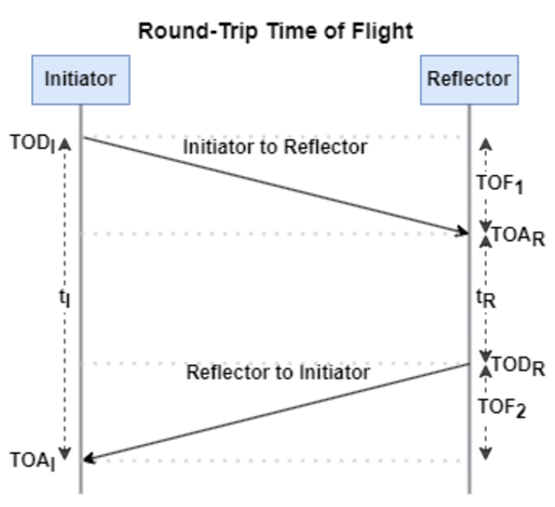
If you want to see how you can use MATLAB to simulate the RTT method, take a look at Estimate Distance Between Bluetooth LE Devices by Using Channel Sounding and Round-Trip Timing.
The PBR method uses two Bluetooth signals of different frequencies to measure distance. These signals are simply tones – sine waves. Without going through the derivation, PBR calculates distance d as
, where
distance between the two devices, in m,
speed of light (3 x 1e8 m/s),
phase measured at the Initiator after the tone at 
completes a round trip, in radians,
phase measured at the Initiator after the tone at 
completes a round trip, in radians,
frequency of the first tone, in Hz,
frequency of the second tone, in Hz.The mod() operation is needed to eliminate ambiguities in the distance calculation and the final division by two is to convert a round trip distance to a one-way distance. Because a given phase difference value can hold true for an infinite number of distance values, the mod() operation chooses the smallest distance that satisfies the equation. Also, these tones can be as close as 1 MHz apart. In that case, the maximum resolvable distance measurement is about 150 m. The plot below shows that ambiguity and repetition in distance measurement.
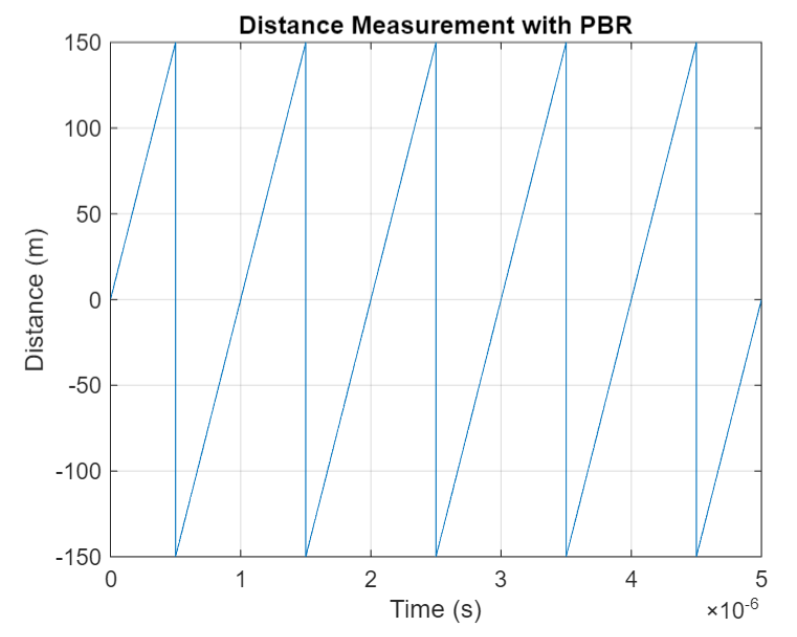
If you want to see how you can use MATLAB to simulate the PBR method, take a look at Estimate Distance Between Bluetooth LE Devices by Using Channel Sounding and Phase-Based Ranging.
Bluetooth 6.0 outlines RTT and PBR distance measurement methods, but CS does not mandate a specific algorithm for calculating distance estimates. This flexibility allows device manufacturers to tailor solutions to various use cases, balancing computational complexity with required accuracy and adapting to different radio environments. Examples include simple phase difference calculations and FFT-based methods.
Although Bluetooth 6.0 is now out, it is far from a finished version. The SIG is actively working through the ratification process for two major extensions:
- High Data Throughput, up to 8 Mbps
- 5 and 6 GHz operation
See the last few minutes of this video from the SIG to learn more about these exciting future developments. And if you want to see more Bluetooth blogs, give a review of this one! Finally, if you have specific Bluetooth questions, give me a shout and let’s start a discussion!
