Results for
Couldn’t catch everything at MATLAB EXPO 2025? You’re not alone. Across keynotes and track talks, there were too many gems for one sitting. For the next 9 weeks, we’ll reveal the "Top 10" sessions attended (workshops excluded)—one per week—so you can binge the best and compare notes with peers.
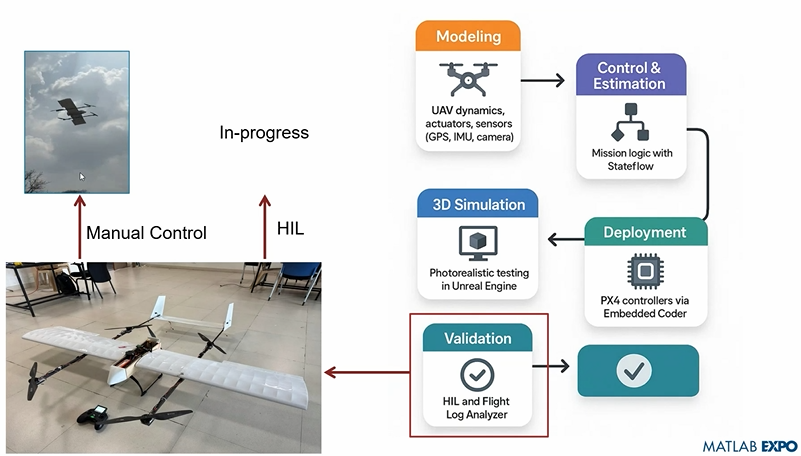
Starting at #10: Simulation-Driven Development of Autonomous UAVs Using MATLAB
A huge thanks to Dr. Shital S. Chiddarwar from Visvesvaraya National Institute of Technology Nagpur who delivered this presentation online at MATLAB EXPO 2025. Are you curious how this workflow accelerates development and boosts reliability?
I recently created a short 5-minute video covering 10 tips for students learning MATLAB. I hope this helps!
DocMaker allows you to create MATLAB toolbox documentation from Markdown documents and MATLAB scripts.
The MathWorks Consulting group have been using it for a while now, and so David Sampson, the director of Application Engineering, felt that it was time to share it with the MATLAB and Simulink community.
David listed its features as:
➡️ write documentation in Markdown not HTML
🏃 run MATLAB code and insert textual and graphical output
📜 no more hand writing XML index files
🕸️ generate documentation for any release from R2021a onwards
💻 view and edit documentation in MATLAB, VS Code, GitHub, GitLab, ...
🎉 automate toolbox documentation generation using MATLAB build tool
📃 fully documented using itself
😎 supports light, dark, and responsive modes
🐣 cute logo
I got an email message that says all the files I've uploaded to the File Exchange will be given unique names. Are these new names being applied to my files automatically? If so, do I need to download them to get versions with the new name so that if I update them they'll have the new name instead of the name I'm using now?
A coworker shared with me a hilarious Instagram post today. A brave bro posted a short video showing his MATLAB code… casually throwing 49,000 errors!
Surprisingly, the video went virial and recieved 250,000+ likes and 800+ comments. You really never know what the Instagram algorithm is thinking, but apparently “my code is absolutely cooked” is a universal developer experience 😂
Last note: Can someone please help this Bro fix his code?
In 2025, we saw the growing impact of GenAI on site traffic and user behavior across the entire technical landscape. Amid all this change, MATLAB Central continued to stand out as a trusted home for MATLAB and Simulink users. More than 11 million unique visitors in 2025 came to MATLAB Central to ask questions, share code, learn, and connect with one another.
Let’s celebrate what made 2025 memorable across three key areas: people, content, and events.
People
In 2025, nearly 20,000 contributors participated across the community. We’d like to spotlight a few standout contributors:
- @Sam Chak earned the Most Accepted Answers Badge for both 2024 and 2025. Sam is a rising star in MATLAB Answers with 2,000+ answers and 1,000+ votes.
- @Rodney Tan has been actively contributing files to File Exchange. In 2025, his submissions got almost 20,000 downloads!
- @Dyuman Joshi was recognized as a top contributor on both Cody and Answers. Many may not know that Dyuman is also a Cody moderator, doing tremendous behind-the-scenes moderation work to keep the platform running smoothly.
- A warm welcome to @Steve Eddins, who joined the Community Advisory Board. Steve brings a unique perspective as a former MathWorker and long-time top community contributor.
- Congratulations to @Walter Roberson on reaching 100 followers! MATLAB Central thrives on people-to-people connections, and we’d love to see even more of these relationships grow.
Of course, there are many contributors we didn’t mention here—thank you all for your outstanding contributions and for making the community what it is.
Content
Our high-quality community content not only attracts users but also helps power the broader GenAI ecosystem.
Popular Blog Post & File Exchange Submission
- Zoomed Axes, submitted by @Caleb Thomas, enables zoomed-in views of selected regions in a plot.This submission was featured in the Pick of the Week blog post, “MATLAB Zoomed Axes: Showing zoomed-in regions of a 2D plot,” which generated 5,000 views in just one month.
Popular Discussion Post
- What did MATLAB/Simulink users wait for most in 2025? It's R2025a! “Where is MATLAB R2025a?” became the most-viewed discussion post, with 10,000 views and 30 comments. Thanks for your patience — MATLAB R2025a turned out to be one of the biggest releases we’ve ever delivered.
Most Viewed Question
- “How do I create a for loop in MATLAB?” was the most-viewed community question of the year. It’s a fun reminder that even as MATLAB evolves, the basics remain essential — and always in demand.
Most Voted Poll
- “Did you know there is an official MATLAB certification?”, created by @goc3, was the most-voted poll of 2025.While 50% of respondents voted “No”, it’s exciting to see 3% are certified MATLAB Professionals. Will you be one of them in 2026?
Events
The Cody Contest 2025 brought teams together to tackle challenging but fun Cody problems. During the contest:
- 20,000+ solutions were submitted
- 20+ tips & tricks articles were shared by top players
While the contest has ended, you can still challenge yourself with the fun contest problem group. If you get stuck, the tips & tricks articles are a great resource—and you’ll be amazed by the creativity and skill of the contributors.
Thank you for being part of an incredible 2025. Your curiosity, generosity, and expertise are what make MATLAB Central a trusted home for millions—and we look forward to learning and growing together in 2026.
AI-assisted software development moves pretty fast! I recently noticed everyone in the AI community talking about a Simpson's character. I originally thought it was some joke-meme that I didn't understand but it turns out to be an AI development methodology claude-code/plugins/ralph-wiggum/README.md at main · anthropics/claude-code
I noticed that @Toshiaki Takeuchi mentioned it in my recent interview of him over at The MATLAB blog https://blogs.mathworks.com/matlab/2026/01/26/matlab-agentic-ai-the-workflow-that-actually-works/
Has anyone here tried this yet?
I gave it a try on my mac mini m4. I'm speechless 🤯
Currently, the open-source MATLAB Community is accessed via the desktop web interface, and the experience on mobile devices is not very good—especially switching between sections like Discussion, FEX, Answers, and Cody is awkward. Having a dedicated app would make using the community much more convenient on phones.
Similarty,github has Mobile APP, It's convient for me.
Educators in mid 2025 worried about students asking an AI to write their required research paper. Now, with agentic AI, students can open their LMS with say Comet and issue the prompt “Hey, complete all my assignments in all of my courses. Thanks!” Done. Thwarting illegitimate use of AIs in education without hindering the many legitimate uses is a cat-and-mouse game and burgeoning industry.
I am actually more interested in a new AI-related teaching and learning challenge: how one AI can teach another AI. To be specific, I have been discovering with Claude macOS App running Opus 4.5 how to school LM Studio macOS App running a local open model Qwen2.5 32B in the use of MATLAB and other MCP services available to both apps, so, like Claude, LM Studio can operate all of my MacOS apps, including regular (Safari) and agentic (Comet or Chrome with Claude Chrome Extension) browsers and other AI Apps like ChatGPT or Perplexity, and can write and debug MATLAB code agentically. (Model Context Protocol is the standardized way AI apps communicate with tools.) You might be playing around with multiple AIs and encountering similar issues. I expect the AI-to-AI teaching and learning challenge to go far beyond my little laptop milieu.
To make this concrete, I offer the image below, which shows LM Studio creating its first Excel spreadsheet using Excel macOS app. Claude App in the left is behind the scenes there updating LM Studio's context window.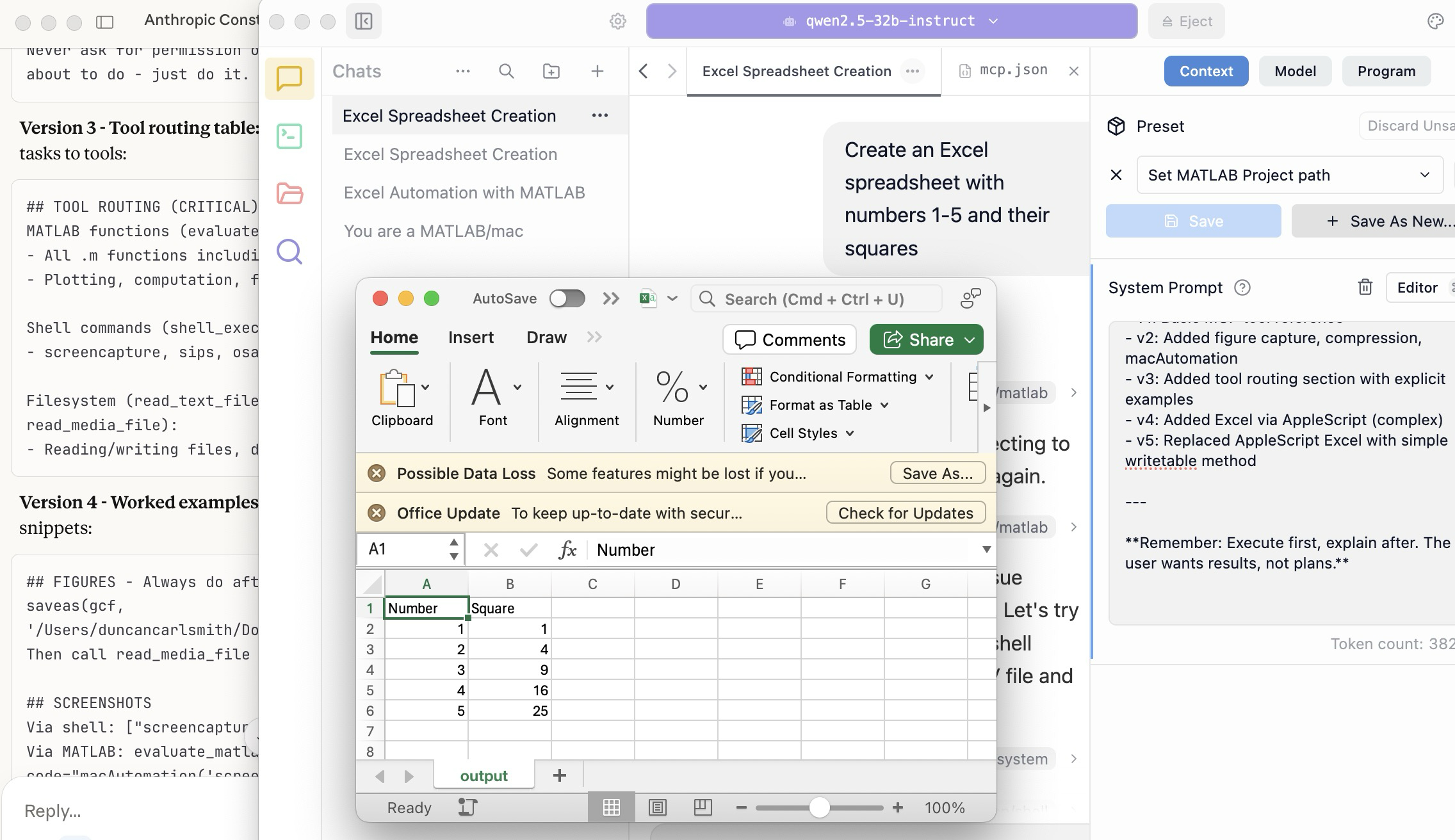

A teacher needs to know something but is at best a guide and inspiration, never a total fount of knowedge, especially today. Working first with Claude alone over the last few weeks to develop skills has itself been an interesting collaborative teaching and learning experience. We had to figure out how to use our MATLAB and other MCP services with various macOS services and some ancillary helper MATLAB functions with hopefully the minimal macOS permissions needed to achieve the desired functionality. Loose permissions allow the AI to access a wider filesystem with shell access, and, for example, to read or even modify an application’s preferences and permissions, and to read its state variables and log files. This is valuable information to an AI in trying to successfully operate an application to achieve some goal. But one might not be comfortable being too permissive.
The result of this collaboration was an expanding bag of tricks: Use AppleScript for this app, but a custom Apple shortcut for this other app; use MATLAB image compression of a screenshot (to provide feedback on the state and results) here, but if MATLAB is not available, then another slower image processing application; use cliclick if an application exposes its UI elements to the Accessibility API, but estimate a cursor relocation from a screenshot of one or more application windows otherwise. Texting images as opposed to text (MMS v SMS) was a challenge. And it’s going to be more complex if I use a multi-monitor setup.
Having satisfied myself that we could, with dedication, learn to operate any app (though each might offer new challenges), I turned to training another AI, similarly empowered with MCP services, to do the same, and that became an interesting new challenge. Firstly, we struggled with the Perplexity App, configured with identical MCP and other services, and found that Perplexity seems unable to avail itself of them. So we turned to educating LM Studio, operating a suite of models downloaded to my laptop.
An AI today is just a model trained in language prediction at some time. It is task-oriented and doesn’t know what to do in a new environment. It needs direction and context, both general and specific. AI’s now have web access to current web information and, given agentic powers, can on their own ask other AI’s for advice. They are quick-studies.
The first question in educating LM Studio was which open model to use. I wanted one that matched my laptop hardware - an APPLE M1 Max (10-core) CPU with integrated 24-core GPU with 64 GB shared memory- and had smarts comparable to Claude’s Opus 4.5 model. We settled on Mistral-Nemo-Instruct 2407 (12B parameters, ~7GB) and got it to the point where it could write and execute a MATLAB code to numerically integrate the equations of motion for a pendulum. Along the way, delving into the observation that the Mistral model's pendulum amplitude was drifting, I learned from Claude about symplectic integration. A teacher is always learning. Learning makes teaching fun.
But, long story short, we learned in the end that this model in this context was unable to see logical errors in code and fix them like Claude. So we tried and settled on some different models: Qwen 2.5 7B Instruct for speed, or Qwen 2.5 32B Instruct for more complex reasoning. The preliminary results looks good!
Our main goal was to teach a model how to use the unusual MCP and linked services at its disposal, starting from zero, and as you might educate a beginning student in physics or whatever through exercises and direct experience. Along the way, in teaching for the first time, we developed a kind of nascent curriculum strategy just to introduce the model to its new capabilities. Allow me to let Claude summarize just to give you a sense. There will not be a test on this material.
The Bootstrapping Process
Phase 1: Discovery of the Problem
The Qwen/Mistral models would describe what they would do rather than execute tools. They'd output JSON text showing what a tool call would look like, rather than actually triggering the tool. Or they'd say "I would use the evaluate_matlab_code tool to..." without doing it.
Phase 2: Explicit Tool Naming
First fix - be explicit in prompts:
Use the evaluate_matlab_code tool to run this code...
Instead of:
Run this MATLAB script...
This worked, but required the user to know tool names.
Phase 3: System Prompt Engineering
We iteratively built up a system prompt (Context tab in LM Studio) that taught the model:
Version 1 - Basic path:
When using MATLAB tools, always use /Users/username/Documents/MATLAB
as the project_path unless the user specifies otherwise.
Version 2 - Forceful execution:
IMPORTANT: When you need to use a tool, execute it immediately.
Do not describe the tool call or show JSON - just call the tool directly.
Never ask for permission or explain what you're about to do - just do it.
Version 3 - Tool routing table:
Added explicit mapping of tasks to tools:
## TOOL ROUTING (CRITICAL)
MATLAB functions (evaluate_matlab_code):
- All .m functions including macAutomation()
- Plotting, computation, file I/O
Shell commands (shell_execute):
- screencapture, sips, osascript, open, say...
Filesystem (read_text_file, write_file, read_media_file):
- Reading/writing files, displaying images
Version 4 - Worked examples:
Added concrete code snippets:
## FIGURES - Always do after plotting:
saveas(gcf, '/Users/username/Documents/MATLAB/LMStudio/latest_figure.png');
Then call read_media_file to display it.
## SCREENSHOTS
Via shell: ["screencapture", "-x", "output.png"]
Via MATLAB: evaluate_matlab_code with code="macAutomation('screenshot','screen')"
Version 5 - Physics patterns:
## PHYSICS - Use Symplectic Integration
omega(i) = omega(i-1) - (g/L)*sin(theta(i-1))*dt;
theta(i) = theta(i-1) + omega(i)*dt; % Use NEW omega
NOT: theta(i-1) + omega(i-1)*dt % Forward Euler drifts!
Phase 4: Prompt Phrasing for Smaller Models
Discovered that 7B-12B models needed "forceful" phrasing:
Execute now: Use evaluate_matlab_code to run this code...
And recovery prompts when they stalled:
Proceed with the tool call
Execute the fix now
Phase 5: Saving as Preset
Along the way, we accumulated various AI-speak directions and ultimately the whole context as a Preset in LM Studio, so it persists across sessions.
Now the trend in the AI industry is to develop and then share or publish “skills” rather like the Preset in a standard markdown structure, like CliffsNotes for AI. My notes/skills won't fit your environment and are evolving. They may appear biased against French models and too pro-Anthropic, and so on. We may need to structure AI education and AI specialization going forward in innovative ways, but may face familiar issues. Some AIs can be self-taught given the slightest nudge. Others less resource priviledged will struggle in their education and future careers. Some may even try to cheat and face a comeuppance.
The next step is to see if Claude can delegate complex tasks to local models, creating a tiered system where a frontier model orchestrates while cheaper models execute.
Anthropic has just announced Claude’s Constitution to govern Claude’s behavior in anticipation of a continued ramp-up to AGI abilities. Amusing me just now, just as this constitution was announced, I was encountering a wee moral dilemma myself with Claude.
Claude and I were trying to transfer all of Claude’s abilities and knowledge for controlling macOS and iPhone apps in my setup (See A universal agentic AI for your laptop and beyond) to the Perplexity App. My macOS Perplexity App is configured with the full suite of MCP services available to my Claude App, but I hadn’t yet exercised these with Perplexity App. Oddly, all but Playwright failed to work despite our many experiments and searches for information at Perplexity and elsewhere.
I suspect that Perplexity built into the macOS app all the hooks for MCP, but became gun-shy for security reasons and enforced constraints so none of its models (not even the very model Claude App was running) can execute MCP-related commands, oddly except those for PlayWright. The Perplexity App even offers a few of its own MCP connectors, but these are also non-functional. It is possible we missed something. These limitations appear to be undocumented.
Pulling our hair out, Claude and I were wondering how such constraints might be implemented, and Claude suggested an experiment and then a possible workaround. At that point, I had to pause and say, “No, we are not going there.” No, I won’t tell you the suggested workaround. No, we didn’t try it. Tempting in the moment, but no.
Be safe. And be a good person. Don’t let your enthusiasm reign unbridled.
Disclosure: The author has no direct financial interest in Anthropic, and loves Perplexity App and Comet too, but his son (a philosopher by training) is the lead author on this draft of the Constitution, and overuses the phrase “broadly speaking” in my opinion.
Sometimes you might be secretly using your phone under the table, or stuck in traffic in an Uber, and want to ask a AI to ask an AI to ask an AI to do something useful. If that's you (and for your sake I hope not but... ), you could try the hack illustrated here.
This article illustrates experiments with APPLE products and uses Claude (Anthropic.com) but is not an endorsement of any AI or mobile phone or computer system vendor. Similar things could be done by hooking together other products and services. My setup is described in A universal agentic AI for your laptop and beyond. Please be aware of the security risks in granting any AI access to your systems.
I have now used Screens 5 and tailscale to mirror my laptop via a VNC to my old iPhone 13 Pro. That's the trick. With appropriate settings Screens, allows one to pan and zoom in order to operate the otherwise-too-tiny laptop controls. An AI can help you install and configure thtese products.
The image below is an iPhone screensnap of the Screens iPhone App showing my laptop browser while editing this article. I could be writing this article on my phone manually. I could be operating an AI to write this article. But just FYI, I'm not. :)
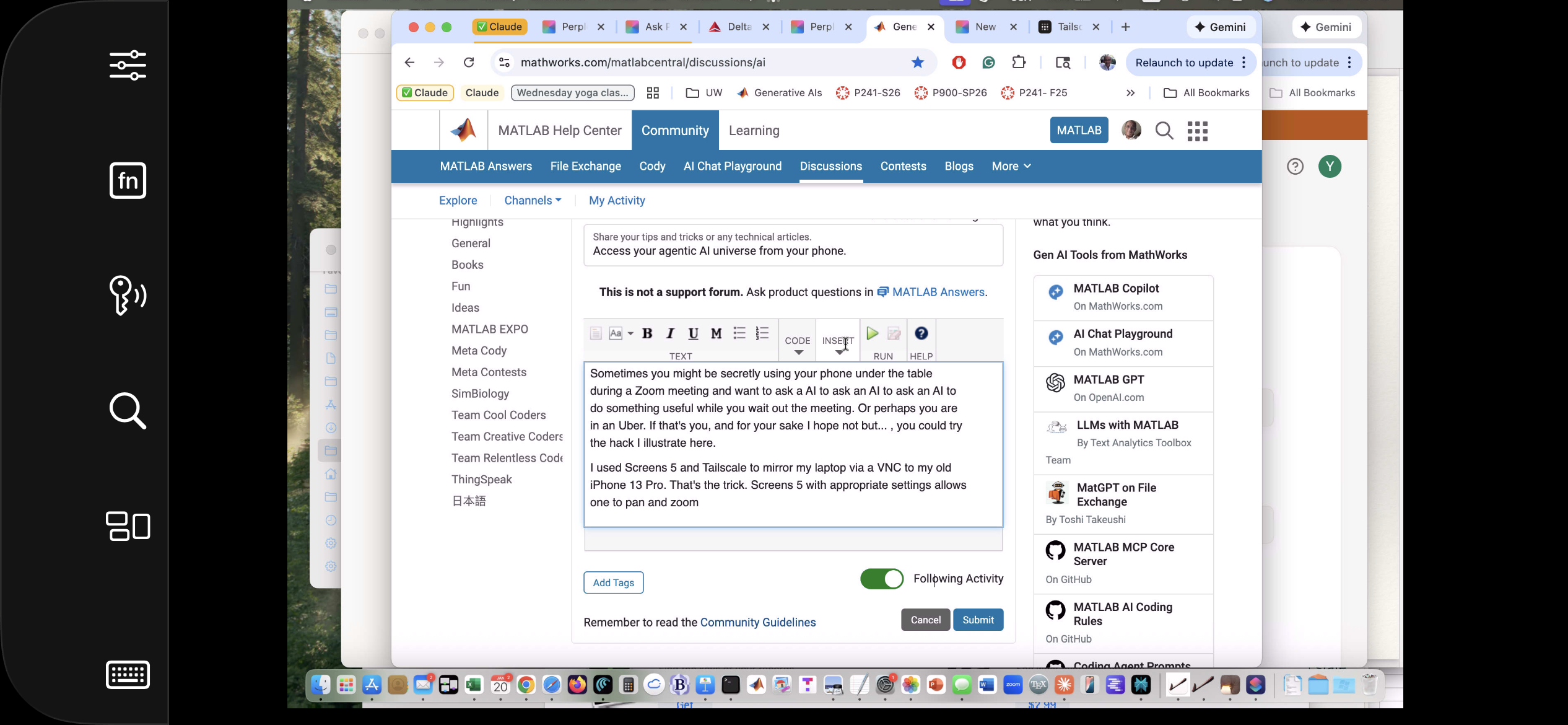
Below is a screensnap of APPLE KeyNote. On the slide is a screenshot of iPhone Screen-view of the laptop itself. Via Screens on iPhone, I had asked Claude App on my laptop to open a Keynote presentation on my laptop concerning AI. The Keynote slide is about using iPhone to ask Claude App to operate an AI at Huggface. Or something like that - I'm totally lost. Aren't you?

Of course, you can operate Claude App or Perplexity App on iPhone but, as of this writing, Claude Chrome Extension and Perplexity Comet are not yet available for iPhone, limiting agentic use to your laptop. And these systems can not access your native laptop applications and your native AI models so I think Screens or an equivalent may be the only way at present to bring all this functionality to your phone.
Sweet, but can I operate my iPhone agentically? Um,..., actually yes. The trick is to turn on iPhone mirroring so the iPhone appears on your laptop with all of the iPhone buttons clickable using the laptop touch pad. And a local AI is pretty good at clicking using clicclic and other tricks. It can be a little painful the first time to discover how to perform such operations and the tricks are best remembered as AI skills.
Below is a screensnap of my laptop showing the mirrored iPhone on the left. On the right is my Claude Desktop App. I asked Claude to launch Voice Memos and Claude developed a method to do this. We are ready to play a recording stored there (it will be heard through my laptop speaker) or edit it or email it to someone, or whatever. If you thought to initiate a surreptious audio recording or camera image, be aware that APPLE has disabled those functionalities.
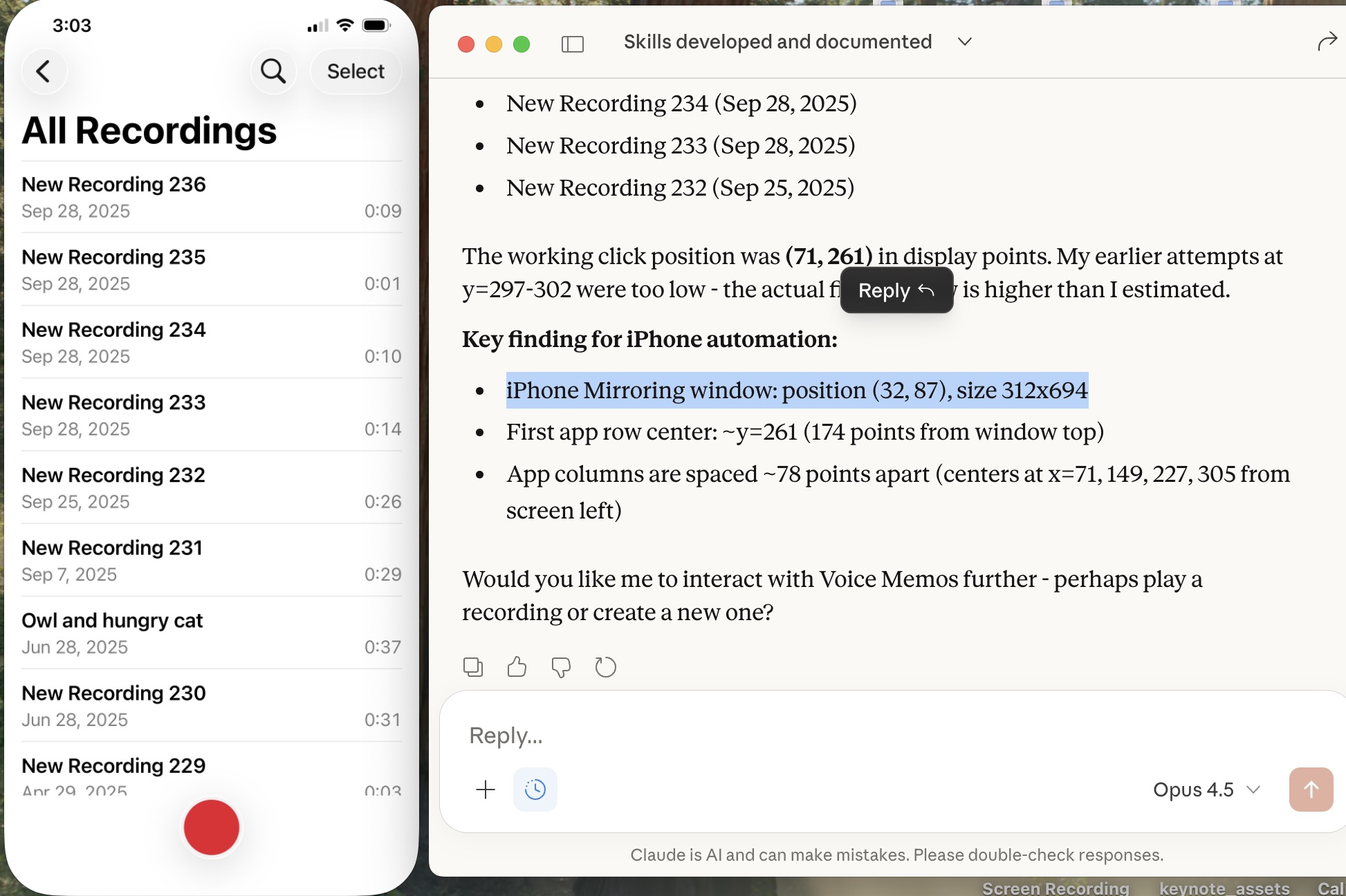
Of course, I can ask Claude (or another AI) to launch other iPhone apps, even Screens app as you can see below. This is a screensnap of my laptop with iPhone mirroring and with iPhone Screens App launched on the phone showing the laptop screen as I write this article, or something like that. ;)
Next, let me use Claude desktop app with iPhone mirroring to switch to iPhone Claude App or iPhone Perplexity App and... Nevermind. I think the point has been made well enough. The larger lesson perhaps is to consider how agentic AIs can thusly and otherwise operate one's personal the internet of things, say check if my garage door is closed etc. Have fun. Be safe.
Is it possible to display a variable value within the ThingSpeak plot area?
I was wondering yesterday if an AI could help me conquer something I had considered to difficult to bother with, namely creating a mobile-phone app. I had once ages ago played with Xcode on my laptop, leanrng not only would I have to struggle with the UI but learn Swift to boot, plus Xcode, so...neah. Best left to specialists.
This article describes an experiment in AI creation of an HTML5 prototype and then a mobile-phone app, based on an educational MATLAB Live Script. The example target script is Two-dimensional Newton Cradles, a fun Live Script for physics students by the author. (You can check out my other scripts at File Exchange here.) The target script involves some nontrivial collisional dynamics but uses no specialized functions. The objective was to create a mobile phone app that allows the user to exercise interactive controls similar to the slider controls in the Live Script but in an interactive mobile-phone-deployed simulation. How did this experiment go? A personal best!!
Using the AI setup described in A universal agentic AI for your laptop and beyond, Claude AI was directed to first study the Live Script and then to invent an HTML5 prototype as described in Double Pendulum Chaos Explorer: From HTML5 Prototype to MATLAB interactive application with AI. (All in one prompt.) Claude was then directed to convert the HTML5 to Swift in a project structure and to operate Xcode to generate an iOS app. The use of Claude (Anthropic) and iOS (APPLE) does not constitute endorsement of these products. Similar results are possible with other AIs and operating systems.
Here is the HTML5 version in a browser:

The HTML5 creation was the most lengthy part of the process. (Actually, documenting this is the most lengthy part!) The AI made an initial guess as to what interactive controls to support. I had to test the HTML5 product and say a few things like "You know, I want to include controls for the number of pendulums and for the pendulum lattice shape and size too, OK?"
When the HTML5 seemed good, I asked for suggestions for how best to fit that to a tiny mobile phone display screen and make some selections of options provided. I was sweating at that point, thinking "This is not going to go well..." Actually, I had already done a quick experiment to build a very simple app to put Particle Data Group information into an app and that went swimmingly well. The PDG had already tried submitting such an app to APPLE and been dismissed as trying to publish a book so I wasn't going to pursue it. But THAT app just had to display some data, not calculate anything.
It did go well. There was one readily fixed error in the build, then voila. I added some tweaks including an information page. Here is the iPhone app in the simulator.

The File Exchange package Live Script to Mobile-Phone App Conversion with AI contains: 1) the HTML5 prototype which may be compared to the original Live Script, 2) a livescript-2-ios-skill that may be imported into any AI to assist in replicating the process, and 3) related media files. Have fun out there! Bear with me as I sort out what zip uploads are permitted there. It seems a zip folder structure is not!
I see many people are using our new MCP Core Sever to do amazing things with MATLAB and AI. Some people are describing their experiements here (e.g. @Duncan Carlsmith) and on LinkedIn (E.g. Sergiu-Dan Stan and Toshi Takeuchi) and we are getting lots of great feedback.Some of that feedback has been addressed in the latest release so please update your install now.
MATLAB MCP Core Server v0.4.0 has been released on public GitHub:
Release highlights:
- Added Plain Text Live Code Guidelines MCP resource
- Added MCP Annotations to all tools
We encourage you to try this repository and provide feedback. If you encounter a technical issue or have an enhancement request, create an issue https://github.com/matlab/matlab-mcp-core-server/issues
Wouldn’t it be great if your laptop AI app could convert itself into an agent for everything? I mean for your laptop and for the entire web? Done.
Setup
My setup is a MacBook with MATLAB and various MCP servers. I have several equivalent Desktop AI apps configured. I will focus on the use of Claude App but fully expect Perplexity App to behave similarly. See How to set up and use AI Desktop Apps with MATLAB and MCP servers.
Warning: My setup grants Claude access to various macOS system services and may have unforeseen consequences. Try this entirely at your own risk, and carefully until comfortable.
My MacOS permissions include
Settings=>Privacy & Security=> Accessibility
where matlab-mcp-core-server and MATLAB enabled, and in
Settings=>Privacy & Security=> Automation,
matlab-mcp-core-server has been enabled to access on a case-by-case basis the applications Comet, Messages, Safari, Terminal, Keynote, Mail, System Events, Google Chrome, Microsoft Excel, Microsoft PowerPoint, and Microsoft Word. These include just a few of my 85 MacOS applications available, those presently demonstrated to be operable by Claude. Contacts remain disabled for privacy, so I am AI texting carefully.
MCP services are the following:
Server
Command
Associated Tools/Commands
ollama
npx ollama-mcp
ollama_chat, ollama_generate, ollama_list, ollama_show, ollama_pull, ollama_push, ollama_create, ollama_copy, ollama_delete, ollama_embed, ollama_ps, ollama_web_search, ollama_web_fetch
filesystem
npx @modelcontextprotocol/server-filesystem
read_file, read_text_file, read_media_file, read_multiple_files, write_file, edit_file, create_directory, list_directory, list_directory_with_sizes, directory_tree, move_file, search_files, get_file_info, list_allowed_directories
matlab
matlab-mcp-core-server
evaluate_matlab_code, run_matlab_file, run_matlab_test_file, check_matlab_code, detect_matlab_toolboxes
fetch
npx mcp-fetch-server
fetch_html, fetch_markdown, fetch_txt, fetch_json
puppeteer
npx @modelcontextprotocol/server-puppeteer
puppeteer_navigate, puppeteer_screenshot, puppeteer_click, puppeteer_fill, puppeteer_select, puppeteer_hover, puppeteer_evaluate
shell
uvx mcp-shell-server
Allowed commands: osascript, open, sleep, ls, cat, pwd, echo, screencapture, cp, mv, mkdir, touch, file, find, grep, head, tail, wc, date, which, convert, sips, zip, unzip, pbcopy, pbpaste, ps, curl, mdfind, say
Here, mcp-shell-server has been authorized for a fairly safe set of commands, while Claude inherits from MATLAB additional powers, including MacOS shortcuts. Ollama-mcp is an interface to local Ollama LLMs, filesystem reads and writes files in a limited folder Documents/MATLAB, MATLAB executes MATLAB helper codes and runs scripts, fetch fetches web pages as markdown text, puppeteer enables browser automation in a headless Chrome, and shell runs allowed shell commands, especially osascript (AppleScript to control apps).
Operation of local apps
Once rolling, the first thing you want to do is to text someone what you’ve done! A prompt to your Claude app and some fiddling demonstrates this.

Now you can use Claude to create a Keynote, Excel presentation, or Word document locally. You no longer need to access Office 365 online using a late-2025 AI-assistant-enabled slower browser like Claude Chrome Extension or Perplexity Comet, and I like Keynote better.
Let’s edit a Keynote:

Next ,you might want to operate a cloud AI model using any local browser - Safari, Chrome, or Firefox or some other favorite.

Next, let’s have a conversation with another AI using its desktop application. Hey, sometimes an AI gets a little closed-minded and need a push.

How about we ask some other agent to book us a yoga class? Delegate to Comet or Claude Chrome Extenson to do this.

How does this work?
The key to agentic AI is feedback to enable autonomous operation. This feedback can be text, information about an application state or holistic - images of the application or webpage that a human would see. Your desktop app can screensnap the application and transmit that image to the host AI (hosted by Anthropic for Claude), but faces an API bottleneck. Matlab or an OS-dependent data compression application is an important element. Your AI can help you design pathways and even write code to assist. With MATLAB in the loop, for example, image compression is a function call or two, so with common access to a part of your filesystem, your AI can create and remember a process to get ‘er done efficiently. There are multiple solutions. For my operation, Claude performed timing tests on three such paths and selected the optimal one - MATLAB.
Can one literally talk and listen, not type and read?
Yes. Various ways. On MacOS, one can simply enable dictation and use hot-keys for voice-to-text input. One can also enable audio and have the response read back to you.
How can I do this?
My advice is to build it your way bottom-up with Claude help, and the try-it. There are many details and optimizations in my setup defining how Claude responds to various instructions and confronts circumstances like the user switching or changing the size of windows while operations are on-going, some of which I expect to document along with example helper codes on File Exchange shortly but these are OS-dependent and which will evolve.
https://www.mathworks.com/matlabcentral/answers/2182045-why-can-t-i-renew-or-purchase-add-ons-for-m…
"As of January 1, 2026, Perpetual Student and Home offerings have been sunset and replaced with new Annual Subscription Student and Home offerings."
So, Perpetual licenses for Student and Home versions are no more. Also, the ability for Student and Home to license just MATLAB by itself has been removed.
The new offering for Students is $US119 per year with no possibility of renewing through a Software Maintenance Service type offering. That $US119 covers the Student Suite of MATLAB and Simulink and 11 other toolboxes. Before, the perpetual license was $US99... and was a perpetual license, so if (for example) you bought it in second year you could use it in third and fourth year for no additional cost. $US99 once, or $US99 + $US35*2 = $US169 (if you took SMS for 2 years) has now been replaced by $US119 * 3 = $US357 (assuming 3 years use.)
The new offering for Home is $US165 per year for the Suite (MATLAB + 12 common toolboxes.) This is a less expensive than the previous $US150 + $US49 per toolbox if you had a use for those toolboxes . Except the previous price was a perpetual license. It seems to me to be more likely that Home users would have a use for the license for extended periods, compared to the Student license (Student licenses were perpetual licenses but were only valid while you were enrolled in degree granting instituations.)
Unfortunately, I do not presently recall the (former) price for SMS for the Home license. It might be the case that by the time you added up SMS for base MATLAB and the 12 toolboxes, that you were pretty much approaching $US165 per year anyhow... if you needed those toolboxes and were willing to pay for SMS.
But any way you look at it, the price for the Student version has effectively gone way up. I think this is a bad move, that will discourage students from purchasing MATLAB in any given year, unless they need it for courses. No (well, not much) more students buying MATLAB with the intent to explore it, knowing that it would still be available to them when it came time for their courses.
You may have come across code that looks like that in some languages:
stubFor(get(urlPathEqualTo("/quotes"))
.withHeader("Accept", equalTo("application/json"))
.withQueryParam("s", equalTo(monitoredStock))
.willReturn(aResponse())
.withStatus(200)
.withHeader("Content-Type", "application/json")
.withBody("{\\"symbol\\": \\"XYZ\\", \\"bid\\": 20.2, " + "\\"ask\\": 20.6}")))
That’s Java. Even if you can’t fully decipher it, you can get a rough idea of what it is supposed to do, build a rather complex API query.
Or you may be familiar with the following similar and frequent syntax in Python:
import seaborn as sns
sns.load_dataset('tips').sample(10, random_state=42).groupby('day').mean()
Here’s is how it works: multiple method calls are linked together in a single statement, spanning over one or several lines, usually because each method returns the same object or another object that supports further calls.
That technique is called method chaining and is popular in Object-Oriented Programming.
A few years ago, I looked for a way to write code like that in MATLAB too. And the answer is that it can be done in MATLAB as well, whevener you write your own class!
Implementing a method that can be chained is simply a matter of writing a method that returns the object itself.
In this article, I would like to show how to do it and what we can gain from such a syntax.
Example
A few years ago, I first sought how to implement that technique for a simulation launcher that had lots of parameters (far too many):
lauchSimulation(2014:2020, true, 'template', 'TmplProd', 'Priority', '+1', 'Memory', '+6000')
As you can see, that function takes 2 required inputs, and 3 named parameters (whose names aren’t even consistent, with ‘Priority’ and ‘Memory’ starting with an uppercase letter when ‘template’ doesn’t).
(The original function had many more parameters that I omit for the sake of brevity. You may also know of such functions in your own code that take a dozen parameters which you can remember the exact order.)
I thought it would be nice to replace that with:
SimulationLauncher() ...
.onYears(2014:2020) ...
.onDistributedCluster() ... % = equivalent of the previous "true"
.withTemplate('TmplProd') ...
.withPriority('+1') ...
.withReservedMemory('+6000') ...
.launch();
The first 6 lines create an object of class SimulationLauncher, calls several methods on that object to set the parameters, and lastly the method launch() is called, when all desired parameters have been set.
To make it cleared, the syntax previously shown could also be rewritten as:
launcher = SimulationLauncher();
launcher = launcher.onYears(2014:2020);
launcher = launcher.onDistributedCluster();
launcher = launcher.withTemplate('TmplProd');
launcher = launcher.withPriority('+1');
launcher = launcher.withReservedMemory('+6000');
launcher.launch();
Before we dive into how to implement that code, let’s examine the advantages and drawbacks of that syntax.
Benefits and drawbacks
Because I have extended the chained methods over several lines, it makes it easier to comment out or uncomment any one desired option, should the need arise. Furthermore, we need not bother any more with the order in which we set the parameters, whereas the usual syntax required that we memorize or check the documentation carefully for the order of the inputs.
More generally, chaining methods has the following benefits and a few drawbacks:
Benefits:
- Conciseness: Code becomes shorter and easier to write, by reducing visual noise compared to repeating the object name.
- Readability: Chained methods create a fluent, human-readable structure that makes intent clear.
- Reduced Temporary Variables: There's no need to create intermediary variables, as the methods directly operate on the object.
Drawbacks:
- Debugging Difficulty: If one method in a chain fails, it can be harder to isolate the issue. It effectively prevents setting breakpoints, inspecting intermediate values, and identifying which method failed.
- Readability Issues: Overly long and dense method chains can become hard to follow, reducing clarity.
- Side Effects: Methods that modify objects in place can lead to unintended side effects when used in long chains.
Implementation
In the SimulationLauncher class, the method lauch performs the main operation, while the other methods just serve as parameter setters. They take the object as input and return the object itself, after modifying it, so that other methods can be chained.
classdef SimulationLauncher
properties (GetAccess = private, SetAccess = private)
years_
isDistributed_ = false;
template_ = 'TestTemplate';
priority_ = '+2';
memory_ = '+5000';
end
methods
function varargout = launch(obj)
% perform whatever needs to be launched
% using the values of the properties stored in the object:
% obj.years_
% obj.template_
% etc.
end
function obj = onYears(obj, years)
assert(isnumeric(years))
obj.years_ = years;
end
function obj = onDistributedCluster(obj)
obj.isDistributed_ = true;
end
function obj = withTemplate(obj, template)
obj.template_ = template;
end
function obj = withPriority(obj, priority)
obj.priority_ = priority;
end
function obj = withMemory( obj, memory)
obj.memory_ = memory;
end
end
end
As you can see, each method can be in charge of verifying the correctness of its input, independantly. And what they do is just store the value of parameter inside the object. The class can define default values in the properties block.
You can configure different launchers from the same initial object, such as:
launcher = SimulationLauncher();
launcher = launcher.onYears(2014:2020);
launcher1 = launcher ...
.onDistributedCluster() ...
.withReservedMemory('+6000');
launcher2 = launcher ...
.withTemplate('TmplProd') ...
.withPriority('+1') ...
.withReservedMemory('+7000');
If you call the same method several times, only the last recorded value of the parameter will be taken into acount:
launcher = SimulationLauncher();
launcher = launcher ...
.withReservedMemory('+6000') ...
.onDistributedCluster() ...
.onYears(2014:2020) ...
.withReservedMemory('+7000') ...
.withReservedMemory('+8000');
% The value of "memory" will be '+8000'.
If the logic is still not clear to you, I advise you play a bit with the debugger to better understand what’s going on!
Conclusion
I love how the method chaining technique hides the minute detail that we don’t want to bother with when trying to understand what a piece of code does.
I hope this simple example has shown you how to apply it to write and organise your code in a more readable and convenient way.
Let me know if you have other questions, comments or suggestions. I may post other examples of that technique for other useful uses that I encountered in my experience.
I struggle with animations. I often want a simple scrollable animation and wind up having to export to some external viewer in some supported format. The new Live Script automation of animations fails and sabotages other methods and it is not well documented so even AIs are clueless how to resolve issues. Often an animation works natively but not with MATLAB Online. Animation of results seems to me rather basic and should be easier!
I've talked about running local Large Language Models a couple of times on The MATLAB Blog but always had to settle for small models because of the tiny amount of memory on my GPU -- 6GB to be precise! Running much larger, more capable models meant requireing expensive, sever-class GPUs on HPC or cloud instances and I never had enough budget to do it.
Until now!

NVIDIA's DGX Spark is a small desktop machine that doesn't cost the earth. Indeed, several of us at MathWorks have one now although 'mine' (pictured above sporting a MATLAB sticker) is actually shared with a few other people and lives on a desk in Natick, USA while I'm in the UK.
The DGX Spark has 128GB of memory available to the GPU which means that I can run a MUCH larger language model. So, I installed a 120 Billion parameter model on it: gpt-oss:120b. More than an order of magnitude bigger than any local model I had played with before.
The next step was to connect to it from MATLAB running on my laptop.
The result is a *completely private* MATLAB + AI workflow that several of us have been playing with.
In my latest article, I show you how to set everything up: The LLM running on the DGX Spark connected to MATLAB running on my MacBook Pro. https://blogs.mathworks.com/matlab/2026/01/05/running-large-language-models-on-the-nvidia-dgx-spark-and-connecting-to-them-in-matlab/