Designing Battery Systems with Modeling and Simulation

So my name is Javier. I have been with The MathWorks for about nine years now. And most of what I do at The MathWorks has to do with modeling battery systems.

So as I was saying before, most of what I do at The MathWorks has to do with one of the most important energy devices that allow us to do many of the things that we can do in modern times and then, of course, talking about the battery.

Battery is something that it's everywhere. It's in cell phones. It's in cars. It's in laptops, in all kinds of mobile and stationary devices. And it allows us to do a great number of things, from working to traveling to communicating with one another and many, many very cool applications of batteries.

The most popular and commonly seen battery nowadays-- and it's the case with the batteries inside all of these devices that you are seeing here-- is the lithium ion battery. Now lithium ion batteries are very popular. They have a very good energy density. They are very light. They are very powerful. You can cycle them. And they are excellent as long as we keep them within the operating range that they have been designed for.

And that to help rating range has to be followed. And we need to very carefully manage the battery so that its operating state doesn't go outside of the safety limits, or you know that bad things can happen.

So there is a lot of energy inside lithium ion battery cells. And there's potential problems in not managing the operation of the battery correctly. There's flammable materials inside, and the cases that I am exemplifying here can very quickly go all over the news.

So what do we have to take care of when we manage a battery? Well, there's a few things that designing battery systems require. One of them is that we need to take very carefully into consideration that the temperature dependency of the battery behavior.

Battery behaves differently when it is cold versus when it is warm or clot. So the physical phenomena inside the battery are in general thermally activated, which means that they are, in general, exponentially dependent on temperature. And that's something that has very, very important practical implications.

You may know that an electric vehicle range is significantly reduced in cold temperature. And the reason for that is that the discharge capacity of the battery cell is reduced because of the increasing internal resistance at low temperature, meaning that the voltage cutoff is reached before the battery is fully drained. So that's one of the aspects that we need to take into consideration when we design battery systems and also models for batteries.

On the other side of the spectrum, an elevated operating temperature is also not desirable for, first, degradation reasons. The battery will degrade faster at warmer temperatures. And also when the temperature exceeds a certain threshold, things become dangerous, and the battery can develop a thermal event. So that's another aspect that we need to take into consideration.

And the third one associated with the temperature is that charging is one of the most delicate procedures in lithium ion cells, and we need to, for example, avoid charging a battery below 0 degrees Celsius. That's very important as well. Most lithium ion batteries behave like that.

The second aspect to consider here is the state of charge, so the amount of energy that is available for us to extract from the battery. The state of charge indicates how much longer we will be able to use our cell phone or a laptop and also how much longer we'll be able to drive our electric vehicle.

So it is, of course, very important to have a good estimate for that, in particular, when we're talking about electric vehicles because not knowing how much longer we will be able to drive is what in English is referred to as “range anxiety”, so not much knowing how much longer we'll be able to drive our car.

The problem with state of charge determination is that state of charge is not something that we can measure directly. Unlike what happens with the level of fuel in a conventional vehicle, I cannot look into the battery cell as I can look into bucket of water and see how much water is inside.

With state of charge, what we have to do is measure something else and with the model of the battery estimate the state of charge. And the models can become fairly sophisticated. And we will see a couple of them during the course of this morning.

Number three, degradation or aging. It's also a very well-known fact for all batteries, but lithium ion batteries in particular, that they don't behave the same when they are new versus when they have undergone a certain number of cycles. Degradation effects performance. The internal resistance goes up, meaning that the power that I can extract from my battery is not the same as it was when the battery was new.

The capacity goes down in a phenomenon called capacity fade because of the internal degradation of the battery component materials that can now no longer hold the same number of lithium ions in their lattice. So both power and energy become compromised. And there are many aspects of the operation of the battery cell that affect the rate at which it degrades.

So driving the electric vehicle more aggressively is going to accelerate degradation. Driving it at extreme temperatures, be it cold or hot, same thing. The frequency of recharging and the average depth of the discharge is also going to affect the rate at which the battery will degrade.

And what is challenging about understanding degradation is that it is very difficult to put together a comprehensive model that allows us to understand and predict the rate at which the battery is going to degrade. Nobody really knows exactly the way in which all of the environmental conditions and operating conditions are going to combine in order to get a certain degradation right.

So what ends up happening is that that lack of understanding of the physical processes, what it means is that the battery engineer will have to oversize or over-engineer the battery pack in order to account for that degradation to occur within the warranty period.

In automotive, a capacity fade up to 20% is considered the final state of the battery in terms of health. So when it can no longer hold 80% of the charge for which it had been designed to, that battery is considered gone. So very, very stringent requirements there.

So what do we do to tackle all of these challenges to design battery systems using models? And one of the things that I want to answer with this conversation that we are having is ultimately, why do we need models of the battery? And what's the use of having a good model of the battery?

So the modeling approach that we take is a system-level approach that aims at providing us a means for system-level simulation for control design. So we want to model a battery so that we can scale that model up through a module of a few tens of unit battery cells and even to a pack with a few hundred of cells.

And the equivalent circuit, which is what you are seeing on the screen at this moment, is a good way to create a useful model of the battery that is scalable. An equivalent circuit-- we will see this in more detail later-- but it has a voltage source. It has an internal resistance. And it has a few other components that give the battery cell its time-dependent behavior.

And during the first part of our conversation today, we are going to see how to create a good equivalent circuit model of the unit cell so that we can reproduce in a simulation real life behavior of a certain cell chemistry for which we will use a combination of simulation and characterization experience.

So that is going to be point number one of today's discussion, how to characterize a battery cell. Let's say that you are an OEM, and you need to energize your electric vehicle with a battery pack. And you want to, first of all, decide what kind of battery chemistry to use. So once you have decided that, you have a few cells that you can test. And you want to create a model of that cell in order to do your BMS design. So how do we go about doing that?

We will also see a convenient way of using physical modeling to scale-up the battery cell to a module and a pack. And this is going to be useful for things such as battery cell balancing, thermal management, and things of that sort.

The third topic will be state estimation. And we will talk about estimating the state of charge as we started saying before. And also I'll give you an idea of how we can estimate, using the same technique a bit modified, the state of health, so the level of degradation that the cell is experiencing.

After the break, we will start talking about the controller part-- the algorithm for battery management, which will, for example, give us algorithm architecture to put the system in default condition and manage when to balance and do a recharge contactor closing sequence, estimating or implementing the state of charge estimation and so on.

And the last topic will be an example of how to use statistical analysis for state of charge estimation. And we can also discuss an extension of that idea for SOH or State of Health estimation. So, point number five here is the one that doesn't have anything to do with simulation. You will be training a neural network to understand patterns of battery cell behavior in order to estimate the state of charge in a different way from the traditional ones.

So let's start with the construction of the equivalent circuit model of a unit cell, for which we will use a library in Simulink for a physical model. And so when we want to model a dynamic system, like the one that you are seeing here, traditionally, what we can do is write the mathematical equation that governs the behavior of the dynamic system and put together a Simulink model that comprises integrators, gains, sources, and addition blocks in order to integrate this equation here.

It's not necessary for me to go in detail explaining what this does. But just think about it in these terms. This is a second order ordinary differential equation. This is the acceleration. This is the velocity. And this is the displacement. And if what it wants to calculate is the displacement as a function of time, what I can do is say, well, force minus these two terms-- which are the ones that I am subtracting from here-- divided by the mass gives me the acceleration. And then if I integrate the acceleration twice, I get displacement on the opposite end.

So the idea that I want to convey with this example is that when we are using Simulink to generate a model for a dynamic system like this one here, we need to go through the mathematical representation of the system and put together a Simulink model to solve that equation.

Physical modeling is a library on top of Simulink that brings to the table the functionality to do the same thing but without the math. So these are components of a library called Scenescape that works on top of Simulink such as all of these blocks-- the same way as these blocks. But they don't have a mathematical notion. They have a physical notion.

You can see that the connections are different. The elements are different. They represent physical entities. This way of modeling is called causal modeling because there is a cause and there's an effect. And there said directionality, that the information flows from left to right in here.

This one here is called acausal modeling or physical network-based modeling. And one of the characteristics that it has is that, well, first of all, I don't have to worry too much about the mathematics underlying the behavior of this system.

But there's also a very important implication of this way of modeling physical systems, which is the one that we can think of if we want to extend our design. Let's say that from one degree of freedom, we want to extend it to two degrees of freedom-- two degrees of freedom. So two masses connected to one another by springs and masses.

If I am working just with Simulink, what I do is we do the mathematical derivation, and we construct the Simulink model. And it becomes a little more complicated than before. But if I'm using physical modeling tools, the modification that I need to do is to go from here to here.

So you can see that among the other advantages, the model itself looks a lot like a drawing of the physical system itself. The same thing applies to electrical systems. So this first order filter can be represented by this transfer function. If I add a second loop to it, the transfer function plus the rest of the blocks become quite a bit more complicated. But if I'm using physical modeling tools, we can go this way and this way, so much more intuitive way of dealing with a physical system.

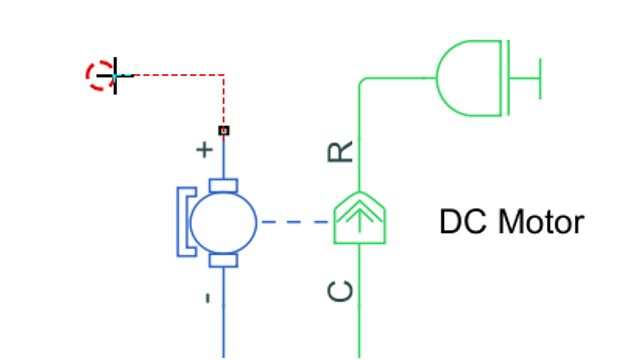
What does all these concepts have to do with battery cell modeling? Well, the equivalent circuit is an electrothermal analogy of the behavior of the cell that aims at representing the very complex electrochemical phenomena with something relatively easy to understand that is an equivalent circuit.

So what do I observe when I measure something out of a cell? Well, I have a, for sure, a voltage, an electromotive force or open circuit voltage. I have an internal resistance that causes the voltage to drop when I load my battery. And there's a few RC components connected in series with everything else that are a representation for the diffusion of phenomena inside the lithium ion battery that gifts the battery it's time-dependent behavior.

And that's why when you switch the battery state from polarized to current equal to 0, the voltage doesn't recover instantaneously, but it recovers exponentially with time. And the time constant of that exponential is given by the values of these capacitors and resistors. So we'll see how to use that in a battery cell.

So enough PowerPoint for the time being. Let's work with MATLAB and Simulink for now. So this one here will partially answer the NMC versus LFP first question in there. So what am I doing here? Well, by the way, this a Simulink model where I have a combination of traditional Simulink blocks, the ones that I showed at the beginning when I was describing this as causal modeling, so cause and effect, so all of the components having a mathematical notion and being linked by arrows that represent the flow of a signal.

And on the right-hand side, a very simple model of a short battery packet. Well, in battery technology, we call it 3S1P battery pack, so three cells in series, one two parallel. And what I am doing to this battery pack that is inside here-- and we will see it in a second-- is I am charging and discharging it. So let's take a look at the results, and we will explain what they mean and at the same time see what their relationship between that and the structure of the battery pack is.

So this is a battery pack that comprises three NMC 31 hand power pouch cells made by Kokam, the Korean manufacturer that we characterized several years ago. And my second example, my second demo will deal with how we did that characterization. But we will see in the parameters of this battery cell why this is an NMC cell like our colleague was asking us a minute ago.

So what am I doing with this cell? Well, I am charging and discharging it. So let's take a look at the voltage and current. My convention is that positive current is charge, and negative current is discharge. Half of my customers use the inverse convention. But that's OK. It doesn't matter. So I'm just telling you what the convention is so that what you're seeing becomes more clear.

So typically, the way we charge a lithium ion cell is with a protocol called CCCV, which means Constant Current, Constant Voltage. And there's several reasons why we do that. They have to do with charging as fast as possible but without risking overcharging the battery cell, which is very, very important.

And you can see that this is the constant current period. I am charging at about 15 amps, which means that I am charging at what battery engineers would call C/2. So if the battery is a 30 amp-hour battery charging at 30 amps is 1c. Charging it at 15 amps is C/2. The voltage is going up. And at a certain point, when the voltage reaches a certain level, I switch to voltage control. So I keep the voltage constant, and I let the current die out. And there is a convention saying, well, if the current is less than a certain level, I consider my battery pack fully charged.

There's another thing in here that is interesting to see. So, this is the state of charge. State of charge is the number between 0 and 1 that tells me how much charge there is inside the battery. And the state of charge is going up and down because I'm charging and discharging, of course.

But you can see that in addition to that, the initial states of charge are not only low, they are also different from one another. And what this is is a phenomenon called imbalance. So the cell, the cells or the battery pack cells, they start out of balance. And one of the things that I need to do as part of battery management is to bring them back in balance.

The reason for that is that it is extremely important never to overcharge a battery cell. So if the batteries are at different states of charge as I charge them, as soon as the state of charge of the cell that is at the top reaches the maximum value, I have to stop the charge because otherwise if I keep going, the cell that is at the top is going to overcharge. And that is very dangerous.

So what happens is the cells that are at the bottom never get fully charged. And the implication of that is that I am underutilizing my battery pack. So from time to time, I need to do what is called cell balancing. And in a minute, we will see how we do that in our model.

The third thing that is important and interesting to see here is the temperature evolution. So these are the three individual temperatures of the three cells that are inside this battery pack. We start the simulation at 20 degrees Celsius. And as we charge and discharge, the temperature goes up and down.

This maximum temperature is about 33 degrees Celsius. And it is not a concern in terms of safety. It is OK to run a battery cell at that temperature. What is, indeed, a concern is the difference between the minimum and the maximum. So this discrepancy, this difference is something that I need to avoid.

And the reason is because, as I was saying at the beginning, because the degradation, the aging of the cell is extremely temperature dependent. A few hundred cycles or a few months after using a cell in this way, this cell is going to degrade much faster than this one here.

So the individual battery cells in the pack are going to become more and more different from one another. And that will make the imbalance even worse. So that's why with a combination of good mechanical layout and thermal management, we have to avoid this temperature discrepancy. To give you an idea, between 5 and 8 degrees Celsius is the ballpark temperature difference that battery engineers have in mind as an objective. So more than that is something that we need to avoid.

So why is this happening? Well, let's take a look at the battery pack inside that subsystem. On the left-hand side, there's the plant. On the right-hand side is the very simple controller. So again, seeing the benefits of using physical modeling here, you can see that the model itself looks very much like a schematic of the physical system.

So three cells in series, so we have the 3S connection in here. There's no cells in parallel. And there's one more thing that is new at this point, and it is the fact that there's two different colors combined in the physical model of the cell, blue and orange.

Blue indicates electrical domain. Orange indicates thermal domain. So here, what we're doing is we're capturing both the electrical and the thermal phenomena that happen here. And in particular, the thermal effects are modeled with these components that are connected in-between cells that represent heat transfer by convection between cells 1, 2, and 3.

If we take a look at the way in which I created this small module, you can see that it's a pretty bad design in terms of thermal management because I am not doing any active cooling here. So whatever heat is developed by the flow of the current inside is not going anywhere but either being transferred in-between cells or going out to the atmosphere on this side.

But look at what's happened here. So I deliberately designed this in the wrong way in order to show the use of a tool like this that gives me this kind of undesirable behavior. So what's going on here is that this cell, cell number 3, is insulated on one side. So what that is causing is that the heat that is produced by this cell cannot go anywhere but towards the other cell by convection. And it cannot escape to the outside on the other side of the pack. And that is the reason why we can see that the temperature of cell number 3 is, on average, higher than the temperature of cells 1 and 2.

And cell number 1 is, by the way, thermally connected directly to the atmosphere. So we can evacuate the-- we can get rid of the heat that is generated by the flow of the current. And that's why its temperature is on average lower. So this is a design that needs some modification. It needs some active thermal management, some cooling, which I'm not implementing here. The rest of them all, the rest of the plant model, the components that are on the right-hand side are responsible for the balancing that I was talking about before.

So what is balancing? Well, balancing is bringing the states of charge together. So there's two main ways of doing that, namely passive balancing or active balancing. Passive balancing is the one that we are doing here. It's about determining which cells are where with respect to the other cells in terms of the state of charge. And the one that is at the top, we very slowly drain with a bleed resistor in here, allowing the other cells to catch up.

This is an, energetically speaking, in general, a bad idea because what we're doing is basically throwing away energy that we could otherwise use for something useful. But the alternative, which is active balancing, which means that cells that are higher in state of charge, charge other cells that are lower in state of charge.

But the problem with that is that even though it is conceptually more efficient, it is extremely expensive in terms of hardware because you need many, many MOSFETs per cell, at least three MOSFETs per cell, and one intermediate oscillator that is used to

Shuttle the energy from one cell to the other. So as far as I know, the only applications where active balancing makes economic sense is when you are designing things like a satellite or a rocket or something that needs to be powered by batteries, but where cost is not of primary concern. Every passenger car BMS that I know of that is on the street uses some sort of passive balancing, which is dissipative, but that makes some economic sense for a passenger car type of application.

So the way in which a model like this one here will be useful is if each of these little fellows here, each of the battery cell blocks really behave like a real life battery cell, right? So this battery block that we have in here, if I double-click it, you will see the parameters that characterize it are the parameters associated with that equivalent circuit that we were talking about before. So if I click helping here, you will see an explanation of what each of those parameters is about, right? So that's the equivalent circuit is very similar to the one that we saw before.

We can select the number of RC components, as I said before, from between one and five in this case. And the electrical topology of the equivalent circuit, so how many components, and how they are connected. And its parameters, the parameters that are inside that equivalent circuit, are the ones that are going to give my battery cell the behavior of an NMC cell or an LFP cell or an NCA cell or whatever it may be, right?

So what electrochemically characterizes those types of battery cells are modeled as parameters in an equivalent circuit that depend on SOC on temperature, and on age in a completely general and nonlinear way. So for example, here, we have most of the parameters that we are seeing here are fields of a structure called battery, right? So there's battery. The number next to it means cell number one, cell number two, or cell number three. In this case, it does matter which one we look at because they are all identical.

And this one here E sub m is for electromotive force. So this is going to give me the open circuit voltage or OCV. Every time you see this three letters, you hear LUT. LUT stands for lookup table. Lookup table. So that means that this is going to be a matrix of values that depend on SOC and temperature, as we'll see in a minute.

There's the internal resistance, there's the dynamics. So here we are using a third order equivalence circuit, and in maybe 10 minutes or so we will understand why we used a third order equivalence circuit. So three time constants that are combined to give us the relaxation that we observe experimentally.

There's a place to incorporate degradation. In this case, we're not using that, but we will in two examples from now, the thermal part and so on. So let's take a look at why this is an NMC cell and an LFP cell. So I'm going to hit OK here and show you the parameters in that battery structure.

So that structure has rows and columns. The rows indicate which cell we're talking about. The columns for the fields. So for example, open circuit voltage, or electromotive force. The lookup table, the correct price is that, looks like this. These are volts at open circuit as a function of state of charge and temperature.

So this is-- oops-- this is a I'm going to actually plot this so you can see it more clear. This is the OCV signature of an NMC lithium ion cell. So this is the OCV open circuit voltage from fully charged, 4.3, almost 4.2 volts, down to, in this case, 10% SOC, 3.45 volts or something like that. A significant dependency of the OCV on the state of charge, but not so much on the temperature. So this is the result of a characterization made at three different temperatures, 5, 20, and 40 degrees Celsius.

So you can see here that within that temperature range, The OCV doesn't change all that much, right? The LFP signature would have been pretty different from here. It would have been something like this. The LFP profile would have been something starting from 3.6 going down, and then pretty much constant throughout all the SOC regime, almost up until when it is fully drained that it goes down. And much, much flatter OCV signature than and NMC. So we would have seen something like that.

What does this mean in terms of practical BMS type of workflows? Well, one thing that is clear from this NMC characteristics is that if I want to estimate the state of charge, it is quite possible to calculate the OCV measuring voltage and then making some correction, and then doing a relationship between the OCV and the state of charge.

And this is because there is a significant change in OCV with SOC. Something that doesn't happen with LFP, in LFP what we have is, if we are seeing it from the side, we see, like, an OCV that looks like this. So there's not much change in open circuit voltage with the state of charge, so we really cannot know the SOC measuring voltage, and that's why we need more sophisticated techniques such as the Kalman Filter and things like that.

What happens with the internal resistance? Well, the internal resistance behaves in the opposite way. So there's a much more important dependency on temperature than there is on the state of charge. The internal resistance in most of lithium ion cells typically goes up a little bit at very low and at high SOCs, something like that, a profile like that. But it is exponential with temperature, something that we had said at the very beginning of our conversation.

So now the question becomes, well, I have a battery secular, I have my batteries. How do I gather these numbers? These are my battery fingerprints. These are what would represent the personality of my lithium ion cells. So the question is, well, how do I get this? What kind of experiments do I make in order to come up with these numbers?

And that is the question that I intend to answer with my second example. So remember, what we need now is, given a certain battery cell, well, we need to determine what kind of experiment to perform to figure out those battery cell parameters, those equivalent circuit parameters. So let me actually see if I can show a slide to introduce the subject.

So when we have our battery cell, let's say, at zero current, and at a certain point in time we impose a discharge pulse, and then we remove the current again. Will we see that what we measure from the battery as a result of that is something like this. That the voltage starts at a certain level, it drops because of the internal resistance, and it keeps dropping because again, all the internal resistance and because the open circuit voltage is actually going down because we're discharging it, and when we let go of the current, the voltage recovers.

And it recovers in a very particular way. There is one portion of the voltage that is instantaneous. It recovers just like that, like, suddenly. And then, there is a portion of the voltage recovery that is more or less exponential in shape. And this can take from minutes to hours, depending on the chemistry, depending on the state of charge, and depending on the temperature, and on the H. Four things.

And then, the other thing that happens, of course, is that as the cell is discharged, the open circuit voltage keeps going down, and down, and down until we reach something that's called the cutoff voltage. So the question is, well, what is the simplest equivalent circuit that gives me this response when I excite it in this way?

So this is the very simplest possible equivalent circuit where I have a series resistor that is going to give me the instantaneous voltage drop. If this is the first order exponential relaxation, I only need one of these, where R1 times C1 is the relaxation time for where this portion of the voltage recovery, and the open circuit potential has a certain SOC relationship.

So what we will do is we will use a combination of experiments and simulation in order to perform something called parameter estimation. Parameter estimation is this. It's something that we can do to figure out the parameters of a dynamic system. And the we do this is as follows.

We put together a model of our system. In our case, an equivalent circuit model that the model of a unit cell. And at the same time, we have a characterization experiment that we will see what it looks like in a minute. And I am going to excite my model in exactly the same way as I excited my experiment. And then, the optimization routine in MATLAB is going to compare the output of that excitation, and it is going to adjust to tune, to modify the values of those equivalent circuit parameters until the simulated response matches my experimental response.

So this is what you are going to do with this experiment. The simplest way to do this is using isothermal experiments. Why? Because if we keep the temperature constant, we remove or one of the dependencies from the very beginning. So it is easiest to perform this characterization many times, isothermal, so at the same temperature.

So I control the temperature of the battery cell within the range of temperatures that I care about, and I do the characterization simulation, the characterization procedure at all the temperatures that are meaningful to me. So what kind of experiments can I use? Well, there's no universal answer to that question. This is just one example.

This is what we call a pulsed discharge experiment. And what we are doing is, remember, we keep the temperature constant, we start with the cell fully charged, and we start discharging it by pulses. As we discharge the cell, there is a voltage drop and the recovery of drop, and recovery, and drop, and a recovery.

And immediately you can see that all the relaxations are more or less exponential in shape. So the recoveries are more or less exponentially in shape, but it's also quite apparent that they are different from one another. So that means that if the only thing that is changing in this experiment is the state of charge, which is the only thing that I cannot control independently because it is changing just because I am putting some, like, or extracting some charge out of it, the temperature is the same. So that means that in general, the characteristics of my battery cell are going to be dependent on state of charge.

So that means that the parameters of my equivalent circuit cannot be simple numbers, simple scalars. They have to be to be vectors with elements corresponding to SOC levels in order for the equivalent circuit to have the flexibility for their parameters to be SOC-dependent.

So going back to the picture that I showed a minute ago in PowerPoint, what we need to do, basically, is to figure out how to parameterize the equivalent circuit that is in my Simulink model in order for it to give me this response, which is, by the way, this is real experimental data. So I need my Simulink model to respond like my experiment.

I will need an internal resistance that gives me this recovery. I will need a set of RC components that give me this exponential relaxation. And also, an open circuit voltage that gives me this OCV-dependent downwards trend in OCV.

So let's say I have my experiment. And as I said before, there's no universal experiment that I can tell you about that. You may have heard of something called HPPC, hybrid pulse powered characterization. That's another way of characterizing cells, right?

There are certain things that you need to take into consideration in order to design an experiment. They need to be dynamic enough that they exercise their values of the parameters that you are estimating. And we can talk about this in much more detail, but I don't want to spend too much time in one single example. So let's see what else we need.

The second thing that we need is a model for the cell. And this is something that I already have. My unit cell is here. Now, these values, these parameter values, are not final values. They are just initial guesses, initial conditions that I will use for the optimizer to perform its calculation.

So this is the open circuit potential. This is only one column. Remember there is no temperature change, so there's only one temperature in here, so I don't need the other two columns. What I do need is the SOC dependency, because that's something that is going to change no matter what I do to the cell. So the state of charge is going to evolve as I extract current from it.

So from this 3.8, the optimizer needs to modify these values in order to give me a response that is similar to the one that I measured in the experiment. So what do we do?

Well, we need to inject the pulses, the discharge pulses that are used in the experiment to my simulation and see what happens. So at the beginning, if I do that, I inject these pulses, this is the voltage that I measure, that I simulate as a result. So this is experiment and simulation.

So simulation is clearly wrong because the parameters are not the final parameters. These are my tentative initial guesses. This is the 3.8 that I was telling you about before.

So what we're going to do now, using Simulink's parameter estimation, is we are going to put together an optimization routine that is going to try to minimize the difference between simulation and experiment. So an adjustment of the parameters of my equivalent circuit will bring my simulation closer to my experiment. So let's do that.

And by the way, another thing that I need to decide is, well, what kind of equivalence circuits to use. Let's start with the one-time constant, and then if that is not enough, we'll see what we do. So keep in mind that we are starting the estimation with just one-time constants. And you will see in a very short time that that is not good enough. We will need something else.

So I'm going to now open a tool that works on top of Simulink. That optimization-based adjustment-- let me scale the values here, first-- so that the results that I obtain in this simulation approaches the one that I measured in my experiment. So this tool here that I'm using is called Simulink Design Optimization.

And what it's doing is, it says, well, let's use this Simulink model with the tentative parameters that you gave me at the beginning. So it grabs those parameters and simulates the model. At the beginning, it will simulate the model and it will realize that it is very far away from where it wants to be.

So as long as that is the case, as long as the simulation result is far from my experimental result, what you will do is it will impose a small perturbation to the value of each equivalent circuit element parameter, and it will determine whether that perturbation improved or didn't improve with it. So if it made the situation better, it says, well, this is a good direction. I am going to keep going with the parameter in that direction.

And if it turns out that it didn't improve it, it decides to go in a different direction. So the goal is-- and this is because it is an optimization-based calculation-- the goal is to minimize the difference between my simulated voltage and my experimentally-measured voltage. This takes about eight minutes to complete.

I think what we can do is I can show you. I recorded video of this happening, so that we don't have to wait all the way. Where is it?

So this video is actually doing the same thing that I was showing you in Simulink, but it is doing it with, actually, with three time constants. And it is essential that I use a video, because this takes much more time, it takes more almost 20 minutes, I believe. But what needs to happen as you can probably see, is that the simulation, as the parameter values are adjusted, the simulation looks more and more like the experiment. So when the optimization converges, they are very, very close to one another.

On the estimated parameter window here, what we're seeing is each color representing each equivalent circuit element and each trace or response to each SOC level. So I showed you in an accelerated mode, 23 minutes for all of these parameters. Keep in mind that each of these is actually 10 parameters right, because SOC is part of the gain here, right? So these are three, five, eight, so 80 parameters are, like, being simulated at the same time. So it's a very big optimization problem.

So what I'm going to do with this one, I am not going to wait for this to finish. What I'm going to do is load the final result for the one-time constant situation, and show you why that is actually not good enough. And that is the reason why we ended up using three parameters. Three-- not three parameters, Three RC components.

So this is the best single time constants equivalent circuit could do. Decent fit in here, a little worse in here, and definitely not good enough in here. So what's going on here? Well, it turns out that this battery chemistry, is NMC cell is actually better represented by a third order equivalence circuit. This is a third order relaxation, meaning that it is an exponential curve that is best represented by a superposition of three different time constants of the order of 10, 100, and 1,000 seconds. So that's more or less what you can expect, at least between 10 and 40 degrees Celsius in the NMC cells.

So what do I do when I see this? Well, what I can do is say, you know what? One-time constant is not good enough. Let's change this to three-time constants. So I can modify my battery cell block, I can say, well, one-time constant is not good. Let's use three. And if I use three, I'm going to show you the final results for three-time constants. You will see that the fit is a lot better this way.

So not perfect, especially here. There's a little bit of a problem here, but definitely better than it was before. And the problem is that were using an equivalent circuit that was too simple to explain the third order dynamic response of this cell. Excellent, so let's keep going now.

I am going to go at the more or less same pace this example and the next, and then I am going to start accelerating a little bit. Otherwise, we will not have time to cover all the topics.

So what can we do once we have a good model of the single cell? Well, the first thing that, well, the first type of things that we can do is what we did with the example that I showed at the very beginning. So once this cell is characterized in terms of its voltage, internal resistance, relaxation times, as a function of SOC, temperature, and if I have the data to back this up, age, I can scale that cell up to build a module or a pack, estimate how much heat reduction that battery pack is going to have to be to be dealt with, how much, how big a thermal management system I am going to need, and so on.

Another thing that is a typical use of a battery cell model is state estimation. So state of charge is a very important quantity, very important thing that we need to estimate from a cell. And as I said at the beginning, it is not something that we can measure directly. So we measure some other things. Those things are the temperature, the current, and the voltage.

And using a model of the battery cell, and something like we just determined during the characterization workflow, we can estimate the state of charge, the state of the battery in general, the state of charge in particular. So traditionally, state of charge is estimated by integrating the current that goes in and out.

So if you integrate amps, the results amp hours or amp seconds, which is a measure of the charge. And dividing that by the capacity, you obtained the state of charge. The problem with doing that in that way is that the sensor that you use to measure the current has a certain error, and that error accumulates over time, and then you end up having a much more difficult different real state of charge than the one that your counter is giving you. That's what we call Coulomb counting, and it's the simplest, the cheapest, but not the most accurate way of estimating the SOC.

Estimating SOC using voltage is possible in cases where the discharge profile is not very flat, like I showed at the beginning when I was drawing a picture of the difference between the NMC and the LFP cell. Because in some cases, the voltage doesn't change all that much throughout the range of interest of state of charge, and then that means that I cannot determine state of charge using voltage.

So a method that combines both the Coulomb counting and the voltage measurement, plus a model of the cell, is what we call the Kalman filter, which is a technique that has been used for status estimation in dynamic systems for many decades now. But it turns out that it is very useful for estimating the state of a battery cell.

So what is a Kalman filter? A Kalman filter is a technique that we use to estimate a state where we cannot put a sensor. So for example, if I have a rocket and I want to estimate the temperature in here where maybe the geometry of the system is such that it is not accessible to put a thermocouple there, I could put a thermocouple somewhere else and using the model of this system-- in this case it would be, for example, the way in which heat is transmitted from here to here-- estimate the temperature here, measuring it somewhere else.

How about in batteries? Well, in batteries, what we can measure is the currents and the voltage. So let's say that the current is the input, the voltage is the output, and an internal state is the state of charge, which is the one that we want to determine. So the Kalman filter is an observer that contains a model of the cell. And what it does is the following.

It says, well, if the current is this, then using the model of the cell that I have inside, I am going to estimate what the voltage should be. And that's what the Kalman filter output is. And then, it says, well, in order for this voltage estimation to be the same as the voltage that is actually happening there, I can calculate what the internal states of the battery should be.

So it uses a recursive algorithm that combines the estimation of the voltage output and the measurement of the real voltage in order to do the math and calculate the internal states of the cell. Among them, the state of charge. So let's see how to implement that using Simulink.

On the left, I have my system, my plans, my physical system. This is the same battery cell that we've been dealing with up until now. And the goal here is to estimate the state of charge. So I am going to be doing-- going to push play in here, and then charge and discharge it so you can see that the state of charge will go up and down.

And on this scope, excuse me, what you will see is two traces, one yellow and a blue trace. The yellow is the state of charge as estimated by that Kalman filter, and the blue is the real state of charge, which is something that we never have in reality. This is something that I happen to have here, because this is a simulation of the system. But the goal of this exercise is to initialize the state of charge at a, not the right place.

So here, the initial point is 50% state of charge, but I am actually telling the Kalman filter that the initial state of charge is 60%, in order to see how long it takes for the Kalman filter to actually realize that there is a problem and converge to the real state of charge. So it takes, according to this, this is times 10⁴. So 0.36 is one hour of simulated time, so it takes about an hour of simulated time to converge.

So how is this doing this? Well, current, temperature, and voltage are being measured, as I explained in the previous diagram. And those are being fed to our Kalman filter blocks. So this block here is a block from our control system library that is one of the types of Kalman filters. And what we are doing here is we are giving this block information about our cell in two separate ways.

One is we're indicating the state transition, and the other is we're indicating the measurement. So this is something, we don't have enough time to talk in detail about this, but as I said before, Kalman filter is a recursive algorithm that combines estimation and measurement. So I am just going to show you each of them individually. And if you're interested in this in particular, we can have a follow-up discussion just centered on this.

These are the lookup tables that we have captured during the characterizations. So we are reusing that information, the information that we gathered during our estimation, parameter estimation procedure. And here, what we have is a MATLAB function that represents the equivalent circuit itself. So there are four states, three of them corresponding to the voltage across the RC components. There are three because there are three RC components in this equivalent circuit-- excuse my sloppiness in drawing-- and the state of charge itself.

So this is the discrete equivalent to the equation that defines the state of charge as the integral of the current divided by the capacity. So in here, we're giving the system the information about the dynamic behavior of our equivalent circuit. In the measurement part, what we are saying is, we're giving the Kalman filter the information about the output.

So what is the output? Well, the output is-- if you remember my diagram before-- is the voltage. So if this is the terminal voltage, the terminal voltage in the cell, if we follow the equivalent circuit idea, is equal to the open circuit voltage, which, again, is a lookup table that we obtained during our characterization, minus all the voltage drops across the rest of the components of the equivalence circuit.

The first one is the ohmic drop. I times R0. So the current times the internal resistance. That, again, is one of the lookup tables that we obtained from before. The rest of the voltage drops happened to be the components two, three, and four of the state vector, that, remember, had SOC, V1 V2, and V3.

So in this way, what we are giving the Kalman filter is information about the way in which the state changes and the way in which the Kalman filter is correcting for that estimation using the measurement of the voltage. Because this is a block that shifts with one of our Simulink libraries, it can generate C code automatically. So when you decide to implement this in hardware, you can generate C code from this block directly, and embed that C code in your microcontroller.

So that is one example of how we can do state of charge estimation. In this particular case, we are using one of the nonlinear Kalman filters that we have. UKF stands for unscented Kalman filter. There are three types of nonlinear Kalman filters in our library. The extended Kalman filter, the unscented Kalman filter, and the particle filter. And the reason why we need a nonlinear Kalman filter for battery state estimation is that the relationship between the OCV and the state of charge is nonlinear, so we cannot use a traditional Kalman filter.

What about this one, here? So same idea s before, but now to our traditional cell that is identical to the one that we saw before, we are adding one more thing, which is the increase in internal resistance. In this case, I am doing this in a very, very exaggerated way. So I am making this degrade exceedingly fast in order to have a simulation that runs in a reasonable amount of time, because I typically use this in the context of conversations like the one that we are having now.

So what I am doing here, is I am making the internal resistance of the unit cell grow with number of cycles. So if we take a look at the Help section here, with this battery cell where we are implementing aging, what we are doing is we are making the resistance grow with the square root of the number of cycles. So this is what we are going to do with the Kalman filter to make this modification.

This system looks very similar to the one before. I'm using an extended Kalman filter as opposed to an unscented Kalman filter. But here, the number of states is actually not four but five. And the fifth is actually the internal resistance.

So take a look at this have this trick that I implemented here. And this is, by the way, all of the examples that I am sharing with you are going to be available for you to download from a place that we will indicate. So you will be able to try all of these examples on your own, on your own time. But anyway, so what am I doing here?

So here's the trick. This is identical to everything that we had before, but this one is saying, as far as I am concerned, the change in internal resistance is zero. So that the internal resistance doesn't have, as far as the state equation is concerned, doesn't have any reason to change. But because in addition to state estimation, I am doing measurements, here's what I'm doing.

Again, same idea as before. Terminal voltage is equal to open circuit voltage minus, and look at this, the ohmic drop is now I, the current, times R0, but R0 is no longer a constant of the lookup table, R0 is now components number 5 of our state vector. So combining the state equation and this modified measurement, I am making the Kalman filter believe that R0 is a state, like a state within quotes.

It's a parameter, but I am making a change. So what the Kalman filter is doing, is it is, every time it sees a change in current, it observes what the changing voltage is as a result of that. And because it is seeing it increase over time, it interprets that as an increase in internal resistance. So you will see that the internal resistance, as estimated by the Kalman filter here, is going to be growing more or less as the square root of the time, which because we are doing this using a repetitive cycle, is more or less the same as number of cycles.

So this is current. And I am repeating a current pattern. And as you can see in the voltage, the voltage drop is actually increasing in amplitude over time. And that is the result of the resistance going up. So the Kalman filter is realizing that this is happening. So the voltage is overall changing-- I didn't mean to do that. I meant to do something like a wedge. This amplitude is smaller than this amplitude. That's all I want to say. So a modification of the Kalman filter idea to capture a change in internal resistance, in addition to the change in state of charge, which we already had from before, and there's no change in that, in that sense.

So let's now switch gears and talk about the BMS, the algorithm part of all this story. OK. So up until now, we've been talking about this side of the business, the plants, mostly. Well, the last example was about an algorithm. But it was not about everything that a BMS needs to do.

So here there is a six-cell battery cell module. And on this side, on the left-hand side, there is the algorithmic part of the quantity. So let's take a look at this. We're going to be using a combination of Simulink and a tool that you may have heard of that's called state flow for state estimation. So we're doing four main things in this example.

First of all, you may have heard of a SOP or state of power. What that entails is to calculate what kind of currents I am going to allow my battery pack to give me in order to-- as I said at the beginning-- in order to keep the battery pack within the voltage, current, and SOC, and temperature ranges that I am required to.

So let's start with the current. That needed to not exceed the-- oops, sorry about that. We need to keep the voltage of the cell within two limits, the lower voltage limits and the upper voltage limit. They are called the voltage cut off limits.

So given a certain voltage limit, what we can do is we can compare the voltage that we are at with that voltage limit, divide that difference by a certain measure of the internal resistance of the cell, and that is going to give us the maximum current that we can allow the system to have. So that is going to give us one of the current thresholds.

The other two are going to be given by a thermal consideration. So as I said at the beginning, there are current levels that need to be respected depending on how warm or how cold our battery cells are. And those are specified by the manufacturer.

So for example, I cannot charge my battery cell at temperatures below zero Celsius. So that's a temperature limit that I cannot exceed. So I can calculate that with a lookup table in here and put it in there.

I also want to limit the amount of current that is flowing out of the cell when the temperature is very high, because that is going to cost an excessively high temperature because of the dual effect, and that is something that I also want to avoid. So once I have independently calculated the three temperature limits, I can select the minimum of the three of them and that is going to be my discharge current limit.

And I can do the same thing for charge. So the calculation is the same. The parameters are going to be different because in general, the charging procedure is more delicate than the discharging procedure.

The second thing that we're seeing here is the state of the battery pack. So forgive me, this is a very busy diagram, but there's several state machines that are determining if the battery pack is being standby, driving, charging, or in fault condition. If anything goes wrong, as being determined by this fault monitoring diagram here, we will immediately open the contactors and stop any operation with a battery pack.

This is the tool that I was telling you about, state flow. It is very useful for the design of state machines. What you see inside the states are the functions that are executed while the state is active, and the conditions that you see on top of the transitions are the conditions that need to be satisfied for that transition to occur. So there are some requirements that need to be followed in order, for example, to go from standby to charging, or from charging to driving, and so on.

The two states at the bottom are the ones that manage the contactors. So the opening and closing charging and inverter contactors require us to follow a certain sequence because there is some pre-charged contactors, for example, that need to be utilized before we start charging in order to avoid an excessively high current in rush, in the case that the voltage of the battery pack is very different from the voltage that is charging it. So that's how we manage that.

The third procedure, we already saw an example of that, is the state of charge. I'm not going to dwell on this in any level of detail, we already saw that. We are implementing three different methods in the same place. This is not required. You typically choose one of them. But we wanted to show the difference between using Coulomb counting and the three Kalman filter methods in one example for our customers to evaluate the different characteristics among them.

And the last one is the balancing algorithm. And this is very similar to the algorithm that we saw during the first example of the morning, although in this case, this is a more refined version of it because it uses MATLAB's vectorization functions in order for the algorithm to be valid no matter the size of the module. So this same algorithm can be utilized with any number of cells in series. So it's a more general algorithm than the one that we saw at the beginning.

It uses a little bit of a temporal logic in here in order to avoid chattering. Dual thresholds, it controls the procedure that is called hysteresis control. So unfortunately, we don't have a lot of time to go in detail into it, but as I said before, we can always come back to this on a one-on-one basis, and you will have the sample to look at on your own time, if you so wish.

So once we have our algorithm part evaluated, we can connect it to our model of a plant and run different scenarios with our model. How about a very hot day in the south, in Shenzhen, for example. What happens if I charge and immediately start driving? Things like that. Will that trigger any issue with our battery pack? So that's the type of analysis that we can perform using a model of this kind.

And we've architected this example so that it is ready for co-generation, so you can very easily you do hardware the loop with this. And there are a couple of videos on MathWorks.com that show how to implement this in a hill bench. So if you're interested in that piece, by all means, feel free to browse to that site, if testing and simulation is part of what you do.

All right, we have a few minutes left, so I want to use them to talk a little bit about the deep learning part of our presentation. So this is the last example that I have for you. And it's the last one I've been working with.

And it is not related to simulating a battery pack. What it is doing, it's a result of the part of a PhD thesis of a friend of mine who's studying at McMaster University, and they have kindly let us use this example. The data is publicly available, so you can also download it from the website that, it's written here.

And what is the motivation for using these statistical techniques in battery technology? Well, there's a few of them. Remember, close to the beginning of our conversation we said that it is difficult to figure out the interaction between the operating conditions that cause battery cell degradation. Well, one of the possible answers to that problem is to say, well, instead of trying to understand from the physical point of view each of the conditions that cause battery degradation, let's instead measure from the field from cars being driven on the streets.

Let's measure the variables that are changing in the battery, and using a statistical method, such as a neural network, let's train the neural network in order for the neural network to learn the patterns that cause a certain change of state that we are interested in determining. For example, the state of charge, as is the case of this example, or even the state of health, if I have access to the battery once in a while to make an evaluation of the real SOH.

And once that procedure is trained, once it has been fed with enough data, then it will be able, hopefully, to predict the state of charge in subsequent times. It will learn a pattern, and when it sees a certain pattern, it will be able to indicate that that type of degradation that is going on in there.

So this example is about subjecting the cell to a certain combination of conditions. So different voltages, different temperatures, different C-rates, and it is trained to learn the way in which the SOC is changing. So at the same time this is happening, there is a very accurate measurement of the state of charge and the neural network is learning, what is the relationship between the change in these measurable parameters and the state of charge that is not measurable directly, like we said before?

So this is part of our deep learning toolbox. There are several types of neural networks that we can choose from. And forgive me, I'm not an expert in deep learning or for anything like that, so I don't really know exactly the mathematical meaning of all of these parameters that they used to tune the neural network. They are repeating the training five times, and they are training with a certain number of iterations.

Originally, it was 5,100. I repeated that procedure with 1,000. And these were the results. This is the architecture of layers. These are the options. And here, finally, is where we create a network object by training it with the input data and the options.

So the procedure goes on. This takes, with a GPU, about 20 minutes to happen, for the 1,000 iterations, so that you know. I couldn't do this with my computer because I don't have a GPU. I leased a computer from our headquarters in Boston. It is very useful to have a GPU in this case, because it is a very intense computation.

But what I wanted to show you is results of this, typically the way in which the error goes down, this is the root mean square error for the five runs at different temperatures. So it's typically the case that at lower temperatures we have higher level of error. And at the very end of the script, we have the difference, or for a comparison, between the observed SOC and the predicted SOC.

And you can see that the neural network does a pretty good job learning the pattern of change instead of charge. And it gets even better at a warmer and warmer temperatures. So what is the idea with this? Well, the idea is the following. if you have a cell in the lab, you cycle it while you are training a neural network. Once it gives you enough accuracy, you generate C code from that net object that I showed at the beginning, and then you deploy that as C code in your microcontroller.

So if the training data was rich enough to be representative of any possible situation, then there's going to be enough information in that object, so that in the future, that your network can learn from the current voltage and temperature measurements, and with the internal algorithm, predict the state of charge. And we didn't need any Kalman filter or any Coulomb counter, or anything like that.

So I bring this to the table as something that the battery engineering community is starting to look at very seriously. My personal goal as a follow-up from this is going to extend these to SOH estimation, for which I need to partner up with the university again, so that instead of detecting changes in state of charge, we detect capacity fate and resistance built up.

So with that, we are at the end of our morning, now. Let me summarize what we saw so far. We started talking about characterization using experiments and optimization-based parameter estimation routine. We saw an example of small battery pack with its thermal effects.

We talked about state of charge and set of health estimation using Kalman filters. We briefly brushed over BMS algorithm development. And the last five or 10 minutes, we talked about something different, which is the use of deep learning for state estimation.