visualize
Visualize and validate filter response
Description
visualize( plots the
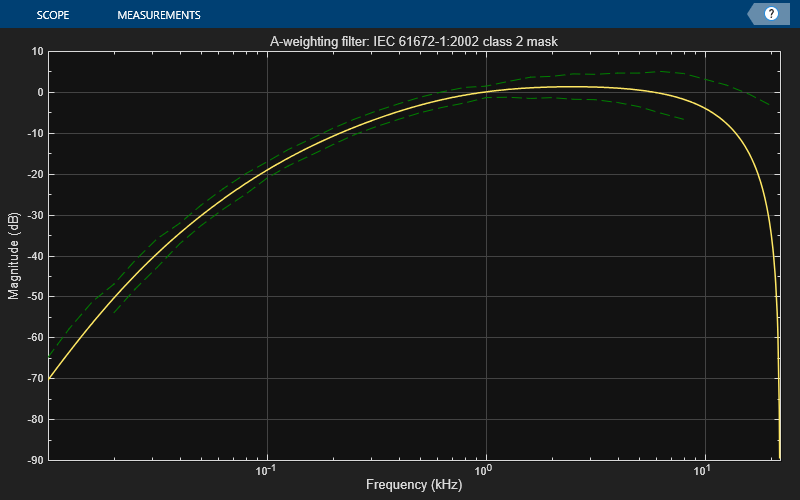
magnitude response of the frequency-weighted filter weightFilt)weightFilt.
The plot is updated automatically when properties of the object change.
visualize(
uses an weightFilt,N)N-point FFT to calculate the magnitude response.
visualize(___, creates
a mask based on the class of filter specified by mType)mType, using
either of the previous syntaxes.
hvsz = visualize(___)dsp.DynamicFilterVisualizer object when called with any of the
previous syntaxes.
Examples
Input Arguments
Version History
Introduced in R2016b