comm.SymbolSynchronizer
Correct symbol timing clock skew
Description
The comm.SymbolSynchronizer
System object™ corrects symbol timing clock skew between a
single-carrier transmitter and receiver for PAM, PSK, QAM, and OQPSK modulation schemes. For
more information, see Symbol Synchronization Overview.
Note
The input signal operates on a sample-rate basis and the output signal operates on a symbol-rate basis.
To correct symbol timing clock skew:
Create the
comm.SymbolSynchronizerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
symbolSync = comm.SymbolSynchronizer
symbolSync = comm.SymbolSynchronizer(Name,Value)comm.SymbolSynchronizer('Modulation','OQPSK') configures the symbol
synchronizer System object for an OQPSK-modulated input signal. Enclose each property name in
quotes.
Tunable DampingFactor,
NormalizedLoopBandwidth, and DetectorGain
properties enable you to optimize synchronizer performance in your simulation loop without
releasing the object.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Modulation type, specified as 'PAM/PSK/QAM' or
'OQPSK'. When using OQPSK modulation, see Tips.
Tunable: No
Data Types: char | string
Timing error detector method, specified as Zero-Crossing
(decision-directed), Gardner (non-data-aided),
Early-Late (non-data-aided), or Mueller-Muller
(decision-directed). This property assigns the timing error detection scheme
used in the synchronizer. For more information, see Timing Error Detection (TED).
Tunable: No
Data Types: char | string
Samples per symbol, specified as an integer greater than 1. For more information, see Nsps in Loop Filter.
Tunable: No
Data Types: double
Damping factor of the loop filter, specified as a positive scalar. For more information, see ζ in Loop Filter.
Tunable: Yes
Data Types: double | single
Normalized bandwidth of the loop filter, specified as a scalar in the range (0, 1). The loop bandwidth (Bn) is normalized to the symbol rate (Ts) of the input signal. For more information, see BnTs in Loop Filter.
Note
To ensure the symbol synchronizer locks, set the
NormalizedLoopBandwidth property to a value less than
0.1.
Tunable: Yes
Data Types: double | single
Phase detector gain, specified as a positive scalar. For more information, see Kp in Loop Filter.
Tunable: Yes
Data Types: double | single
Usage
For versions earlier than R2016b, use the step
function to run the System object algorithm. The arguments to step are the
object you created, followed by the arguments shown in this section.
For example, y = step(obj,x) and y = obj(x) perform equivalent operations.
Description
symbols = symbolSync(samples)
The input operates on a sample-rate basis and the output signal operates on a symbol-rate basis.
You can tune the
DampingFactor,NormalizedLoopBandwidth, andDetectorGainproperties to improve the synchronizer performance.
Input Arguments
Input samples, specified as a scalar or column vector of a PAM-, PSK-, QAM-, or OQPSK-modulated single-carrier signal.
Data Types: double | single
Complex Number Support: Yes
Output Arguments
Synchronized symbols, returned as a variable-sized column vector. The output
symbols inherit the data type from the input samples. For an input with dimensions
Nsamp-by-1, this output has dimensions
Nsym-by-1.
Nsym is approximately equal to
Nsamp divided by
Nsps, where
Nsps is equal to the SamplesPerSymbol
property value. The output length is truncated if it exceeds the maximum output size
of .
Estimated timing error for each input sample, returned as a scalar in the range
[0, 1] or column vector of elements in the range [0, 1]. The estimated timing error is
normalized to the input sample rate. timingErr has the same data
type and size as input samples.
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Correct a fixed symbol timing error on a noisy QPSK-modulated signal. Check the bit error rate (BER) of the synchronized received signal.
Initialize simulation parameters.
M = 4; % Modulation order for QPSK nSym = 5000; % Number of symbols in a packet sps = 4; % Samples per symbol timingErr = 2; % Samples of timing error snr = 15; % Signal-to-noise ratio (dB)
Create root raised cosine (RRC) transmit and receive filter System objects.
txfilter = comm.RaisedCosineTransmitFilter( ... OutputSamplesPerSymbol=sps); rxfilter = comm.RaisedCosineReceiveFilter( ... InputSamplesPerSymbol=sps, ... DecimationFactor=sps/2);
Create a symbol synchronizer System object to correct the timing error.
symbolSync = comm.SymbolSynchronizer;
Generate random M-ary symbols and apply QPSK modulation.
data = randi([0 M-1],nSym,1); modSig = pskmod(data,M,pi/4);
Create a delay object to introduce a fixed timing error of 2 samples. Because the transmit RRC filter outputs 4 samples per symbol, 1 sample is equivalent to a 1/4 symbol through the fixed delay and channel. Round the fixed delay to the nearest integer symbol.
fixedDelay = dsp.Delay(timingErr); fixedDelaySym = ceil(fixedDelay.Length/sps);
Filter the modulated signal through a transmit RRC filter by using the txfilter object. Apply a signal timing error by using the fixedDelay object.
txSig = txfilter(modSig); delaySig = fixedDelay(txSig);
Pass the delayed signal through an AWGN channel with a 15 dB signal-to-noise ratio.
rxSig = awgn(delaySig,snr,'measured');Filter the modulated signal through a receive RRC filter by using the rxfilter object. Display the scatter plot. Due to the timing error, the received signal does not align with the expected QPSK reference constellation.
rxSample = rxfilter(rxSig); scatterplot(rxSample(1001:end),2)
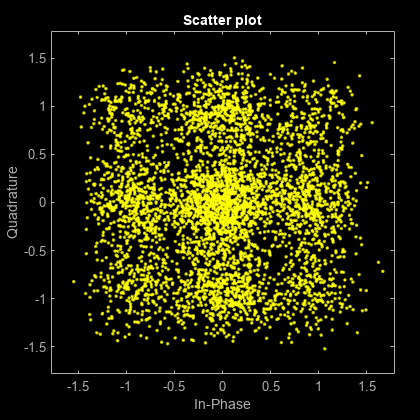
Correct the symbol timing error by using the symbolSync object. Display the scatter plot. The synchronized signal now aligns with the expected QPSK constellation.
rxSync = symbolSync(rxSample); scatterplot(rxSync(1001:end),2)

Demodulate the QPSK signal.
recData = pskdemod(rxSync,M,pi/4);
Compute, in symbols, the total system delay due to the fixed delay and the transmit and receive RRC filters.
sysDelay = dsp.Delay(fixedDelaySym + ... txfilter.FilterSpanInSymbols/2 + ... rxfilter.FilterSpanInSymbols/2);
Compute the BER, taking into account the system delay.
[numErr,ber] = biterr(sysDelay(data),recData)
numErr = 11
ber = 0.0011
Correct a fixed symbol timing error on a noisy BPSK transmission signal. Check the bit error rate (BER) of the synchronized received signal.
Initialize simulation parameters.
M = 2; % Modulation order for BPSK nSym = 20000; % Number of symbols in a packet sps = 4; % Samples per symbol timingErr = 2; % Samples of timing error snr = 15; % Signal-to-noise ratio (dB)
Create root raised cosine (RRC) transmit and receive filter System objects.
txfilter = comm.RaisedCosineTransmitFilter( ... OutputSamplesPerSymbol=sps); rxfilter = comm.RaisedCosineReceiveFilter( ... InputSamplesPerSymbol=sps,DecimationFactor=1);
Create a symbol synchronizer System object™ to correct the timing error.
symbolSync = comm.SymbolSynchronizer( ... SamplesPerSymbol=sps, ... NormalizedLoopBandwidth=0.01, ... DampingFactor=1.0, ... TimingErrorDetector='Early-Late (non-data-aided)');
Generate random data symbols and apply BPSK modulation.
data = randi([0 M-1],nSym,1); modSig = pskmod(data,M);
Create a delay object to introduce a fixed timing error of 2 samples. Because the transmit RRC filter outputs 4 samples per symbol, 1 sample is equivalent to a 1/4 symbol through the fixed delay and channel. Round the fixed delay to the nearest integer symbol.
fixedDelay = dsp.Delay(timingErr); fixedDelaySym = ceil(fixedDelay.Length/sps);
Filter the modulated signal through a transmit RRC filter by using the txfilter object. Apply a signal timing error by using the fixedDelay object.
txSig = txfilter(modSig); delayedSig = fixedDelay(txSig);
Pass the delayed signal through an AWGN channel.
rxSig = awgn(delayedSig,snr,'measured');Filter the modulated signal through a receive RRC filter by using the rxfilter object. Display the scatter plot. Due to the timing error, the received signal does not align with the expected BPSK reference constellation.
rxSample = rxfilter(rxSig); scatterplot(rxSample(10000:end),2)

Correct the symbol timing error by using the symbolSync object. Display the scatter plot. The synchronized signal now aligns with the expected BPSK constellation.
rxSync = symbolSync(rxSample); scatterplot(rxSync(10000:end),2)

Demodulate the BPSK signal.
recData = pskdemod(rxSync,M);
Compute, in symbols, the total system delay due to the fixed delay and the transmit and receive RRC filters.
sysDelay = dsp.Delay(fixedDelaySym + ... txfilter.FilterSpanInSymbols/2 + ... rxfilter.FilterSpanInSymbols/2);
Account for changes in output data length due to symbol synchronizer resampling and compute the BER, taking into account the system delay.
outLength = min(length(data),length(recData));
[numErr1,ber1] = biterr( ...
sysDelay(data(1:outLength)),recData(1:outLength))numErr1 = 6
ber1 = 3.0000e-04
Correct symbol timing and frequency offset errors by using the comm.SymbolSynchronizer and comm.CarrierSynchronizer System objects.
Configuration
Initialize simulation parameters.
M = 16; % Modulation order nSym = 2000; % Number of symbols in a packet sps = 2; % Samples per symbol spsFilt = 8; % Samples per symbol for filters and channel spsSync = 2; % Samples per symbol for synchronizers lenFilt = 10; % RRC filter length
Create a matched pair of root raised cosine (RRC) filter System objects for transmitter and receiver.
txfilter = comm.RaisedCosineTransmitFilter( ... FilterSpanInSymbols=lenFilt, ... OutputSamplesPerSymbol=spsFilt, ... Gain=sqrt(spsFilt)); rxfilter = comm.RaisedCosineReceiveFilter( ... FilterSpanInSymbols=lenFilt, ... InputSamplesPerSymbol=spsFilt, ... DecimationFactor=spsFilt/2, ... Gain=sqrt(1/spsFilt));
Create a phase-frequency offset System object to introduce a 100 Hz Doppler shift.
doppler = comm.PhaseFrequencyOffset( ... FrequencyOffset=100, ... PhaseOffset=45, ... SampleRate=1e6);
Create a variable delay System object to introduce timing offsets.
varDelay = dsp.VariableFractionalDelay;
Create carrier and symbol synchronizer System objects to correct for Doppler shift and timing offset, respectively.
carrierSync = comm.CarrierSynchronizer( ... SamplesPerSymbol=spsSync); symbolSync = comm.SymbolSynchronizer( ... TimingErrorDetector='Early-Late (non-data-aided)', ... SamplesPerSymbol=spsSync);
Create constellation diagram System objects to view the results.
refConst = qammod(0:M-1,M,UnitAveragePower=true); cdReceive = comm.ConstellationDiagram( ... ReferenceConstellation=refConst, ... SamplesPerSymbol=spsFilt,Title='Received Signal'); cdDoppler = comm.ConstellationDiagram( ... ReferenceConstellation=refConst, ... SamplesPerSymbol=spsSync, ... Title='Frequency Corrected Signal'); cdTiming = comm.ConstellationDiagram( ... ReferenceConstellation=refConst, ... SamplesPerSymbol=spsSync, ... Title='Frequency and Timing Synchronized Signal');
Main Processing Loop
The main processing loop:
Generates random symbols and applies QAM modulation.
Filters the modulated signal.
Applies frequency and timing offsets.
Passes the transmitted signal through an AWGN channel.
Filters the received signal.
Corrects the Doppler shift.
Corrects the timing offset.
for k = 1:15 data = randi([0 M-1],nSym,1); modSig = qammod(data,M,UnitAveragePower=true); txSig = txfilter(modSig); txDoppler = doppler(txSig); txDelay = varDelay(txDoppler,k/15); rxSig = awgn(txDelay,25); rxFiltSig = rxfilter(rxSig); rxCorr = carrierSync(rxFiltSig); rxData = symbolSync(rxCorr); end
Visualization
Plot the constellation diagrams of the received signal, frequency corrected signal, and frequency and timing synchronized signal. Specific constellation points cannot be identified in the received signal and can be only partially identified in the frequency corrected signal. However, the timing and frequency synchronized signal aligns with the expected QAM constellation points.
cdReceive(rxSig)

cdDoppler(rxCorr)

cdTiming(rxData)

Correct a monotonically increasing symbol timing error on a noisy 8-PSK signal. Display the normalized timing error.
Initialize simulation parameters.
M = 8; % Modulation order nSym = 5000; % Number of symbol in a packet sps = 2; % Samples per symbol nSamp = sps*nSym; % Number of samples in a packet
Create root raised cosine (RRC) transmit and receive filter System objects.
txfilter = comm.RaisedCosineTransmitFilter( ... 'OutputSamplesPerSymbol',sps); rxfilter = comm.RaisedCosineReceiveFilter( ... 'InputSamplesPerSymbol',sps, ... 'DecimationFactor',1);
Create a variable fractional delay System object™ to introduce a monotonically increasing timing error.
varDelay = dsp.VariableFractionalDelay;
Create a symbol synchronizer System object to correct the timing error.
symbolSync = comm.SymbolSynchronizer(... 'TimingErrorDetector','Mueller-Muller (decision-directed)', ... 'SamplesPerSymbol',sps);
Generate random 8-ary symbols and apply 8-PSK modulation.
data = randi([0 M-1],nSym,1); modSig = pskmod(data,M,pi/8);
Filter the modulated signal through a raised cosine transmit filter and apply a monotonically increasing timing delay.
vdelay = (0:1/nSamp:1-1/nSamp)'; txSig = txfilter(modSig); delaySig = varDelay(txSig,vdelay);
Pass the delayed signal through an AWGN channel with a 15 dB signal-to-noise ratio.
rxSig = awgn(delaySig,15,'measured');Filter the modulated signal through a receive RRC filter. Display the scatter plot. Due to the timing error, the received signal does not align with the expected 8-PSK reference constellation.
rxSample = rxfilter(rxSig); scatterplot(rxSample,sps)

Correct the symbol timing error by using the symbolSync object. Display the scatter plot. The synchronized signal now aligns with the expected 8-PSK constellation.
[rxSym,tError] = symbolSync(rxSample); scatterplot(rxSym(1001:end))

Plot the timing error estimate. Over time, the normalized timing error increases to 1 sample.
figure plot(vdelay,tError) xlabel('Time (s)') ylabel('Timing Error (samples)')

Tips
Demodulate symbol-timing synchronized, OQPSK-modulated signals by using the
pskdemodfunction. You can not OQPSK demodulate the output of thecomm.SymbolSynchronizerSystem object because, for an OQPSK-modulated input signal, the object outputs a symbol-rate QPSK-modulated signal. Thecomm.OQPSKDemodulatorSystem object requires an OQPSK-modulated input signal with two samples per symbol.
Algorithms
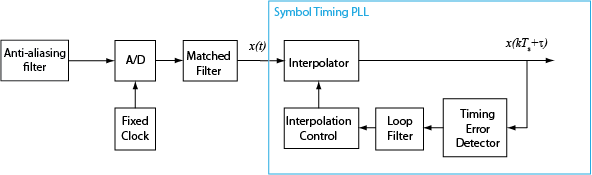
The symbol timing synchronizer algorithm is based on a phased lock loop (PLL) algorithm that consists of four components:
Timing error detector (TED)
Interpolator
Interpolation controller
Loop filter
For OQPSK modulation, the in-phase and quadrature signal components are first aligned (as in QPSK modulation) using a state buffer to cache the last half symbol of the previous input. After initial alignment, the remaining synchronization process is the same as for QPSK modulation.
This block diagram shows an example of a timing synchronizer. In the figure, the symbol timing PLL operates on x(t), the received sample signal after matched filtering. The symbol timing PLL outputs the symbol signal, , after correcting for the clock skew between the transmitter and receiver.
The symbol timing synchronizer supports non-data-aided TED and decision-directed TED methods. This table shows the timing estimate expressions for the TED method options.
| TED Method | Expression |
|---|---|
Zero-crossing (decision-directed) | |
Gardner (non-data-aided) | |
Early-late (non-data-aided) | |
Mueller-Muller (decision-directed) |
The non-data-aided TED (Gardner and early-late) methods use received samples without any knowledge of the transmitted signal or the results of the channel estimation. Non-data-aided TED is used to estimate the timing error for signals with modulation schemes that have constellation points aligned with the in-phase or quadrature axis. Examples of signals suitable for the Gardner or early-late methods include QPSK-modulated signals with a zero phase offset that has points at {1+0i, 0+1i, -1+0i, 0−1i} and BPSK-modulated signals with a zero phase offset.
The early-late method is similar to the Gardner method but the Gardner method performs better in systems with high SNR values because it has lower self noise than the early-late method.
Gardner method — The Gardner method is a non-data-aided feedback method that is independent of carrier phase recovery. It is used for baseband systems and modulated carrier systems. More specifically, this method is used for systems that use a linear modulation type with Nyquist pulses that have an excess bandwidth between approximately 40% and 100%. Examples include systems that use PAM, PSK, QAM, or OQPSK modulation and that shape the signal using raised cosine filters whose rolloff factor is between 0.4 and 1. In the presence of noise, the performance of this timing recovery method improves as the excess bandwidth increases (or rolloff factor increases in the case of a raised cosine filter). The Gardner method is similar to the early-late gate method.
Early-late method — The early-late method is a non-data-aided feedback method. It is used for systems that use a linear modulation type such as PAM, PSK, QAM, or OQPSK modulation. For example, systems using a raised cosine filter with Nyquist pulses. In the presence of noise, the performance of this timing recovery method improves as the excess bandwidth of the pulse increases (or rolloff factor increases in the case of a raised cosine filter).
The decision-directed TED (zero-crossing and Mueller-Muller) methods use the sign function to estimate the
in-phase and quadrature components of received samples, which results in lower
computational complexity than the non-data-aided TED methods.
Zero-crossing method — The zero-crossing method is a decision-directed technique that requires 2 samples per symbol at the input to the synchronizer. It is used in low-SNR conditions for all values of excess bandwidth and in moderate-SNR conditions for moderate excess bandwidth factors in the approximate range [0.4, 0.6].
Mueller-Muller method — The Mueller-Muller method is a decision-directed feedback method that requires prior recovery of the carrier phase. When the input signal has Nyquist pulses (for example, when using a raised cosine filter), the Mueller-Muller method has no self noise. For narrowband signaling in the presence of noise, the performance of the Mueller-Muller method improves as the excess bandwidth factor of the pulse decreases.
Because the decision-directed methods (zero-crossing and Mueller-Muller) estimate
timing error based on the sign of the in-phase and quadrature components of signals
passed to the synchronizer, they are not recommended for constellations that have
points with either a zero in-phase or a quadrature component. and are the in-phase and quadrature components of the input signals to
the timing error detector, where is the estimated timing error. The Mueller-Muller method
coefficients and are the estimates of and . The timing estimates are made by applying the sign function to the in-phase
and quadrature components and are used for only the decision-directed TED
methods.
The time delay is estimated from the fixed-rate samples of the matched filter, which are asynchronous with the symbol rate. Because the resulting samples are not aligned with the symbol boundaries, an interpolator is used to "move" the samples. Because the time delay is unknown, the interpolator must be adaptive. Moreover, because the interpolant is a linear combination of the available samples, it can be thought of as the output of a filter.

The interpolator uses a piecewise parabolic interpolator with a Farrow structure and coefficient α set to 1/2 (see Rice, Michael, Digital Communications: A Discrete-Time Approach).
Interpolation control provides the interpolator with the basepoint index and fractional interval. The basepoint index is the sample index nearest to the interpolant. The fractional interval is the ratio of the time between the interpolant and its basepoint index and the interpolation interval.

Interpolation is performed for every sample, and a strobe signal is used to determine if the interpolant is output. The synchronizer uses a modulo-1 counter interpolation control to provide the strobe and the fractional interval for use with the interpolator.
The synchronizer uses a proportional-plus integrator (PI) loop filter. The proportional gain, K1, and the integrator gain, K2, are calculated by
and
The interim term, θ, is given by
where:
Nsps is the number of samples per symbol.
ζ is the damping factor.
BnTs is the loop bandwidth (Bn) normalized to the symbol rate (Ts).
Kp is the detector gain.

References
[1] Rice, Michael. Digital Communications: A Discrete-Time Approach. Upper Saddle River, NJ: Prentice Hall, 2008.
[2] Mengali, Umberto and Aldo N. D’Andrea. Synchronization Techniques for Digital Receivers. New York: Plenum Press, 1997.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2015a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)