getComponents
Extract SISO control components from a 2-DOF PID controller
Description
[
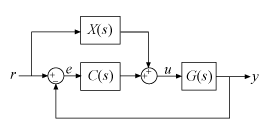
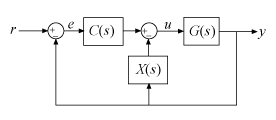
decomposes the 2-DOF PID controller C,X] =
getComponents(C2,looptype)C2 into two SISO control
components. One of the control components, C, is a 1-DOF PID
controller. The other, X, is a SISO dynamic system. When
C and X are connected in the loop
structure specified by looptype, the resulting closed-loop
system is equivalent to the 2-DOF control loop.
For more information about 2-DOF PID control architectures, see Two-Degree-of-Freedom PID Controllers.
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2015b