Cluster Data with a Self-Organizing Map

Clustering data is another excellent application for neural networks. This process involves grouping data by similarity. For example, you might perform:

• Market segmentation by grouping people according to their buying patterns

• Data mining by partitioning data into related subsets

• Bioinformatic analysis by grouping genes with related expression patterns

Suppose that you want to cluster flower types according to petal length, petal width, sepal length, and sepal width. You have 150 example cases for which you have these four measurements.

As with function fitting and pattern recognition, there are two ways to solve this problem:

• Use the Neural Net Clustering app, as described in Cluster Data Using the Neural Net Clustering App.

• Use command-line functions, as described in Cluster Data Using Command-Line Functions.

It is generally best to start with the app, and then use the app to automatically generate command-line scripts. Before using either method, first define the problem by selecting a data set. Each of the neural network apps has access to sample data sets that you can use to experiment with the toolbox (see Sample Data Sets for Shallow Neural Networks). If you have a specific problem that you want to solve, you can load your own data into the workspace. The next section describes the data format.

Defining a Problem

To define a clustering problem, arrange input vectors (predictors) to be clustered as columns in an input matrix. For instance, you might want to cluster this set of 10 two-element vectors:

predictors = [7 0 6 2 6 5 6 1 0 1; 6 2 5 0 7 5 5 1 2 2]

The next section shows how to train a network to cluster data, using the Neural Net Clustering app. This example uses an example data set provided with the toolbox.

Cluster Data Using the Neural Net Clustering App

This example shows how to train a shallow neural network to cluster data using the Neural Net Clustering app.

Open the Neural Net Clustering app using nctool.

nctool

Select Data

The Neural Net Clustering app has example data to help you get started training a neural network.

To import the example iris flower clustering data, select Import > Import Iris Flowers Data Set. If you import your own data from file or the workspace, you must specify the predictors and whether the observations are in rows or columns.

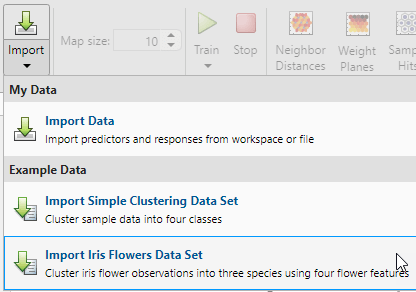
Information about the imported data appears in the Model Summary. This data set contains 150 observations, each with four features.

Create Network

For clustering problems, the self-organizing feature map (SOM) is the most commonly used network. This network has one layer, with neurons organized in a grid. Self-organizing maps learn to cluster data based on similarity. For more information on the SOM, see Cluster with Self-Organizing Map Neural Network.

To create the network, specify the map size, this corresponds to the number of rows and columns in the grid. For this example, set the Map size value to 10, this corresponds to a grid with 10 rows and 10 columns. The total number of neurons is equal to the number of points in the grid, in this example, the map has 100 neurons. You can see the network architecture in the Network pane.

Train Network

To train the network, click Train. In the Training pane, you can see the training progress. Training continues until one of the stopping criteria is met. In this example, training continues until the maximum number of epochs is reached.

Analyze Results

To analyze the training results, generate plots. For SOM training, the weight vector associated with each neuron moves to become the center of a cluster of input vectors. In addition, neurons that are adjacent to each other in the topology should also move close to each other in the input space, therefore it is possible to visualize a high-dimensional inputs space in the two dimensions of the network topology. The default topology of the SOM is hexagonal.

To plot the SOM Sample Hits, in the Plots section, click Sample Hits. This figure shows the neuron locations in the topology, and indicates how many of the observations are associated with each of the neurons (cluster centers). The topology is a 10-by-10 grid, so there are 100 neurons. The maximum number of hits associated with any neuron is 5. Thus, there are 5 input vectors in that cluster.

Plot the weight planes (also referred to as component planes). In the Plots section, click Weight Planes. This figure shows a weight plane for each element of the input features (four, in this example). The plot shows the weights that connect each input to each of the neurons, with darker colors representing larger weights. If the connection patterns of two features are very similar, you can assume that the features are highly correlated.

If you are unhappy with the network performance, you can do one of the following:

• Train the network again. Each training will have different initial weights and biases of the network, and can produce an improved network after retraining.

• Increase the number of neurons by increasing the map size.

• Use a larger training data set.

You can also evaluate the network performance on an additional test set. To load additional test data to evaluate the network with, in the Test section, click Test. Generate plots to analyze the additional test results.

Generate Code

Select Generate Code > Generate Simple Training Script to create MATLAB code to reproduce the previous steps from the command line. Creating MATLAB code can be helpful if you want to learn how to use the command-line functionality of the toolbox to customize the training process. In Cluster Data Using Command-Line Functions, you will investigate the generated scripts in more detail.

Export Network

You can export your trained network to the workspace or Simulink®. You can also deploy the network with MATLAB Compiler™ tools and other MATLAB code generation tools. To export your trained network and results, select Export Model > Export to Workspace.

Cluster Data Using Command-Line Functions

The easiest way to learn how to use the command-line functionality of the toolbox is to generate scripts from the apps, and then modify them to customize the network training. As an example, look at the simple script that was created in the previous section using the Neural Net Clustering app.

% Solve a Clustering Problem with a Self-Organizing Map
% Script generated by Neural Clustering app
% Created 21-May-2021 10:15:01
%
% This script assumes these variables are defined:
%
%   irisInputs - input data.

x = irisInputs;

% Create a Self-Organizing Map
dimension1 = 10;
dimension2 = 10;
net = selforgmap([dimension1 dimension2]);

% Train the Network
[net,tr] = train(net,x);

% Test the Network
y = net(x);

% View the Network
view(net)

% Plots
% Uncomment these lines to enable various plots.
%figure, plotsomtop(net)
%figure, plotsomnc(net)
%figure, plotsomnd(net)
%figure, plotsomplanes(net)
%figure, plotsomhits(net,x)
%figure, plotsompos(net,x)

You can save the script and then run it from the command line to reproduce the results of the previous training session. You can also edit the script to customize the training process. In this case, follow each step in the script.

Select Data

The script assumes that the predictors are already loaded into the workspace. If the data is not loaded, you can load it as follows:

load iris_dataset

This command loads the predictors irisInputs into the workspace.

This data set is one of the sample data sets that is part of the toolbox. For information about the data sets available, see Sample Data Sets for Shallow Neural Networks. You can also see a list of all available data sets by entering the command help nndatasets. You can load the variables from any of these data sets using your own variable names. For example, the command

x = irisInputs;

will load the iris flower predictors into the array x.

Create Network

Create a network. For this example, you use a self-organizing map (SOM). This network has one layer, with the neurons organized in a grid. For more information, see Cluster with Self-Organizing Map Neural Network. When creating the network with selforgmap, you specify the number of rows and columns in the grid.

dimension1 = 10;
dimension2 = 10;
net = selforgmap([dimension1 dimension2]);

Train Network

Train the network. The SOM network uses the default batch SOM algorithm for training.

[net,tr] = train(net,x);

During training, the training window opens and displays the training progress. You can interrupt training at any point by clicking the stop button .

Test Network

Test the network. After the network has been trained, you can use it to compute the network outputs.

y = net(x);

View Network

View the network diagram.

view(net)

Analyze Results

For SOM training, the weight vector associated with each neuron moves to become the center of a cluster of input vectors. In addition, neurons that are adjacent to each other in the topology should also move close to each other in the input space, therefore it is possible to visualize a high-dimensional inputs space in the two dimensions of the network topology. The default SOM topology is hexagonal; to view it, enter the following commands.

figure, plotsomtop(net)

In this figure, each of the hexagons represents a neuron. The grid is 10-by-10, so there are a total of 100 neurons in this network. There are four features in each input vector, so the input space is four-dimensional. The weight vectors (cluster centers) fall within this space.

Because this SOM has a two-dimensional topology, you can visualize in two dimensions the relationships among the four-dimensional cluster centers. One visualization tool for the SOM is the weight distance matrix (also called the U-matrix).

To view the U-matrix, click SOM Neighbor Distances in the training window.

In this figure, the blue hexagons represent the neurons. The red lines connect neighboring neurons. The colors in the regions containing the red lines indicate the distances between neurons. The darker colors represent larger distances, and the lighter colors represent smaller distances. A band of dark segments crosses the map. The SOM network appears to have clustered the flowers into two distinct groups.

Next Steps

To get more experience in command-line operations, try some of these tasks:

• During training, open a plot window (such as the SOM weight position plot) and watch it animate.

• Plot from the command line with functions such as plotsomhits, plotsomnc, plotsomnd, plotsomplanes, plotsompos, and plotsomtop.