Sequence-to-Sequence Regression Using Deep Learning
This example shows how to predict the remaining useful life (RUL) of engines by using deep learning.
To train a deep neural network to predict numeric values from time series or sequence data, you can use a long short-term memory (LSTM) network.
This example uses the Turbofan Engine Degradation Simulation Data Set as described in [1]. The example trains an LSTM network to predict the remaining useful life of an engine (predictive maintenance), measured in cycles, given time series data representing various sensors in the engine. The training data contains simulated time series data for 100 engines. Each sequence varies in length and corresponds to a full run to failure (RTF) instance. The test data contains 100 partial sequences and corresponding values of the remaining useful life at the end of each sequence.
The data set contains 100 training observations and 100 test observations.
Download Data
Download and unzip the Turbofan Engine Degradation Simulation data set.
Each time series of the Turbofan Engine Degradation Simulation data set represents a different engine. Each engine starts with unknown degrees of initial wear and manufacturing variation. The engine is operating normally at the start of each time series, and develops a fault at some point during the series. In the training set, the fault grows in magnitude until system failure.
The data contains a ZIP-compressed text files with 26 columns of numbers, separated by spaces. Each row is a snapshot of data taken during a single operational cycle, and each column is a different variable. The columns correspond to the following:
Column 1 – Unit number
Column 2 – Time in cycles
Columns 3–5 – Operational settings
Columns 6–26 – Sensor measurements 1–21
Create a directory to store the Turbofan Engine Degradation Simulation data set.
dataFolder = fullfile(tempdir,"turbofan"); if ~exist(dataFolder,"dir") mkdir(dataFolder); end
Download and extract the Turbofan Engine Degradation Simulation data set.
filename = matlab.internal.examples.downloadSupportFile("nnet","data/TurbofanEngineDegradationSimulationData.zip"); unzip(filename,dataFolder)
Prepare Training Data
Load the data using the function processTurboFanDataTrain attached to this example. The function processTurboFanDataTrain extracts the data from filenamePredictors and returns the cell arrays XTrain and TTrain, which contain the training predictor and response sequences.
filenamePredictors = fullfile(dataFolder,"train_FD001.txt");
[XTrain,TTrain] = processTurboFanDataTrain(filenamePredictors);Remove Features with Constant Values
Features that remain constant for all time steps can negatively impact the training. Find the columns of data that have the same minimum and maximum values, and remove them.
XTrainConcatenatedTimesteps = cat(1,XTrain{:});
m = min(XTrainConcatenatedTimesteps,[],1);
M = max(XTrainConcatenatedTimesteps,[],1);
idxConstant = M == m;
for i = 1:numel(XTrain)
XTrain{i}(:,idxConstant) = [];
endView the number of remaining features in the sequences.
numFeatures = size(XTrain{1},2)numFeatures = 17
Normalize Training Predictors
Normalize the training predictors to have zero mean and unit variance. To calculate the mean and standard deviation over all observations, concatenate the sequence data horizontally.
XTrainConcatenatedTimesteps = cat(1,XTrain{:});
mu = mean(XTrainConcatenatedTimesteps,1);
sig = std(XTrainConcatenatedTimesteps,0,1);
for i = 1:numel(XTrain)
XTrain{i} = (XTrain{i} - mu) ./ sig;
endClip Responses
To learn more from the sequence data when the engines are close to failing, clip the responses at the threshold 150. This makes the network treat instances with higher RUL values as equal.
thr = 150; for i = 1:numel(TTrain) TTrain{i}(TTrain{i} > thr) = thr; end
This figure shows the first observation and the corresponding clipped response.

Prepare Data for Padding
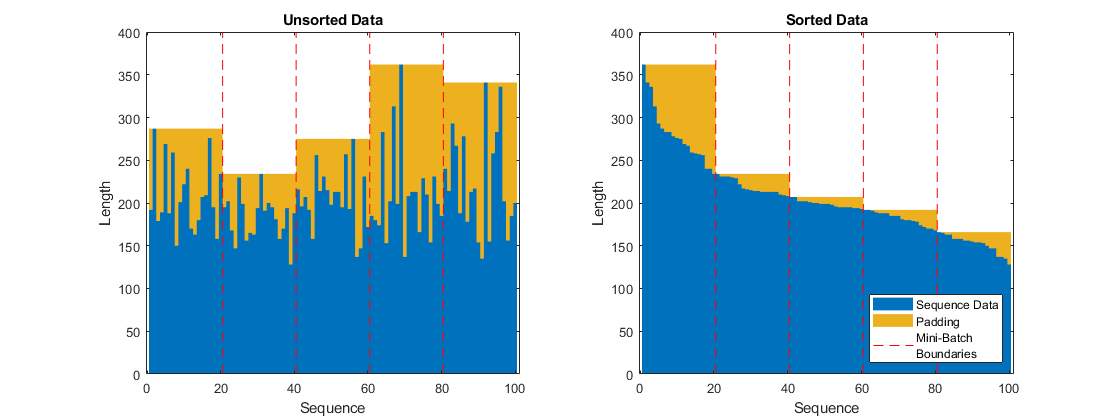
To minimize the amount of padding added to the mini-batches, sort the training data by sequence length. Then, choose a mini-batch size which divides the training data evenly and reduces the amount of padding in the mini-batches.
Sort the training data by sequence length.
for i=1:numel(XTrain) sequence = XTrain{i}; sequenceLengths(i) = size(sequence,1); end [sequenceLengths,idx] = sort(sequenceLengths,"descend"); XTrain = XTrain(idx); TTrain = TTrain(idx);
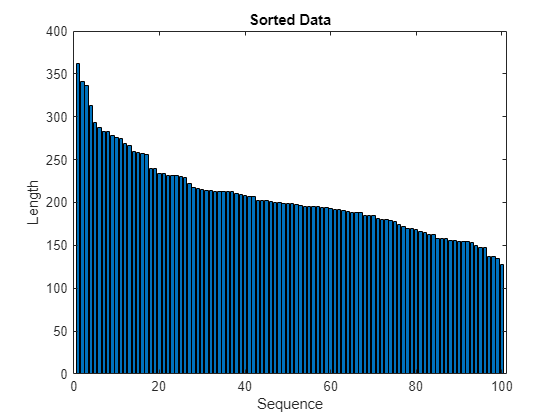
View the sorted sequence lengths in a bar chart.
figure bar(sequenceLengths) xlabel("Sequence") ylabel("Length") title("Sorted Data")
Choose a mini-batch size which divides the training data evenly and reduces the amount of padding in the mini-batches. This figure illustrates the padding added to the unsorted and sorted sequences for mini-batches of size 20.
Define Network Architecture
Define the network architecture. Create an LSTM network that consists of an LSTM layer with 200 hidden units, followed by a fully connected layer of size 50 and a dropout layer with dropout probability 0.5.
numResponses = size(TTrain{1},2);
numHiddenUnits = 200;
layers = [ ...
sequenceInputLayer(numFeatures)
lstmLayer(numHiddenUnits,OutputMode="sequence")
fullyConnectedLayer(50)
dropoutLayer(0.5)
fullyConnectedLayer(numResponses)];Specify the training options. Train for 60 epochs with mini-batches of size 20 using the solver "adam". Specify the learning rate 0.01. To prevent the gradients from exploding, set the gradient threshold to 1. To keep the sequences sorted by length, set the Shuffle option to "never". Display the training progress in a plot and monitor the root mean squared error (RMSE) metric.
maxEpochs = 60; miniBatchSize = 20; options = trainingOptions("adam", ... MaxEpochs=maxEpochs, ... MiniBatchSize=miniBatchSize, ... InitialLearnRate=0.01, ... GradientThreshold=1, ... Shuffle="never", ... Metrics="rmse", ... Plots="training-progress", ... Verbose=0);
Train the Network
Train the neural network using the trainnet function. For regression, use mean squared error loss. By default, the trainnet function uses a GPU if one is available. Training on a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the trainnet function uses the CPU. To specify the execution environment, use the ExecutionEnvironment training option.
net = trainnet(XTrain,TTrain,layers,"mse",options);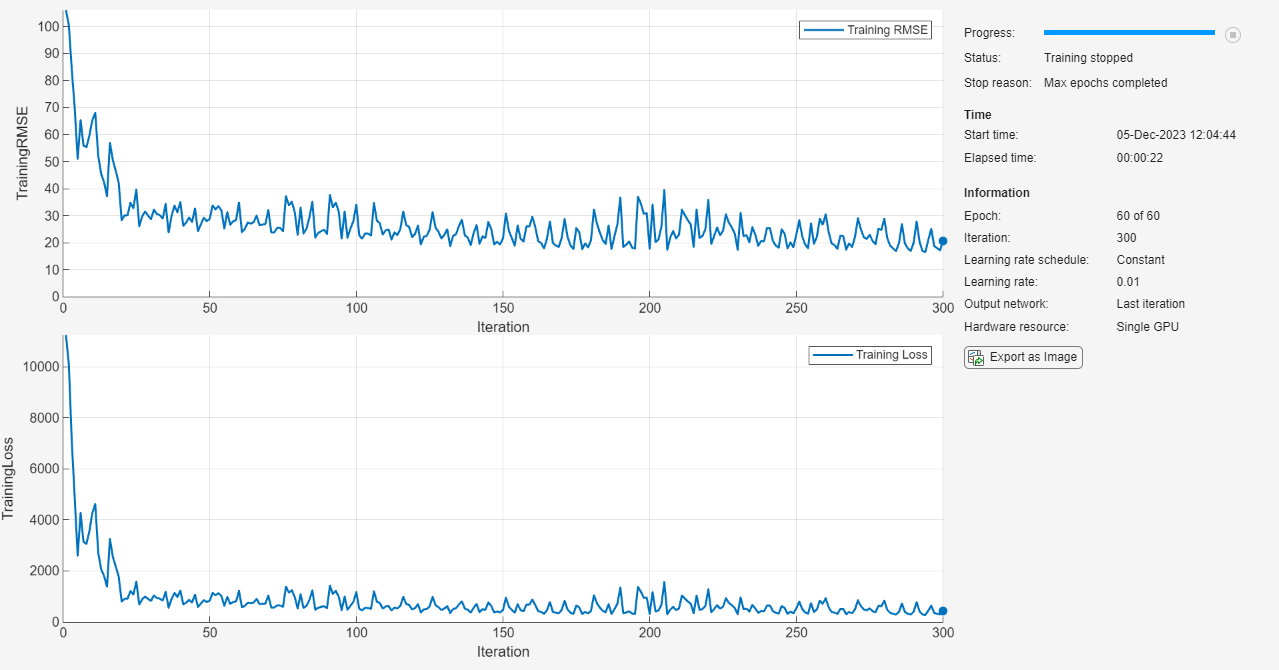
Test the Network
Prepare the test data using the function processTurboFanDataTest attached to this example. The function processTurboFanDataTest extracts the data from filenamePredictors and filenameResponses and returns the cell arrays XTest and TTest, which contain the test predictor and response sequences, respectively.
filenamePredictors = fullfile(dataFolder,"test_FD001.txt"); filenameResponses = fullfile(dataFolder,"RUL_FD001.txt"); [XTest,TTest] = processTurboFanDataTest(filenamePredictors,filenameResponses);
Remove features with constant values using idxConstant calculated from the training data. Normalize the test predictors using the same parameters as in the training data. Clip the test responses at the same threshold used for the training data.
for i = 1:numel(XTest) XTest{i}(:,idxConstant) = []; XTest{i} = (XTest{i} - mu) ./ sig; TTest{i}(TTest{i} > thr) = thr; end
Make predictions using the neural network. To make predictions with multiple observations, use the minibatchpredict function. The minibatchpredict function automatically uses a GPU if one is available. Using a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements. Otherwise, the function uses the CPU. To prevent the function from adding padding to the data, specify the mini-batch size 1. To return predictions in a cell array, set UniformOutput to false.
YTest = minibatchpredict(net,XTest,MiniBatchSize=1,UniformOutput=false);
The LSTM network makes predictions on the partial sequence one time step at a time. At each time step, the network predicts using the value at this time step, and the network state calculated from the previous time steps only. The network updates its state between each prediction. The minibatchpredict function returns a sequence of these predictions. The last element of the prediction corresponds to the predicted RUL for the partial sequence.
Alternatively, you can make predictions one time step at a time by using predict and updating the network State property. This is useful when you have the values of the time steps arriving in a stream. Usually, it is faster to make predictions on full sequences when compared to making predictions one time step at a time. For an example showing how to forecast future time steps by updating the network between single time step predictions, see Time Series Forecasting Using Deep Learning.
Visualize some of the predictions in a plot.
idx = randperm(numel(YTest),4); figure for i = 1:numel(idx) subplot(2,2,i) plot(TTest{idx(i)},"--") hold on plot(YTest{idx(i)},".-") hold off ylim([0 thr + 25]) title("Test Observation " + idx(i)) xlabel("Time Step") ylabel("RUL") end legend(["Test Data" "Predicted"],Location="southeast")

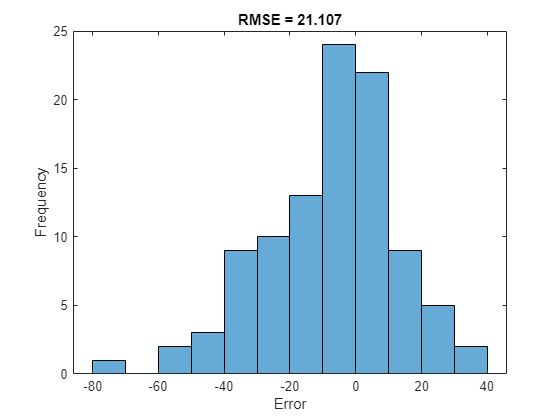
For a given partial sequence, the predicted current RUL is the last element of the predicted sequences. Calculate the root-mean-square error (RMSE) of the predictions, and visualize the prediction error in a histogram.
for i = 1:numel(TTest) TTestLast(i) = TTest{i}(end); YTestLast(i) = YTest{i}(end); end figure rmse = sqrt(mean((YTestLast - TTestLast).^2))
rmse = single
21.1070
histogram(YTestLast - TTestLast) title("RMSE = " + rmse) ylabel("Frequency") xlabel("Error")
References
Saxena, Abhinav, Kai Goebel, Don Simon, and Neil Eklund. "Damage propagation modeling for aircraft engine run-to-failure simulation." In Prognostics and Health Management, 2008. PHM 2008. International Conference on, pp. 1-9. IEEE, 2008.
See Also
trainnet | trainingOptions | dlnetwork | testnet | minibatchpredict | scores2label | predict | lstmLayer | sequenceInputLayer
See Also
Topics
- Sequence-to-One Regression Using Deep Learning
- Sequence Classification Using Deep Learning
- Time Series Forecasting Using Deep Learning
- Sequence-to-Sequence Classification Using Deep Learning
- Long Short-Term Memory Neural Networks
- Deep Learning in MATLAB
- Choose Training Configurations for LSTM Using Bayesian Optimization