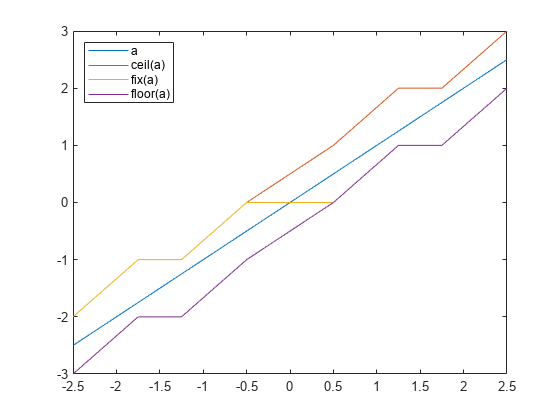floor
Round toward negative infinity
Syntax
Description
Examples
Input Arguments
Algorithms
yandahave the samefimathobject andDataTypeproperty.When the
DataTypeproperty ofaissingle,double, orboolean, thenumerictypeofyis the same as that ofa.When the fraction length of
ais zero or negative,ais already an integer, and thenumerictypeofyis the same as that ofa.When the fraction length of
ais positive, the fraction length ofyis0, its sign is the same as that ofa, and its word length is the difference between the word length and the fraction length ofa, plus one bit. Ifais signed, then the minimum word length ofyis2. Ifais unsigned, then the minimum word length ofyis1.
Extended Capabilities
Version History
Introduced in R2008a
See Also
ceil | convergent | fix | nearest | round