Build Fuzzy Systems Using Custom Functions
When you build a fuzzy inference system (FIS), you can replace the built-in membership functions (MFs) or inference functions with custom functions. You can create a FIS that uses these custom functions in the Fuzzy Logic Designer app and at the MATLAB® command line.
For more information on creating a FIS, see Build Fuzzy Systems Using Fuzzy Logic Designer and Build Fuzzy Systems at the Command Line.
Define Custom Membership Functions
You can create custom membership functions and use them in the fuzzy inference process. The values of these functions must lie between 0 and 1. For more information on the properties of membership functions, see Membership Functions.
When you create a custom membership function, you must save it in your current working folder or on the MATLAB path. You can then design a FIS that uses the custom membership function at the command line or in the Fuzzy Logic Designer app.
The following is an example of a multistep custom membership function
custmf1, which depends on eight parameters between 0
and 10.
% Function to generate a multi-step custom membership function % using 8 parameters for the input argument x function out = custmf1(x,params) for i = 1:length(x) if x(i) < params(1) y(i) = params(1); elseif x(i) < params(2) y(i) = params(2); elseif x(i) < params(3) y(i) = params(3); elseif x(i) < params(4) y(i) = params(4); elseif x(i) < params(5) y(i) = params(5); elseif x(i) < params(6) y(i) = params(6); elseif x(i) < params(7) y(i) = params(7); elseif x(i) <= params(8) y(i) = params(8); else y(i) = 0; end end % Scale the output to the range [0,1]. out = 0.1*y'; end
Specify Custom Membership Functions Using Fuzzy Logic Designer
Since R2022b
To use a custom membership function when designing a FIS using the Fuzzy Logic Designer app, first select the corresponding variable in the System Browser. Then, in the Add Components gallery, click MF.

The app adds a default triangular membership function to the selected variable.
In the Property Editor:
In the Range field, specify an input range that matches the expected range of your membership function.
In the Name column, specify a name for the membership function.
In the Type column, specify the name of the custom membership function.
In the Parameters column, enter the membership function parameters.
![Property Editor showing an input range of [1,10] and a custom MF of type custmf1 with parameters [0 1 2 4 6 8 9 10]](app-custom-configure-mf.png)
To verify the appearance of your membership function, select the membership function in the System Browser and open the Membership Function Editor.

The following features are not supported for custom membership functions:
Interactively adjusting the parameters of a custom membership function in the Membership Function Editor.
Automatically distributing custom membership functions across a variable range.
Define Custom Inference Functions
Depending on the type of FIS you design, you can replace the built-in AND, OR, implication, aggregation, and defuzzification inference methods with custom functions. For each type of inference function, the following table lists the FIS objects that support using custom functions.
| Inference Function | Supported FIS Objects |
|---|---|
| AND | All FIS objects |
| OR | |
| Implication |
|
| Aggregation | |
| Defuzzification | Type-1 Mamdani FIS |
| Type-reduction |
|
When you create a custom inference function, you must save it in your current working folder or on the MATLAB path. You can then design a FIS that uses the custom inference function at the command line or in the Fuzzy Logic Designer app.
Create Custom AND and OR Functions
The custom AND and OR inference functions must operate column-wise on a matrix in the
same way as the MATLAB functions max, min, and
prod. For example:
For a row or column vector
x,minreturns the minimum element.x = [1 2 3 4]; min(x)
ans = 1For a matrix
x,minreturns a row vector containing the minimum element from each column.x = [1 2 3 4;5 6 7 8;9 10 11 12]; min(x)
For N-D matrices,ans = 1 2 3 4minoperates along the first non-singleton dimension.For two arrays,
xandy,minreturns an array that is same size as the larger ofxorywith the minimum elements fromxory. Either of the input arguments can be a scalar.x = [1 2; 3 4]; y = [2 2; 2 2]; min(x,y)
ans = 1 2 2 2
In Fuzzy Logic Toolbox™ software:
AND inference functions perform an element-by-element matrix operation similar to the command
min(x,y).OR inference functions perform an element-by-element matrix operation similar to the command
max(x,y).
Create Custom Implication Functions
Custom implication functions must operate in the same way as the MATLAB functions max, min, and
prod. Your custom implication function must be a
T-norm fuzzy intersection operation. For more information, see Additional Fuzzy Operators.
An implication function must support either one or two inputs because the software calls the function in two ways.
To calculate the output fuzzy set values using the firing strength of all the rules and the corresponding output membership functions. In this case, the software calls the implication function using two inputs as follows.
impvals = customimp(w,outputmf)
w— Firing strength of multiple rules, specified as an Nr-by-Ns matrix. Here, Nr is the number of rules and Ns is the number of samples of the output membership functions.w(:,j) = w(:,1)for all j.w(i,1)is the firing strength of the ith rule.outputmf— Output membership function values, specified as an Nr-by-Ns matrix.outputmf(i,:)contains the data of the ith output membership function.
To calculate the output fuzzy value using the firing strength of a single rule and the corresponding output membership function, for a given sample. In this case, the software calls the implication function using one input, similar to the following example.
impval = customimp([w outputmf])
wandoutputmfare scalar values representing the firing strength of a rule and the corresponding output membership function value, for a given sample.
The following is an example of a bounded product custom implication function with binary mapping [1].
function y = customimp(x1,x2) if nargin == 1 % x1 assumed to be nonempty column vector or matrix. minVal = zeros(1,size(x1,2)); y = ones(1,size(x1,2)); for i = 1:size(x1,1) y = max(minVal,sum([y;x1(i,:)])-1); end else % x1 and x2 assumed to be nonempty matrices. minVal = zeros(1,size(x1,2)); y = zeros(size(x1)); for i = 1:size(x1,1) y(i,:) = max(minVal,sum([x1(i,:);x2(i,:)])-1); end end end
Note
Custom implication functions are not supported for Sugeno systems.
Create Custom Aggregation Functions
Custom aggregation functions must operate in the same way as the MATLAB functions max, min, and
prod and must be of the form y = customagg(x).
Your custom implication function must be a T-conorm
(S-norm) fuzzy intersection operation. For more information, see
Additional Fuzzy Operators.
x is an
Nv-by-Nr
matrix, which is the list of truncated output functions returned by the implication method
for each rule. Nv is the number of output
variables and Nr is the number of rules. The
output of the aggregation method is one fuzzy set for each output variable.
The following is an example of a bounded sum custom aggregation function with binary mapping [1].
function y = customagg(x) maxVal = ones(1,size(x,2)); y = zeros(1,size(x,2)); for i = 1:size(x,1) y = min(maxVal,sum([y;x(i,:)])); end end
Note
Custom aggregation functions are not supported for Sugeno systems.
Create Custom Defuzzification Functions
Custom defuzzification functions must be of the form y =
customdefuzz(x,ymf), where x is the vector of values in the
membership function input range and ymf contains the values of the
membership function for each x value.
The following is an example of a custom defuzzification function.
function defuzzfun = customdefuzz(x,ymf) total_area = sum(ymf); defuzzfun = sum(ymf.*x)/total_area; end
Note
Custom defuzzification functions are not supported for Sugeno systems.
Create Custom Type-Reduction Function
For type-2 fuzzy inference systems, you can specify a custom type-reduction function.
This function must be of the form y = customtr(x,umf,lmf), where
x is the vector of values in the membership function input range.
umf and lmf are the respective values of the upper
and lower membership function for each x value. The output
y is a two-element row vector of centroids
[cL,cR].
For more information on type reduction, see Type-2 Fuzzy Inference Systems.
By default, type-2 Sugeno systems support only a weighted average form of type reduction. The following custom type-reduction function implements a weighted sum form of type reduction for a Sugeno system.
function y = customtr(x,umf,lmf) y = zeros(1,2); y(1) = sum(x.*umf); y(2) = sum(x.*lmf); end
Specify Custom Inference Functions Using Fuzzy Logic Designer
Since R2022b
To use custom inference functions when designing a FIS using the Fuzzy Logic Designer app, first select the FIS in the System Browser. Then, in the Property Editor, enter the name of the custom function in the corresponding inference function field.
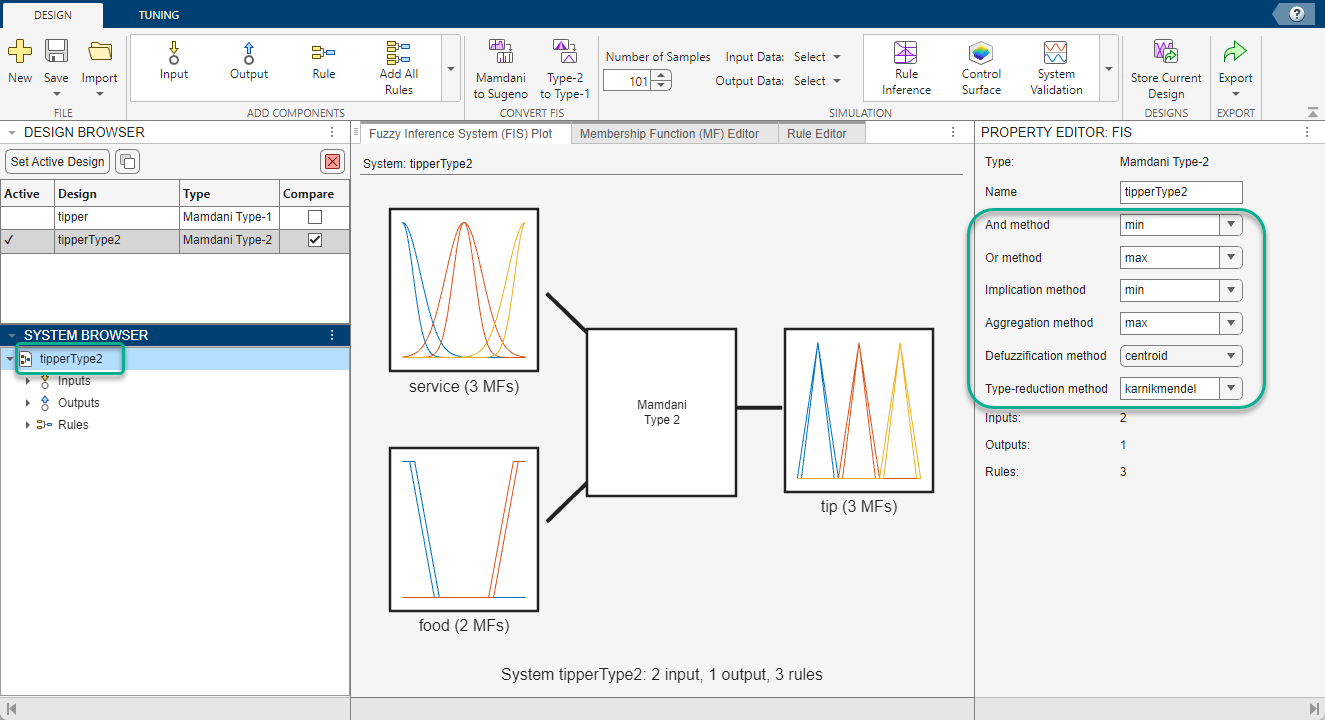
This table shows the Property Editor field for each type of inference function.
| Inference Function | Property Editor Field |
|---|---|
| AND | And method |
| OR | Or method |
| Implication | Implication method |
| Aggregation | Aggregation method |
| Defuzzification | Defuzzification method |
| Type-reduction | Type-reduction method |
Specify Custom Inference Functions at Command Line
To use custom inference functions when designing a FIS at the MATLAB command line, set the corresponding FIS object property to the custom
inference function name. For example, the following command sets the aggregation function
of FIS myFIS to the customagg function.
myFIS.AggregationMethod = "customagg";This table shows the FIS object property for each type of inference function.
| Inference Function | FIS Object Property |
|---|---|
| AND | AndMethod |
| OR | OrMethod |
| Implication | ImplicationMethod |
| Aggregation | AggregationMethod |
| Defuzzification | DefuzzificationMethod |
| Type-reduction | TypeReductionMethod |
Use Custom Functions in Code Generation
You can use custom functions in fuzzy inference systems for which you generate code. For more information on code generation for fuzzy systems, see Deploy Fuzzy Inference Systems.
If you use a nondouble data type for your generated code, you must propagate the data
type from the input arguments of your custom function to the output argument. For example,
the following custom aggregation function maintains the data type of x in
y using the ones and zeros
functions with the 'like' argument.
function y = customagg(x) %#codegen maxVal = ones(1,size(x,2),'like',x); y = zeros(1,size(x,2),'like',x); for i = 1:size(x,1) y = min(maxVal,sum([y;x(i,:)])); end end
For more information on writing functions that support C/C++ code generation, see MATLAB Programming for Code Generation (MATLAB Coder).
References
[1] Mizumoto, Masaharu. "Pictorial Representations of Fuzzy Connectives, Part II: Cases of Compensatory Operators and Self-Dual Operators." Fuzzy Sets and Systems 32, no. 1 (August 1989): 45–79. https://doi.org/10.1016/0165-0114(89)90087-0.