Tune Fuzzy Robot Obstacle Avoidance System Using Custom Cost Function
This example shows how to tune a fuzzy inference system (FIS) using a custom cost function. The example requires Global Optimization Toolbox software.
Problem Description
In this example, you use a custom cost function to learn robot navigation in a simulation environment. The goal of the navigation task is to reach a specified target while avoiding obstacles. The direction to the target is represented as a unit force vector () directed from the robot to a target location. The obstacle avoidance direction is represented by a unit force vector () directed towards the robot from the closest obstacle location.

The robot, target, and obstacle are shown as circles with 0.5 m radius in the 25 m x 25 m simulation environment. The navigation task is to combine the force vectors such that the direction of the resultant force vector provides a collision-free direction for the robot.
, where
This example assumes a robot with differential kinematics for the simulation. In other words, the robot can rotate on its center without any constraints. However, to avoid sharp turns, the change per time step in the robot direction is limited to . Therefore, if the current robot heading direction is , the next heading direction is calculated as:
.
The weight of the force vector is calculated using function :
where
is the ratio of the robot-to-obstacle distance () and the robot-to-target-distance ()
is the absolute difference between the target and obstacle directions with respect to the robot
To achieve the navigation task, the function must generate high values, that is, focus on avoiding the obstacle when:
Both the target and obstacle directions from the robot are similar ( is low)
The obstacle is closer to the robot than the target ( is low).
Otherwise, must generate low values, that is, focus on reaching the target.
The goal of this example is to design a FIS that learns fuzzy rules and optimizes the FIS parameters to model the function for collision-free robot navigation in the simulation environment.
Assumptions
The following assumptions apply for the robot simulation:
The robot can perfectly localize in the simulation environment; that is, the robot knows its current position in the simulation environment.
The robot is equipped with perfect sensors to identify the obstacle and determine its location.
The robot has no dynamic constraints; that is, the robot can rotate and move as commanded without any mechanical constraints. To avoid sharp turns, a soft constraint is imposed on rotation, which limits the change per time step in the robot heading to .
The robot runs with a fixed speed. You can include additional fuzzy systems to control the robot speed. For simplicity, this example uses a fixed speed for the robot.
Construct Fuzzy System
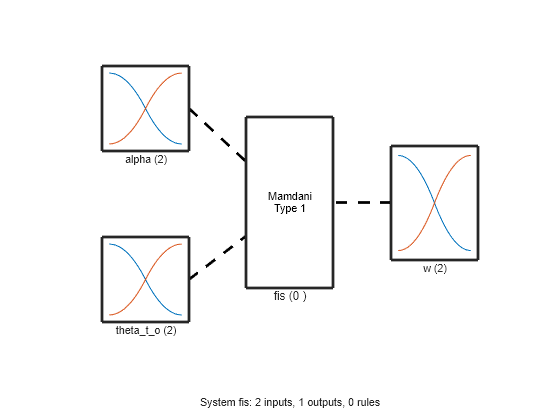
To model function , construct a FIS as shown in the following figure. For this example, use a Mamdani FIS.

fisin = mamfis;
Add the following two inputs as shown in the previous figure.
— Ratio of distances, robot-to-obstacle / robot-to-target
— Difference between target and obstacle directions
Set the range of the first input to [0,2], which indicates that contributes to obstacle avoidance when the obstacle distance is less than or equal to twice the target distance.
Set the range of the second input to [0,pi/2], which indicates that contributes to obstacle avoidance when the difference between the target and obstacle directions is less than or equal to pi/2.
fisin = addInput(fisin,[0 2],Name="alpha"); fisin = addInput(fisin,[0 pi/2],Name="theta_t_o");
To minimize the number of rules, which corresponds to the number of combinations of input membership functions, add two membership functions (MFs) to each input. To generate similar membership values beyond the input ranges, use zmf (Z-shaped curve membership function) and smf (S-shaped curve membership function) MFs. The tuning process optimizes the input MF parameter values.
Add membership functions to the first input.
fisin = addMF(fisin,"alpha","zmf",[0 2],Name="low"); fisin = addMF(fisin,"alpha","smf",[0 2],Name="high");
Add membership functions to the second input.
fisin = addMF(fisin,"theta_t_o","zmf",[0 pi/2],Name="low"); fisin = addMF(fisin,"theta_t_o","smf",[0 pi/2],Name="high");
Add an output to the FIS or the obstacle force vector weight, restricting the weight values to the range [0,1].
fisin = addOutput(fisin,[0 1],Name="w");Add two MFs to the output. You can add more MFs to the output for finer granularity of output values. However, doing so increases the number of tuning parameters. The output MFs also use zmf and smf to generate similar membership values beyond the input ranges. The tuning process optimizes the output MF parameter values.
fisin = addMF(fisin,"w","zmf",[0 1],Name="low"); fisin = addMF(fisin,"w","smf",[0 1],Name="high");
View the FIS structure. Initially, the FIS has zero rules. The tuning process finds rules for the fuzzy system.
figure plotfis(fisin)
Learn Rules and Optimize FIS Parameters
Since you do not have training data for this example, you simulate the robot navigation using a custom cost function. The tuning process uses this custom cost function when optimizing the FIS parameters.
For parameter optimization, obtain the parameter settings from the FIS.
[in,out] = getTunableSettings(fisin);
Next, create tuning options with OptimizationType set to learning. This example uses the genetic algorithm (ga) optimization method for the tuning process. To improve the speed of the tuning process, set the UseParallel option to true, which requires Parallel Computing Toolbox™ software. If you do not have Parallel Computing Toolbox software, set UseParallel to false.
options = tunefisOptions(Method="ga",OptimizationType="learning");
Set the population size of the genetic algorithm to 200. The larger population size increases the probability of generating a better solution in fewer generations.
options.MethodOptions.PopulationSize = 200;
Set the maximum number of generations to 25. To tune the parameters further, you can set a higher number of generations. However, doing so increases the duration of the tuning process and can overtune the parameter values.
options.MethodOptions.MaxGenerations = 25;
Set the locations of the obstacle, target, and robot for the training environments. Set the initial heading of the robot to pi/2 for the training environment. To learn navigation both with and without obstacle avoidance on the way to the target location, use two training tasks with different obstacle locations.
trnObstacle = [3 12;13 18]; trnTarget = [13 22;13 22]; trnRobot = [13 2 pi/2;13 2 pi/2;]; showSimulationEnvironmentsForTraining(trnObstacle,trnTarget,trnRobot)
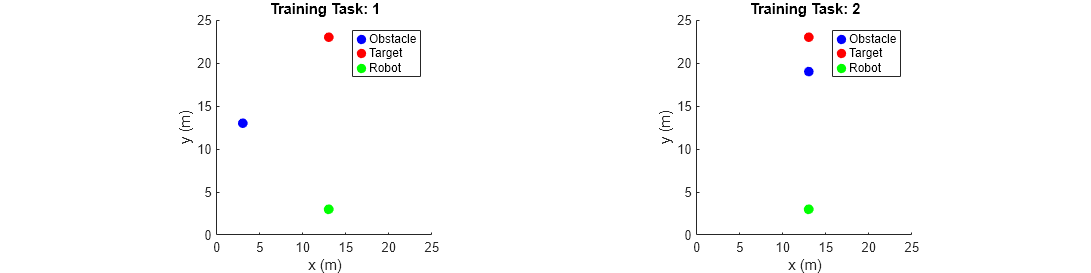
Specify the custom cost function using a function handle.
costFunction = @(fis)navigationCostFcn(fis,trnObstacle,trnTarget,trnRobot);
In the cost function, the robot navigation is simulated in the training environments using each FIS from the population. Each navigation task is run for 100 iterations, where each iteration is equivalent to a decision cycle of length 1 s. The robot uses a fixed speed of 0.5 m/s throughout the navigation task. For more simulation details, see the getNavigationResults function.
function cost = navigationCostFcn(fis,obstacle,target,robot)
cost = 0;
for i = 1:size(obstacle,1)
results = getNavigationResults(fis,obstacle(i,:),target(i,:),robot(i,:));
cost = cost + getNavigationCost(results);
end
end
The cost of each navigation task is the total distance traveled by the robot. If the robot does not reach the target or collides with the obstacle, a high cost value (200) is assigned for the simulation.
function cost = getNavigationCost(results)
if results.notSafe || ~results.reachedTarget
cost = 200;
else
cost = results.travelledDistance;
end
end
Since genetic algorithm optimization uses random search, to obtain reproducible results, initialize the random number generator to its default configuration.
rng("default")Learning rules using the tunefis function takes approximately 10 minutes. For this example, enable tuning by setting runtunefis to true. To load pretrained results without running tunefis, you can set runtunefis to false.
runtunefis = false;
Tune the FIS using the specified training environments and tuning options.
if runtunefis fisout = tunefis(fisin,[in;out],costFunction,options); %#ok<UNRCH> else tunedfis = load("tunedfisnavigation.mat"); fisout = tunedfis.fisout; end
The tuned FIS produces the following robot trajectories in the simulation environments.
showNavigationTrajectories(fisout,trnObstacle,trnTarget,trnRobot)

In the first case, the robot reaches the target with minimum distance since the obstacle is not on the path to the target. In the second case, the robot successfully avoids the obstacle and reaches the target.
View the structure of the tuned FIS, fisout.
figure plotfis(fisout)
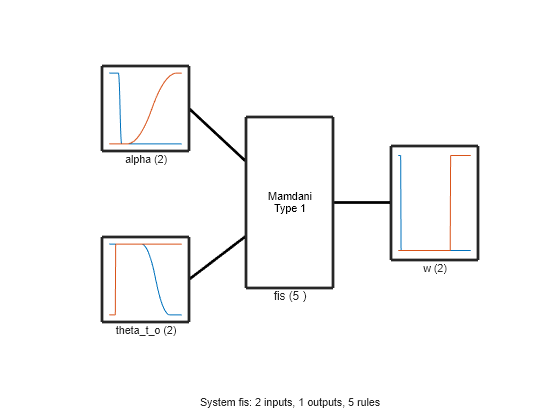
The tuning process produces a set of new rules for the FIS.
fisout.Rules
ans =
1×5 fisrule array with properties:
Description
Antecedent
Consequent
Weight
Connection
Details:
Description
____________________________________________
1 "alpha==low & theta_t_o==high => w=low (1)"
2 "alpha==low & theta_t_o==low => w=high (1)"
3 "theta_t_o==high => w=low (1)"
4 "alpha==high & theta_t_o==high => w=low (1)"
5 "alpha==low => w=low (1)"
The rules are described as follows with respect to the expected behaviors of :
Rule 1 is consistent with the expected behavior of . When the obstacle is not located in front of the robot on the way to the target ( is high) and the obstacle is close ( is low), this rule produces low weight values.
Rule 4 is also consistent with the expected behavior of . When the obstacle is not located in front of the robot on the way to the target ( is high) and the obstacle is farther away ( is high), this rule produces low weight values.
Rule 3 generates low weight values when the obstacle is not located in front of the robot ( is high), irrespective of the obstacle distance. This rule covers the conditions for both rule 1 and rule 4. Therefore, rules 1 and 4 are redundant and can be removed.
Rule 2 is also consistent with the expected behavior of . When the obstacle is close to the robot ( is low) and is located in front of the robot on the way to the target ( is low), this rule produces high weight values for the obstacle avoidance task.
Rule 5 generates low weight values when the obstacle distance is low. This rule contradicts rule 2 when is low. In this case, the output of rule 5 does not contribute to the final output due to the high output values of rule 2. Therefore, rule 5 can also be removed.
Remove the redundant rules.
fisoutpruned = fisout; fisoutpruned.Rules([1 4 5]) = []; fisoutpruned.Rules
ans =
1×2 fisrule array with properties:
Description
Antecedent
Consequent
Weight
Connection
Details:
Description
___________________________________________
1 "alpha==low & theta_t_o==low => w=high (1)"
2 "theta_t_o==high => w=low (1)"
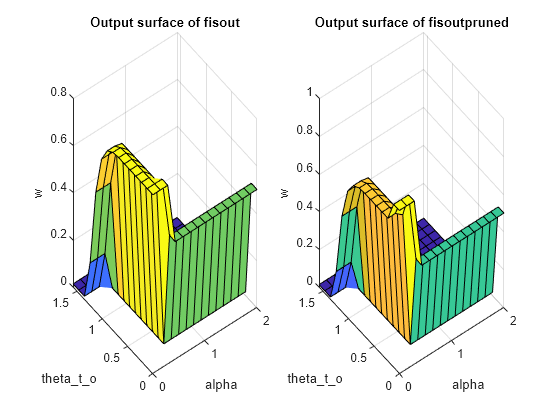
fisout and fisoutpruned generate similar control surfaces. Therefore, only two rules are necessary for obstacle avoidance in the simulation environment.
figure subplot(1,2,1) gensurf(fisout) title("Output surface of fisout") subplot(1,2,2) gensurf(fisoutpruned) title("Output surface of fisoutpruned")
Check Performance
Validate the performance of the tuned FIS with different positions of the obstacle, robot, and target. In the following validation cases, the robot successfully avoids the obstacle to reach the target position using the tuned FIS.
vldObstacle = [13 5;10 10;8 8]; vldRobot = [5 12 0;5 20 -pi/2;19 19 -pi]; vldTarget = [23 12;15 4;5 5]; showNavigationTrajectories(fisoutpruned,vldObstacle,vldTarget,vldRobot)
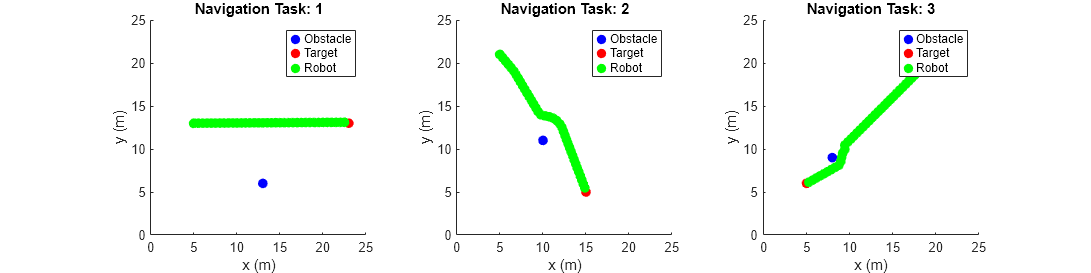
Conclusion
This example uses a custom cost function that simulates robot navigation in different training environments to learn fuzzy rules and optimize the FIS parameter values for collision-free navigation. You can Include more training environments to learn obstacle avoidance in other scenarios, for example narrow corridor and U-shape obstacles. In these scenarios, the robot may need additional navigation subtasks, such as wall following and subtarget (intermediate landmark) reaching, for successful collision-free navigation to the target. Complex environments also require additional terms in the cost calculation for safe navigation. For example, in a narrow corridor the robot should stay in the middle; that is, the distances to the obstacles on the left and right should be the same.
Using a custom cost function with tunefis provides the flexibility of simulating a custom system with custom cost calculation. However, the tradeoff is a lengthy tuning process due to the number of simulations required (for each set of optimized parameter values). Therefore, if possible, to expedite the tuning process, use training data. For instance, the tuning process in this example would run faster if input/output decision data of a human operator was available for tuning the FIS.
Local Functions
function showSimulationEnvironment(obstacle,target,robot,navigationResults) % Show the robot trajectory in the simulation environment. % Radius of the robot, target, and obstacle. radius = 1; % 1m % Use 25mx25m simulation environment. axis([0 25 0 25]); % Set equal aspect ratio. pbaspect([1 1 1]) % Temporary plots to enable legends. hold on plot(robot(1),robot(2)+radius,"ob",LineWidth=radius*1,MarkerFaceColor="b") plot(robot(1),robot(2)+radius,"or",LineWidth=radius*1,MarkerFaceColor="r") plot(robot(1),robot(2)+radius,"og",LineWidth=radius*1,MarkerFaceColor="g") hold off % Draw obstacle. rectangle(Position=[obstacle(1)-0.5*radius obstacle(2)+0.5*radius radius radius], ... Curvature=[1 1],FaceColor="b",EdgeColor="b") % Draw target. rectangle(Position=[target(1)-0.5*radius target(2)+0.5*radius radius radius], ... Curvature=[1 1],FaceColor="r",EdgeColor="r") % Draw robot. rectangle(Position=[robot(1)-0.5*radius robot(2)+0.5*radius radius radius], ... Curvature=[1 1],FaceColor="g",EdgeColor="g") % Add labels, title, and legends. xlabel("x (m)") ylabel("y (m)") title("Simulation Environment for Robot Navigation") legend(["Obstacle" "Target" "Robot"]) % Plot the robot trajectory if specified. if nargin == 4 x = navigationResults.x; y = navigationResults.y; for i = 1:numel(x) rectangle(Position=[x(i)-0.5*radius y(i)+0.5*radius radius radius], ... Curvature=[1 1],FaceColor="g",EdgeColor="g") end end end function showSimulationEnvironmentsForTraining(obstacle,target,robot) % Show simulation environments for training. drawEnvironmentAndShowTrajectory(obstacle,target,robot,"Training Task") end function showNavigationTrajectories(fis,obstacle,target,robot) % Show robot trajectories in the simulation environments. drawEnvironmentAndShowTrajectory(obstacle,target,robot,"Navigation Task",fis) end function drawEnvironmentAndShowTrajectory(obstacle,target,robot,plotTitle,varargin) % Expand figure horizontally to tile the simulation environments. h = figure; h.Position = [h.Position(1:2) 3*h.Position(3) h.Position(4)]; numTasks = size(target,1); % Draw each simulation environment. for i = 1:numTasks o = obstacle(i,:); t = target(i,:); r = robot(i,:); subplot(1,numTasks,i) if ~isempty(varargin) results = getNavigationResults(varargin{1},o,t,r); showSimulationEnvironment(o,t,r,results) else showSimulationEnvironment(o,t,r) end title(plotTitle + ": " + num2str(i)) end end
See Also
tunefis | mamfis | getTunableSettings