Plot Functions for GlobalSearch and MultiStart
What Are Plot Functions?
The PlotFcn field of options specifies one or more
functions that an optimization function calls at each iteration. Plot functions plot
various measures of progress while the algorithm executes. Pass a function handle or
cell array of function handles. The structure of a plot function is the same as the
structure of an output function. For more information on this structure, see OutputFcn.
Plot functions are specialized output functions (see Output Functions for GlobalSearch and MultiStart). There are two predefined plot functions:
@gsplotbestfplots the best objective function value.@gsplotfunccountplots the number of function evaluations.
Plot function windows have Pause and Stop buttons. By default, all plots appear in one window.
To use global plot functions:
Write plot functions using the syntax described in OutputFcn.
Set the
PlotFcnproperty of yourGlobalSearchorMultiStartobject to the function handle of your plot function. You can use multiple plot functions by setting thePlotFcnproperty to a cell array of function handles.
Note
Plot functions do not support the subplot statement, because the plot
function framework manages the axes. To specify multiple subplots, write separate plot
functions and pass them to the solver as a cell array:
options = optimoptions("solvername",PlotFcn={@plot1,@plot2,@plot3});Output functions support subplot, so you can include multiple plots in
one function by using an output function instead of a plot function.
Details of Built-In Plot Functions
The built-in plot functions have characteristics that can surprise you.
@gsplotbestfcan have plots that are not strictly decreasing. This is because early values can result from local solver runs with negative exit flags (such as infeasible solutions). A subsequent local solution with positive exit flag is better even if its function value is higher. Once a local solver returns a value with a positive exit flag, the plot is monotone decreasing.@gsplotfunccountmight not plot the total number of function evaluations. This is becauseGlobalSearchcan continue to perform function evaluations after it calls the plot function for the last time. For more information, see GlobalSearch Algorithm.
MultiStart Plot Function
This example plots the number of local solver runs it takes to obtain a better local minimum for MultiStart. The example also uses a built-in plot function to show the current best function value.
The example problem is the same as in Find Global or Multiple Local Minima, with additional bounds.
The example uses persistent variables to store previous best values. The plot function examines the best function value after each local solver run, available in the bestfval field of the optimValues structure. If the value is not lower than the previous best, the plot function adds 1 to the number of consecutive calls with no improvement and draws a bar chart. If the value is lower than the previous best, the plot function starts a new bar in the chart with value 1. Before plotting, the plot function takes a logarithm of the number of consecutive calls. The logarithm helps keep the plot legible, since some values can be much larger than others.
To store local results using nested functions instead of persistent variables, see Example of a Nested Output Function.
Plot Function Example
This example minimizes the sawtoothxy helper function, which is listed at the end of this example. In general, save your objective function in a file on your MATLAB® path.
The NumberToNextBest custom plot function is attached to this example. In general, save your plot function in a file on your MATLAB path. Here is a listing.
type NumberToNextBestfunction stop = NumberToNextBest(optimValues, state)
persistent bestfv bestcounter
stop = false;
switch state
case 'init'
% Initialize variable to record best function value.
bestfv = [];
% Initialize counter to record number of
% local solver runs to find next best minimum.
bestcounter = 1;
% Create the histogram.
bar(log(bestcounter),'tag','NumberToNextBest');
xlabel('Number of New Best Fval Found');
ylabel('Log Number of Local Solver Runs');
title('Number of Local Solver Runs to Find Lower Minimum')
case 'iter'
% Find the axes containing the histogram.
NumToNext = ...
findobj(get(gca,'Children'),'Tag','NumberToNextBest');
% Update the counter that records number of local
% solver runs to find next best minimum.
if ~isequal(optimValues.bestfval, bestfv)
bestfv = optimValues.bestfval;
bestcounter = [bestcounter 1];
else
bestcounter(end) = bestcounter(end) + 1;
end
% Update the histogram.
set(NumToNext,'Ydata',log(bestcounter))
end
Create the problem structure and global solver object. Set lower bounds of [-3e3,-4e3], upper bounds of [4e3,3e3] and set the global solver to use the NumberToNextBest custom plot function and the gsplotbestf built-in plot function.
problem = createOptimProblem('fmincon',... 'objective',@(x)sawtoothxy(x(1),x(2)),... 'x0',[100,-50],'lb',[-3e3 -4e3],... 'ub',[4e3,3e3],'options',... optimoptions(@fmincon,'Algorithm','sqp')); ms = MultiStart('PlotFcn',{@NumberToNextBest,@gsplotbestf});
Run the global solver for 100 local solver runs.
rng(2); % For reproducibility
[x,fv] = run(ms,problem,100);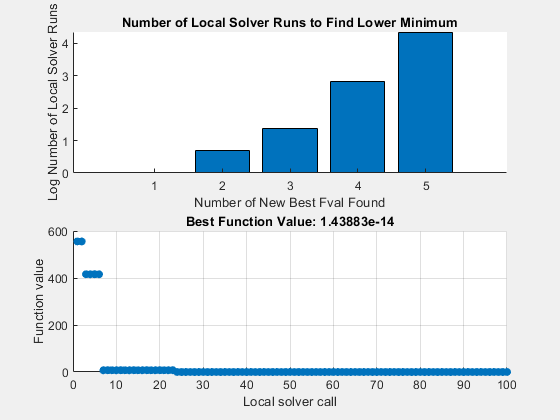
MultiStart completed some of the runs from the start points. 36 out of 100 local solver runs converged with a positive local solver exitflag.
Helper Functions
This code creates the sawtoothxy helper function.
function f = sawtoothxy(x,y) [t,r] = cart2pol(x,y); % change to polar coordinates h = cos(2*t - 1/2)/2 + cos(t) + 2; g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ... .*r.^2./(r+1); f = g.*h; end
No Parallel Plot Functions
While MultiStart can run in parallel, it does
not support global output functions and plot functions in parallel.
Furthermore, while local output functions and plot functions run on
workers when MultiStart runs in parallel, the effect
differs from running serially. Local output and plot functions do
not create a display when running on workers. You do not see any other
effects of output and plot functions until the worker passes its results
to the client (the originator of the MultiStart parallel
jobs).
For information on running MultiStart in parallel,
see Parallel Computing.