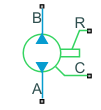
Fixed-Displacement Pump (2P)
Libraries:
Simscape /
Fluids /
Two-Phase Fluid /
Fluid Machines
Description
The Fixed-Displacement Pump (2P) block represents a pump that extracts power from a mechanical rotational network and delivers it to a two-phase fluid network. The pump displacement is fixed at a constant value that you specify through the Displacement parameter.
Ports A and B represent the pump inlets. Ports R and C represent the drive shaft and case. During normal operation, the pressure gain from port A to port B is positive if the angular velocity at port R relative to port C is positive.
The Fixed-Displacement Pump (2P) block assumes that liquid enters the pump inlet. You can use the Report when fluid is not fully liquid parameter to choose what the block does when the fluid does not meet liquid conditions. To move vapor in a two-phase fluid network, use a compressor.
Operating Modes
The block has four modes of operation, as shown by this image.
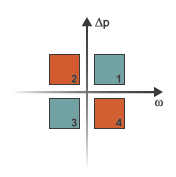
The working mode depends on the pressure gain from port A to port B, Δp = pB – pA and the angular velocity, ω = ωR – ωC:
The quadrant labeled 1 represents the forward pump mode. In this mode, the positive shaft angular velocity causes a pressure increase from port A to port B and flow from port A to port B
The quadrant labeled 2 represents the reverse motor mode. In this mode, the flow from port B to port A causes a pressure decrease from B to A and negative shaft angular velocity.
The quadrant labeled 3 represents the reverse pump mode. In this mode, the negative shaft angular velocity causes a pressure increase from port B to port A and flow from port B to port A
The quadrant labeled 4 represents the forward motor mode. In this mode, the flow from port A to port B causes a pressure decrease from A to B and positive shaft angular velocity.
The response time of the pump is negligible in comparison with the system response time. The pump reaches steady state nearly instantaneously and is treated as a quasi-steady component.
Energy Balance
The block associates the mechanical work done by the pump with an energy exchange. The governing energy balance equation is
where:
ΦA and ΦB are the energy flow rates at ports A and B, respectively.
Phydro is the pump hydraulic power, which is a function of the pressure difference between the pump ports: .
The block generates mechanical power due to torque, τ, and angular velocity, ω:
Flow Rate and Driving Torque
The mass flow rate generated at the pump is
where:
is the actual mass flow rate.
is the ideal mass flow rate.
is the internal leakage mas flow rate.
The driving torque required to power the pump is
where:
τ is the actual driving torque.
τIdeal is the ideal driving torque.
τFriction is the friction torque.
The ideal mass flow rate is
and the ideal required torque is
where:
ρ is the average of the fluid densities at ports A and B.
D is the Displacement parameter.
ω is the shaft angular velocity.
Δp is the pressure gain from inlet to outlet.
Leakage and Friction Parameterization
You can parameterize leakage and friction analytically, by using tabulated efficiencies or losses, or by using input efficiencies or input losses.
When you set the Leakage and friction parameterization parameter
to Analytical, the leakage flow rate is
and the friction torque is
where:
KHP is the Hagen-Poiseuille coefficient for laminar pipe flows. The block computes this coefficient from the specified nominal parameters.
μ is the dynamic viscosity of the fluid, which is the average of the values at the ports.
KTP is the friction torque vs. pressure gain coefficient at nominal displacement, which the block determines from the Mechanical efficiency at nominal conditions parameter, ηm:
τfr,nom is the friction torque at nominal conditions:
ΔpNom is the value of the Nominal pressure gain parameter. This value is the pressure gain at which the nominal volumetric efficiency is specified.
τ0 is the value of the No-load torque parameter.
ωNom is the value of the Nominal shaft angular velocity parameter.
The block determines the Hagen-Poiseuille coefficient from the nominal fluid and component parameters
where:
ωNom is the value of the Nominal shaft angular velocity parameter. This value is the angular velocity at which the block specifies the nominal volumetric efficiency.
μNom is the value of the Nominal Dynamic viscosity parameter. This value is the dynamic viscosity at which the block specifies the nominal volumetric efficiency.
ηv,Nom is the value of the Volumetric efficiency at nominal conditions parameter. This is the volumetric efficiency that corresponds to the specified nominal conditions.
When you set the Leakage and friction parameterization parameter
to Tabulated data - volumetric and mechanical efficiencies, the
leakage flow rate is
and the friction torque is
where:
α is a numerical smoothing parameter for the motor-pump transition.
is the leakage flow rate in motor mode.
is the leakage flow rate in pump mode.
τFriction,Motor is the friction torque in motor mode.
τFriction,Pump is the friction torque in pump mode.
This hyperbolic function describes the smoothing parameter α
where:
ΔpThreshold is the value of the Pressure gain threshold for motor-pump transition parameter.
ωThreshold is the value of the Angular velocity threshold for motor-pump transition parameter.
The block calculates the leakage flow rate from the volumetric efficiency, which the Volumetric efficiency table parameter specifies over the Δp–ɷ domain. When operating in pump mode, the leakage flow rate is:
where ηv is the volumetric efficiency, which the block obtains either by interpolation or extrapolation of the tabulated data. Similarly, when operating in motor mode, the leakage flow rate is:
The block calculates the friction torque from the mechanical efficiency, which the Mechanical efficiency table parameter specifies over the Δp–ɷ domain. When operating in pump mode, the friction torque is
where ηm is the mechanical efficiency, which the block obtains either by interpolation or extrapolation of the tabulated data. Similarly, when operating in motor mode, the friction torque is
When you set the Leakage and friction parameterization parameter
to Tabulated data - volumetric and mechanical losses, the block
specifies the leakage volumetric flow rate in tabulated form over the
Δp–ɷ domain:
The block calculates the mass flow rate due to leakage from the volumetric flow rate:
The block calculates the friction torque in tabulated form:
where qLeak(Δp,ω) and τLoss(Δp,ω) are the volumetric and mechanical losses, specified through interpolation or extrapolation of the tabulated data in the Volumetric loss table and Mechanical loss table parameters.
When you set the Leakage and friction parameterization parameter
to Input signal - volumetric and mechanical efficiencies, the
leakage flow rate and friction torque calculations are identical to the
Tabulated data - volumetric and mechanical efficiencies
setting. The block replaces the volumetric and mechanical efficiency lookup tables with
the physical signal input ports EV and
EM.
The efficiencies are positive quantities with values between 0 and
1.The block sets input values outside of these bounds to
0 for inputs smaller than 0 or
1 for inputs greater than 1. The block saturates
the efficiency signals at the value of the Minimum volumetric
efficiency or Minimum mechanical efficiency parameter
and the Maximum volumetric efficiency or Maximum mechanical
efficiency parameter.
When you set the Leakage and friction parameterization parameter
to Input signal - volumetric and mechanical losses, the leakage
flow rate and friction torque calculations are identical to the Tabulated
data - volumetric and mechanical efficiencies setting. The block replaces
the volumetric and mechanical loss lookup tables with the physical signal input ports
LV and LM.
The block expects the inputs to be positive and sets the signs automatically from the Δp–ɷ quadrant where the component is operating. If you provide a negative signal, the block returns zero losses.
Faults
To model a fault, in the Faults section, click the Add fault hyperlink next to the fault that you want to model. Use the fault parameters to specify the fault properties. For more information about fault modeling, see Introduction to Simscape Faults.
You can model a displacement fault, leakage, or a shaft friction torque fault.
When you enable the Displacement fault parameter, the block scales the displacement by the value of the Faulted displacement factor parameter when the fault triggers,
where fD is the value of the Faulted
displacement factor parameter. When the Leakage and friction
parameterization parameter is Analytical, the
block does not use the faulted displacement value to calculate the Hagen-Poiseuille
coefficient or the friction torque at nominal conditions.
When you enable the Leakage fault parameter and Leakage and
friction parameterization is Analytical,
Tabulated data - volumetric and mechanical efficiencies, or
Input signal - volumetric and mechanical efficiencies, the
faulted volumetric efficiency is
where fLeak is the value of the
Faulted leakage factor parameter and
ηv is the volumetric efficiency. When
Leakage and friction parameterization is
Analytical, the block uses the faulted volumetric efficiency
to calculate the Hagen-Poiseuille coefficient.
When Leakage and friction parameterization is Tabulated data
- volumetric and mechanical losses or Input signal -
volumetric and mechanical losses, the faulted leakage volumetric flow rate
is
When you enable the Shaft friction torque fault parameter and
Leakage and friction parameterization is
Analytical, Tabulated data - volumetric and
mechanical efficiencies, or Input signal - volumetric and
mechanical efficiencies, the faulted mechanical efficiency is
where fFriction is the value
of the Faulted shaft friction torque factor parameter and
ηm is the mechanical efficiency. When
Leakage and friction parameterization is
Analytical, the block uses the faulted mechanical efficiency
to calculate the friction torque at nominal conditions.
When Leakage and friction parameterization is Tabulated data
- volumetric and mechanical losses or Input signal -
volumetric and mechanical losses, the faulted friction torque is
Assumptions and Limitations
The block treats the pump as a quasi-steady component.
The block ignores the effects of fluid inertia and elevation.
The pump wall is rigid.
The block ignores external leakage.